Известен ряд способов для диагностирования такого сложного повреждения, как витковое замыкание в обмотке возбуждения синхронной машины (СМ), основанных на наличии связи между током возбуждения и величиной реактивной мощности обмотки статора [1, 2]. Главным недостатком таких способов является повышенная трудоемкость расчетов поправочных коэффициентов вследствие изменения теплового состояния машины при определении разницы между расчетным и фактическим значением тока возбуждения.
В то же время, если применить ряд системных позиций теории идентификации сложных динамических объектов [3], где в качестве настраиваемой модели применить так называемую модель типа «чёрный ящик», то это значительно усовершенствует методы диагностирования, основанные на анализе токов и напряжений статора. В отличие от классической теории описания работы электрической машины, в таких моделях отсутствуют строгие требования к явному математическому описанию системой дифференциальных или разностных уравнений динамики наблюдаемого объекта [4].
Цель исследования – доказать принципиальную возможность определения количества замкнувшихся витков обмотки возбуждения синхронной машины диагностической системой на основе нейро- эмулятора, определиться со стратегией его обучения и экспериментально проверить работоспособность и чувствительность системы к исследуемому повреждению.
За основу диагностической системы была принята динамическая искусственная нейронная сеть (ДНС) с задержкой по входу на один такт, поскольку такие ДНС помимо того, что способны запоминать предысторию процесса, а затем его прогнозировать, довольно просты в реализации. Для корректной работы таких ДНС необходимо согласовать частоты дискретизации и время задержки. Поскольку характерной особенностью при разработке ДНС является использование эмпирических знаний разработчика и при решении одной задачи у двух независимо работающих над ней исследователей будут решения, отличающиеся множеством деталей, существенным является описание решаемых задач разработки ДНС. При разработке ДНС для системы диагностики обмотки возбуждения СМ необходимо было выполнить следующие задачи:
– обосновать количество переменных подаваемых на вход ДНС;
– определиться с глубиной задержки подаваемых сигналов;
– определиться с типом функции активации нейронов скрытого слоя и с количеством слоев и нейронов в каждом скрытом слое;
– сформировать структуру ДНС в виде направленного графа и сделать математическое описание зависимости «вход – выход» как это принято в теории автоматического управления;
– разработать универсальную блочно-модульную структуру ДНС и обучить ее;
– проверить работоспособность системы при отсутствии и наличии различного количества замкнутых витков в обмотке возбуждения СМ и в различных режимах работы машины.
Формирование вектора входных сигналов нейроэмулятора
ДНС представляет собой универсальный аппроксиматор, который в случае наличия физически обусловленной неявно выраженной связи между векторами входных выходных сигналов обязательно ее выявляет [5].
Из теории электрических машин [6] известно, что изменение ЭДС статора пропорционально МДС индуцируемой обмотке возбуждения F = I?w A?вит, следовательно, изменение числа витков обмотки ротора (как и изменение тока возбуждения) должно привести к изменению ЭДС статора и также реактивной мощности машины. Взяв за основу эти физически обусловленные предпосылки, авторы пришли к следующему утверждению – для правильной работы ДНС достаточно, если на входном слое нейросети будут поданы мгновенные значения сигналов: напряжения и тока обмотки ротора, проекции в двухфазной неподвижной системе координат векторов тока и напряжения статора, значения реактивной мощности, а также задержки всех этих сигналов.
Выбор глубины задержки входных сигналов
Введение задержек превращает нейронную сеть в динамическую нейронную сеть [7], способную работать с динамически работающими объектами, каким и является синхронный генератор. Исходя из ограничений, накладываемых аппаратной частью экспериментальной установки, собранной из элементной базы, принятой в релейной защите и автоматике – верхняя граница частоты дискретизации 2400 Гц авторами была принята задержка входных сигналов Δtзадер = 500 мкс.
Определение типа функции активации, числа скрытых слоев и нейронов в скрытых слоях
Исходя из рекомендаций, изложенных в [8], авторами решено использовать в качестве функции активации нейронов скрытых слоев функцию гиперболического тангенса th(x).
Несмотря на то, что с увеличением количества скрытых слоев мощность и аппроксимирующая способность нейросети увеличивается, необходимо учесть резкие затраты времени и сложность обучения. На практике в ДНС количество слоев следует брать минимальным. Авторами принята структура ДНС с двумя скрытыми слоями, в первом скрытом слое – 35 нейронов, во втором слое – 25 нейронов.
Структура разработанной нейросети в виде направленного графа и математическое описание «вход – выход»
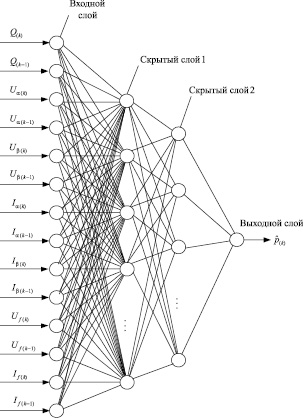
Рис. 1. Структура разработанной ДНС
На рис. 1 приведена структура разработанной ДНС. Математически зависимость «вход – выход» ДНС (рис. 1) определяется как мгновенная величина оценки процента 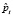 замкнувшихся витков обмотки возбуждения СМ по формуле
замкнувшихся витков обмотки возбуждения СМ по формуле
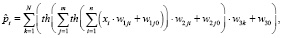
где N – число нейронов во втором скрытом слое; m – число нейронов в первом скрытом слое; n – число нейронов во входном слое; w1ji – синаптический вес i-го входа j-го нейрона первого скрытого слоя; w1j0 – сдвиг j-го нейрона первого скрытого слоя; w2ji – синаптический вес i-го входа j-го нейрона второго скрытого слоя; w2j0 – сдвиг j-го нейрона второго скрытого слоя; w3j – синаптический вес k-го входа нейрона выходного слоя; w30 – сдвиг нейрона выходного слоя; xi – входные сигналы ДНС.
Обучение ДНС
Обучение ДНС для системы диагностики синхронной машины является сложной и трудоемкой задачей, поскольку требуется либо большая база экспериментальных данных, снятых в различных режимах работы машины, либо в качестве объекта наблюдения использовать адекватную математическую модель синхронной машины. Подход к построению системы диагностики СМ заключается в том, что вход СМ и на вход ДНС поступает одинаковый вектор входных параметров u, под воздействием которого происходит изменение компонент вектора х переменных состояний СМ. Векторы х и u формируют вектор у измеряемых переменных СМ и вектор 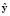 , рассчитываемый оценка переменных состояний
, рассчитываемый оценка переменных состояний 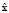 наблюдателя. Сравнив векторы у и
наблюдателя. Сравнив векторы у и 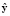 , получают вектор невязки
, получают вектор невязки 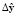 . Затем определяется целевая функция ошибки наблюдения
. Затем определяется целевая функция ошибки наблюдения 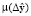 . Минимизировав
. Минимизировав 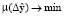 , находим оптимальный вектор
, находим оптимальный вектор  параметров ДНС. Такой подход достаточно универсален, поскольку возможна настройка системы на различные виды СМ. Недостатком же является то, что из-за принимаемых допущений возникают дополнительные трудности в некоторых специфических режимах работы СМ. На рис. 2 показана разработанная авторами структура системы для настройки диагностической системы, в которой имеется ДНС в качестве настраиваемой модели. Объектом наблюдения при обучении ДНС выступает дискретная математическая модель СМ с витковым замыканием в обмотке ротора. В этой конфигурации диагностической системы невязка
параметров ДНС. Такой подход достаточно универсален, поскольку возможна настройка системы на различные виды СМ. Недостатком же является то, что из-за принимаемых допущений возникают дополнительные трудности в некоторых специфических режимах работы СМ. На рис. 2 показана разработанная авторами структура системы для настройки диагностической системы, в которой имеется ДНС в качестве настраиваемой модели. Объектом наблюдения при обучении ДНС выступает дискретная математическая модель СМ с витковым замыканием в обмотке ротора. В этой конфигурации диагностической системы невязка 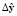 определяется как разница между задаваемым значением замкнувшихся витков ε и её оценкой
определяется как разница между задаваемым значением замкнувшихся витков ε и её оценкой 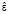 , вычисленной ДНС. Целевая функция ошибки обучения ДНС
, вычисленной ДНС. Целевая функция ошибки обучения ДНС 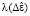 минимизируется
минимизируется 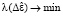 одним из методов глобальной оптимизации и находится оптимальный вектор w весов.
одним из методов глобальной оптимизации и находится оптимальный вектор w весов.
Рис. 2. Структура системы для настройки ДНС
Несмотря на то, что в качестве источника данных об объекте выступает не реальная машина, а специально разработанная дискретная модель, это не наносит влияния на качество обучения ДНС, так как саму диагностическую систему можно легко дообучить известным методом подкрепляемого обучения [9].
Наилучшим алгоритмом обучения из числа проверенных авторы посчитали алгоритм Левенберга – Марквардта, поскольку он сочетает в себе как алгоритм Ньютона, так и алгоритм наискорейшего градиентного спуска.
Само обучение ДНС заключается в нахождении минимума функции f(x) на множестве допустимых решений. Методом Левенберга – Марквардта задача решается построением последовательности точек  чтобы
чтобы  . Сами точки вычисляются следующим образом:
. Сами точки вычисляются следующим образом:
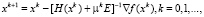
где x0 задается расчетчиком, E – единичная матрица, μk – последовательность положительных чисел.
Задача считается решенной, если в точке xk выполняется условие 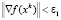 , или же k ≥ N, где ε1 – заданная точность расчета, а N – число итераций.
, или же k ≥ N, где ε1 – заданная точность расчета, а N – число итераций.
Надо признать, что процесс обучения ДНС данным методом требует, по сравнению с другими методами, значительно больших вычислительных ресурсов компьютера.
Результаты исследования и их обсуждение
Результаты экспериментальной проверки на ГАБ-4-Т/230
|
Активная мощность, Вт |
Реактивная мощность, ВА |
Ток возбуждения, А |
Количество замкнутых витков, шт ( %) |
Количество замкнутых витков, шт ( %) |
Процент ошибки, % |
|
1615 |
785 |
6,1 |
9 (3,6) |
10 (4) |
0,4 |
|
1604 |
640 |
6,45 |
18 (7,2) |
20,5 (7,6) |
1 |
|
1605 |
537 |
7 |
37 (14,8) |
39 (15,6) |
0,8 |
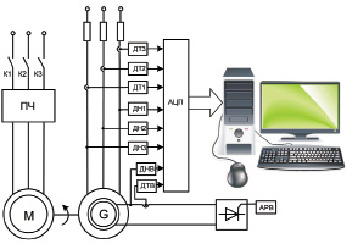
Рис. 3. Принципиальная схема экспериментальной установки: ДН1-3 – датчики напряжения статора, ДТ1-3 – датчики тока статора, ДНВ, ДТВ – датчики напряжения и тока возбуждения, М – приводной двигатель, G – генератор ГАБ-2-Т/230, ПЧ преобразователь частоты, АРВ – автоматический регулятор возбуждения
Для проверки работоспособности системы диагностики виткового замыкания в обмотке возбуждения СМ была создана экспериментальная установка, объектом наблюдения в которой был синхронный генератор ГАБ-2-Т/230. На рис. 3 показана принципиальная схема экспериментальной установки. Сигналы с датчиков тока и напряжения обмотки возбуждения, расчетные значения реактивной мощности и проекции в двухфазной неподвижной системе координат векторов тока и напряжения статора, а также задержки всех этих сигналов подавались на вход заранее обученной ДНС. Задержка по времени составила 0,5 мс. Величина оценки числа замкнувшихся витков 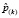 в процентах отображалась на мониторе.
в процентах отображалась на мониторе.
Правильность работы ДНС проверялась тестирующей выборкой, данные которой не отсутствовали в тренировочном наборе. В процессе обучения ДНС число замкнувшихся витков было: wкз = 0 %, wкз = 3,66 %, wкз = 7,2 %, wкз = 14,8 %, а в тестирующей выборке wкз=12 %.
Как показала проверка ДНС оказалась работоспособной и негативный эффект переобучения отсутствовал.
Результаты экспериментальной проверки работоспособности ДНС приведены в таблице.
Выводы
Результаты исследования, приведенные в статье, позволяют сделать вывод о том, что цель исследования была достигнута, а именно, доказана принципиальная возможность определения доли замкнутых витков обмотки возбуждения синхронной машины на основе разработанной авторами динамической нейронной сети.
Экспериментально доказано, что чувствительность диагностической системы к витковым замыканиям в обмотке возбуждения составила 2,5…2,7 % от общего количества витков.



