В настоящей статье изложены некоторые результаты, полученные при решении комплексной задачи по оценке прочности и долговечности плоской стальной пластины с учетом необратимых деформаций, повреждаемости ее материалов при ползучести, а также водородной коррозии при высоких температурах. Для выполнения расчетов применялась методика прочностного расчета пластин и оболочек, разработанная авторами, описание которой изложено в работах [1, 2] и в ряде других публикаций.
Для учета влияния деградации структуры материалов при ползучести на процесс деформирования пластины используется традиционный подход, который заключается в использовании числового (скалярного) параметра повреждаемости, вводимого в расчетные соотношения. Вычисление этого параметра выполняется с помощью кинетического уравнения повреждаемости Ю.Н. Работнова, которое неоднократно использовалось при решении многих аналогичных задач, таких как [3–5]. Для учета влияния коррозионного воздействия высокотемпературного водорода на процесс деформирования конструкции любого типа может быть использован какой-либо из подходов, подробно рассмотренных в монографии [6]. Примерами практического применения этих подходов к прочностным расчетам пластин и оболочек являются работы [7–9]. В работе [10] показан пример использования одной из известных моделей такого типа к исследованию влияния воздействия высокотемпературного водорода на поведение металлов и некоторых видов конструкций, а в работе [11] – пример применения программного комплекса ANSYS к решению аналогичных задач.
Таким образом, к настоящему времени разрушающее воздействие водорода на большинство видов малоуглеродистых сталей изучено достаточно подробно и на эту тему опубликовано большое количество исследовательских и обзорных научных работ. В них говорится, что воздействие водорода высоких параметров (давления и температуры) приводит к значительному ухудшению пластических и прочностных свойств большинства конструкционных сталей, что в конечном итоге способствует их охрупчиванию [6].
Однако в настоящее время практически нет публикаций, в которых была бы рассмотрена возможность совместного учета повреждаемости материалов, вызванных водородной коррозией и температурной ползучестью. Таким образом, главной задачей исследований, частью которых является настоящая работа, является определение условий, которые приводят к деградации механических характеристик материалов вследствие водородной коррозии, а также определение степени этой деградации.
Целью исследования является описание некоторых наиболее известных подходов, применяемых для учета влияния коррозионного воздействия высокотемпературного водорода на процесс деформирования машиностроительных конструкций, и их практическое применение для расчета реальных объектов.
Далее подробно рассмотрим эти подходы.
Материалы и методы исследования
Обобщенная модель химического взаимодействия
Данная модель строится в предположении, что разрушающее воздействие водородосодержащей среды на конструкционные стали проявляется не сразу, а по прошествии некоторого отрезка времени, получившего название инкубационный период tинк, продолжительность которого в общем случае зависит от давления водорода, температуры, вида напряженного состояния и некоторых других факторов. После завершения этого периода происходит интенсивное вытеснение свободного углерода (обезуглероживание) из материала конструкции, приводящее к деградации (довольно часто существенной) его механических характеристик. Период времени, в течение которого происходит обезуглероживание материала конструкции, называется периодом активных химических превращений tкр. В результате многочисленных экспериментов установлено, что деградация механических свойств материалов происходит только в течение этого периода и только до определённого предельного состояния, которое всегда является конечным и не зависит от давления водорода, температуры и вида напряженного состояния [6].
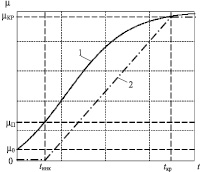
Рис. 1. Зависимость параметра химического воздействия водорода от времени
Для описания процесса воздействия высокотемпературного водорода на свойства материала применяется дифференциальное уравнение, позволяющее определить степень поражения материала водородной коррозией, для количественного описания которой вводится скалярный параметр μ, изменяющийся от начального значения μ0 > 0 до конечного μКР < 1:
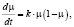 (1)
(1)
где k(p, T, ωC) – функция, которая позволяет определить зависимость, параметра μ от температуры T, давления p и степени поврежденности ωC материала.
Более подробно данная модель, а также способы ее конкретизации описаны в публикации авторов [2], а также в монографии [6].
В результате решения дифференциального уравнения (1) получается логистическая функция Ферхюльста, график которой приведен на рис. 1 под номером 1. Значения tинк, tкp и их связь с параметром μ показаны на графике.
Функция Ферхюльста для решения поставленной задачи выглядит следующим образом:
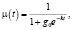 (2)
(2)
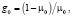 (3)
(3)
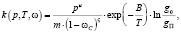 (4)
(4)
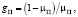 (5)
(5)
где m, u, B, ζ, μ0, μП – некоторые константы, которые могут быть получены в результате натурных экспериментов. Один из вариантов методики проведения таких экспериментов изложен в работе [6].
Кроме этого, значительное влияние на скорость процесса поражения материала водородной коррозией оказывает вид напряженного состояния, для учета влияния которого используется следующая зависимость коэффициента m от σ:
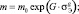
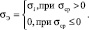 (6)
(6)
Здесь g, G, m0 – эмпирические константы; σЭ – эквивалентное напряжение, σср – среднее напряжение, σi – интенсивность напряжений.
Упрощенная модель химического взаимодействия
Данная модель основана на ранее рассмотренной обобщенной модели и предполагает, что «при t < tинк изменений механических свойств материалов еще не происходит, а при t > tкp уже не происходит» [6]. Такое упрощение позволяет отказаться от использования функции Ферхюльста и заменить ее тремя отрезками прямых линий (график 2 на рис. 1). В результате параметр μ будет изменяться от 0 до 1 и описываться следующей параметрической функцией:
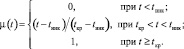 (7)
(7)
Для вычисления данной функции требуется определить значения инкубационного периода и периода активных химических превращений. Для их определения используются следующие соотношения [6]:
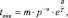 (8)
(8)
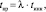 (9)
(9)
где p – значение парциального давления водорода, МПа;
T – значение температуры;
m, u, B – константы материала, определяемые в результате натурных экспериментов;
λ – параметр, с помощью которого определяется, во сколько раз продолжительность инкубационного периода меньше периода изменений механических свойств материалов.
В некоторых случаях (например, если длительность периода активных химических превращений значительно меньше полного времени нагружения конструкции), можно заменить обобщенную или упрощенную модели химического взаимодействия ступенчатой функцией, которая будет эквивалентна мгновенному переходу свойств материала из исходного состояния в обезуглероженное. В ранее опубликованных работах авторов (например, [1, 2]) было показано, что такое упрощение практически не влияет на конечный результат оценки времени до разрушения конструкции.
Учет влияния вида напряженного состояния на скорость коррозии осуществляется аналогично обобщенной модели.
Давление водорода распределяется по толщине неравномерно, и вычисляется следующим образом [6]:
в случае плоской пластины:
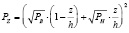 , (10)
, (10)
в случае оболочки со сложной формой меридиана:
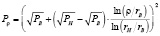 , (11)
, (11)
где ρ – сферическая координата; z – плоская координата; h – толщина пластины или оболочки; rH – значение внешнего радиуса оболочки; rB – значение внутреннего радиуса оболочки; PH – наружное давление; PB – внутреннее давление.
Более подробное описание рассмотренных, а также других моделей воздействия водородосодержащей среды на материалы конструкции приведены в работе [6]. В данной публикации упомянуты только те модели, которые были использованы авторами в составе разработанного ими программного комплекса [1, 2]. В этих публикациях также описан и алгоритм учета влияния водорода на прочностные свойства конструкции.
Результаты исследования и их обсуждение
В качестве примера рассмотрим результаты расчета напряженно-деформированного состояния равномерно нагретой двух- и трехслойной кольцевой пластины с круглым отверстием, находящейся под давлением высокотемпературного водорода. Геометрические размеры пластины следующие: R = 110 мм, r = 65 мм, δ = 10 мм (рис. 2). В трехслойной пластине центральный слой выполнен из стали марки 20, а верхний и нижний – из материала 12X18H9T, в двухслойной – материал 12X18H9T располагается сверху.
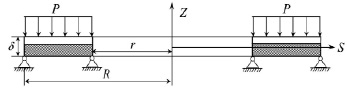
Рис. 2. Осевое сечение пластины
Давление водорода осуществляется со стороны верхнего слоя пластины и является постоянным во времени, а внутренний и наружный кольцевые контуры закреплены шарнирно – неподвижно. Константы, определяющие свойства материала в соотношениях (2) и (3), были взяты из [6], которые для материала сталь 20 и рассматриваемых условий нагружения равны: u = 1,73; B = 13500; λ = 5. Используя результаты работы [6], допускается предположить, что при данных условиях нагружения воздействие высокотемпературного водорода практически не оказывает влияние на механические свойства сплава 12X18H9T. Расчеты проводились с использованием упрощенной модели химического взаимодействия и без учета влияния вида напряженного состояния на процесс развития водородной коррозии, поскольку для этого требуются дополнительные исследования [1].
В ранее опубликованных работах [1, 2] авторами было исследовано напряженно-деформированное состояние одно- и двухслойных пластин с учетом ползучести и высокотемпературной водородной коррозии. В данной публикации проведем аналогичное исследование трехслойной пластины, имеющей такие же размеры, и сравним его результаты с ранее полученными для двухслойной пластины.
В ходе исследований требовалось определить влияние защитного слоя 12X18H9T определенной толщины на время до разрушения пластины при различных значениях давлений водорода. На основе полученных результатов расчетов требовалось построить графики распределения деформаций, напряжений, зон повреждаемости и пластичности в отдельные моменты времени в начале процесса нагружения, перед разрушением и сразу после него. Некоторые наиболее важные результаты показаны на рис. 3–6.
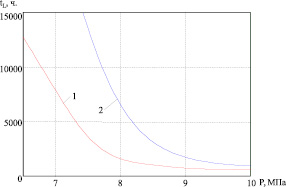
Рис. 3. Зависимость времени разрушения пластин от времени
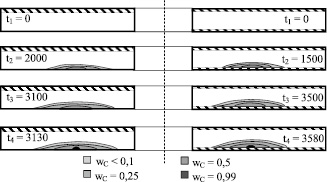
Рис. 4. Разрезы осевого сечения пластин в различные моменты времени
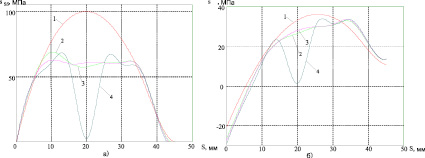
Рис. 5. Меридиональные и окружные напряжения для двухслойной пластины
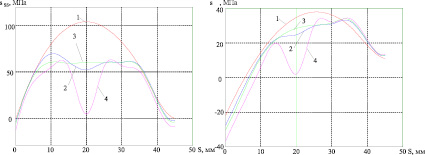
Рис. 6. Меридиональные и окружные напряжения для трехслойной пластины
На рис. 3 приведены кривые, отражающие зависимость времени до разрушения от давления водорода, кривая 1 – двухслойная пластина, кривая 2 – трехслойная.
На рис. 4 изображено осевое сечение пластины в разрезе, на котором показаны четыре уровня поврежденности материала (для этого была использована заливка области с соответствующей степенью поврежденности серым цветом определенной яркости), зафиксированные в определенные моменты времени (в начале процесса нагружения, в середине, перед разрушением и после него). В левой половине рисунка приведены результаты, полученные для двухслойной пластины (эти результаты были приведены авторами в предыдущих работах, в частности [1]), на правой части – результаты, полученные для трехслойной пластины. Указанные моменты времени для каждой из пластин подбирались таким образом, чтобы характер распределения зон повреждаемости для них был примерно одинаковым. При этом трехслойная пластина оказывается в аналогичном состоянии через более длительное время, чем двухслойная, что говорит о том, что введение третьего слоя позволяет увеличить время до разрушения пластины. Также следует отметить, что области, в которых зафиксирована поврежденность материала, всегда располагаются в слое с малоуглеродистой сталью.
На рис. 5 изображены меридиональные (а) и окружные (б) напряжения, действующие на нижней поверхности двухслойной пластины, которые получены для тех же самых моментов времени, что и на рис. 4, а на рис. 6 – аналогичные графики для трехслойной пластины.
Выводы
Полученные результаты в целом позволяют сделать вывод о том, что трехслойная пластина при одинаковых внешних условиях более долговечна, чем двухслойная, толщина защитного слоя в которой равна сумме толщин защитных слоев в трехслойной пластине.



