Начиная с 2002–2003 гг. авторами данной статьи [1] теоретически и практически развивалась инновационная сервисная методология по отношению к процессу обучения математике, информатике и информационным технологиям (ИТ) в высшей школе. В качестве основы этой методологии был предложен новый педагогический термин – сервис обучения (СО). К настоящему времени разработаны десятки СО, которые внедрены в практику обучения студентов нескольких вузов Санкт-Петербурга в качестве эксперимента. Этот многолетний эксперимент убедительно продемонстрировал существенное улучшение качества обучения благодаря применению СО.
Приблизительно с 2004 г. в ряде научных публикаций [2–4], посвященных таким областям знаний, как экономика, информатика, информационные технологии (ИТ), педагогические технологии (ПТ), авторы говорят о фактическом возникновении новой науки – науки о сервисах, управлении и инжиниринге, по-английски – Service Science, Management and Engineering (SSME). Термин SSME предложен исследовательским центром IBM [1; 4] как название новой науки, включающей в себя, в частности, и Computer Science, известную в России как информатика. Интересно, что термин Computer Science в середине ХХ века также был предложен IBM. Информатика до последнего времени рассматривалась как универсальная наука, обслуживающая другие науки, что делало ее похожей на математику и философию. Теперь аналитики IBM считают науку о сервисах (SSME) еще более универсальной наукой, а сервисы – универсальными продуктами науки, искусства, промышленности. Указанные обстоятельства подтверждают перспективность работы авторов статьи по развитию сервисной методологии обучения.
Психолого-педагогические аспекты проблемы
Исследовательским центром IBM [3; 4] отмечается отсутствие общего определения понятия сервиса, необходимого для фундаментальных научных исследований в SSME. Приведем определение СО, принадлежащее авторам статьи. Оно может быть легко распространено на более общий случай. Предположим, что в процессе обучения возникает некоторая задача P. Под сервисом обучения S мы будем понимать [1; 5] набор из такой задачи P и непустого множества M ее решений Ri, где непустое множество M состоит из одного или нескольких элементов.
S = (P, M), где M = {R1} или M = {R1, R2...}. (1)
Решением возникающей в процессе обучения задачи P мы будем называть некоторый подлежащий описанию механизм ее реализации, обладающий свойством повторяемости (технологию). В принципе, для реализации P достаточно одного механизма R1, но если преподаватель располагает несколькими механизмами R1, R2..., то возрастает надежность реализации P. Если при проведении занятия не сработает один механизм, то преподаватель сможет применить другой. Английское слово «service» переводится на русский язык как «служба». А служба означает многократную реализацию на протяжении длительного времени некоторой задачи. Такова, например, пожарная служба. В формуле (1) каждый механизм Ri – это набор из нескольких необходимых для реализации P компонент ri,k – формула
Ri = (ri,1; ri,2; ...). (2)
Эти компоненты ri,k могут быть как материальными, так и интеллектуальными, в частности – междисциплинарными. Часто перед вузом, кафедрой или отдельным педагогом ставится некоторая нетривиальная задача, причем ее решение ему не известно, но его необходимо оперативно найти и реализовать. Тогда фактически отдельным педагогом или некоторой рабочей группой педагогов и строится СО. Фиксация в рамках СО и задачи и найденных ее решений позволяет использовать СО неоднократно в аналогичных ситуациях. Опытный педагог отличается от неопытного, в частности, освоенным набором СО.
Наша статья [6] была посвящена некоторым практическим методам усиления мотивации студентов к обучению. Данная статья является ее продолжением и развитием на базе сервисной методологии обучения. В [6] решать проблему усиления мотивации студента, в частности, предлагалось применением теории деятельности [7] А.Н. Леонтьева и теории мотивации [8] А. Маслоу. Разработка соответствующих СО позволяет использовать творческие находки педагога [9; 10] не разово, а многократно в различных, но в чем-то подобных ситуациях. По А.Н. Леонтьеву, сфера мотивации человека есть образ его практической деятельности, и наоборот. Нужно стараться неосвоенные пока действия, имеющие у студента невысокую мотивацию, заменить хотя бы частично на уже освоенные действия, имеющие у студента высокую мотивацию. Например, теоретико-математические рассуждения по новому материалу часто можно заменить на решение заранее подобранной преподавателем последовательности практических задач. По А. Маслоу, существует иерархия человеческих потребностей, состоящая из шести уровней. Следует новый учебный материал как-то связать с потребностями, принадлежащими к начальным уровням, которые человек стремится удовлетворить в первую очередь.
Практические аспекты проблемы
В [6] рассказывалось о положительном практическом опыте авторов обучения студентов математическому и информационному моделированию физических механических явлений на примере моделирования выстрела из лука и арбалета. По А. Маслоу, мы при этом попадаем на уровень 1 с самой сильной мотивацией. Были даны математические модели выстрела из устройств 2 типов: 1) из блочного лука с падающей полочкой; 2) из блочного лука с волосяной полочкой и из любого арбалета, не обязательно блочного. Здесь в дополнение строится математическая модель выстрела из традиционного или классического лука. Если из математических моделей не следует никаких алгоритмов, то практическая их значимость находится под сомнением, тогда, по А.Н. Леонтьеву, мотивация студентов к изучению такого материала невысока. Здесь представлены соответствующие алгоритмы расчета скорости стрелы varr, для различных случаев, причем представлены 2 подхода к таким алгоритмам.
В [6] требуется, чтобы тетива при выстреле обязательно растягивалась до предела – таковы все блочные луки и все арбалеты. Традиционные и классические луки не таковы. Рисунок показывает зависимость силы натяжения от длины натяжения: А) для блочных луков; Б) для традиционных и классических луков. Кривая для блочного лука имеет 3 промежутка по S: 1) <0; S1>, 2) <S1; S2>, 3) <S2; Smax>, причем Fmax = F(S1), F(Smax) = Fres, Fres<<Fmax. – в результате прицеливание происходит на небольшом усилии (Fres) спортсмена. Кривая для традиционного или классического лука представляет собой растянутый первый промежуток <0; S1>, следовательно, S1 = Smax и F(Smax) = Fmax. – прицеливание происходит на максимальном усилии спортсмена. Аналогичные кривые характерны соответственно для блочных и неблочных арбалетов. Однако для всякого арбалета прицеливание происходит на нулевом усилии спортсмена – натянутую тетиву держит специальный замок. Можно ли пренебречь трением стрелы? В [6] рассматриваются оба случая. Для падающей полочки трением можно пренебречь, для всего остального – нельзя.
Подход на основе выстрелов
Этот подход основывается на самом простом эксперименте: производим из изучаемого лука или арбалета 2–3 выстрела различными по массе стрелами и замеряем скорости этих стрел. Используя эти данные и математическую модель, находим 2–3 ключевые характеристики конкретного устройства – лука или арбалета. Эти ключевые характеристики позволяют нам по любой массе стрелы аналитически определять ее скорость.
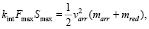 (3)
(3)
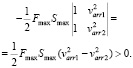 (4)
(4)
Для блочного лука с падающей полочкой формула (3) – следствие формул из [6]. Здесь: Fmax – максимальная сила натяжения тетивы; Smax – максимальная длина натяжения тетивы; kint – интегральный коэффициент данного устройства; varr – скорость вылета стрелы; marr – масса стрелы; mred – приведенная масса данного устройства, FmaxSmax – теоретически максимальная работа, которая может быть совершена спортсменом при натяжении тетивы, kintFmaxSmax – реальная работа спортсмена. Смысл формулы (3) прост: реальная работа спортсмена равна сумме кинетической энергии стрелы на вылете и кинетической энергии всех движущихся частей устройства. Рассмотрим величины kint, mred как неизвестные, а остальные – как известные. Получим линейное уравнение с 2 неизвестными. При фиксированных Fmax, Smax мы делаем 2 выстрела различными по массе стрелами marr1 < marr2, хронографом замеряем соответствующие скорости стрел, очевидно, получится, что varr1 > varr2. В результате мы получаем линейную систему 2 уравнений с 2 неизвестными с ненулевым (4) главным определителем. В результате ее решения мы находим неизвестные kint, mred. Зная эти величины и используя (3), для произвольной стрелы массой marr мы можем найти varr.
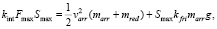 (5)
(5)
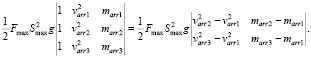 (6)
(6)
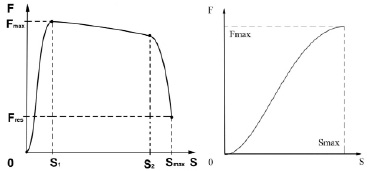
А) Б)
Зависимость силы натяжения (F) от длины натяжения (S): А) для блочных луков; Б) для традиционных и классических луков
Для блочного лука с волосяной полочкой и любого арбалета формула (5) – следствие формул из [6]. Здесь учитывается трение стрелы: kfri – коэффициент трения, g – ускорение свободного падения. Используем закон Амонтона – Кулона для трения стрелы. Смысл формулы (5): реальная работа спортсмена равна сумме кинетической энергии стрелы на вылете, кинетической энергии всех движущихся частей устройства и работы силы трения. Рассмотрим величины kint, mred, kfri как неизвестные, а остальные – как известные. Получим линейное уравнение с тремя неизвестными. При фиксированных Fmax, Smax мы делаем 3 выстрела различными по массе стрелами marr1 < marr2 < marr3, замеряем соответствующие скорости стрел, очевидно, получится, что varr1 > varr2 > varr3. В результате мы получаем линейную систему трех уравнений с тремя неизвестными. Ее главный определитель (6) может в принципе быть и нулевым, тогда придется брать другой набор стрел. При ненулевом главном определителе (6) мы находим неизвестные kint, mred, kfri. Зная эти величины и используя формулу (5), для произвольной стрелы массой marr мы можем найти varr.
Подход на основе кривой и выстрелов
На мысль об этом подходе нас навели видеолекции Андрея Шалыгина [11] по поводу сравнения традиционных луков между собой. По каждому луку он экспериментально строит кривую зависимости силы натяжения от длины натяжения – рисунок, Б, причем делает это достаточно просто, используя только линейку и фунтометр. Аналогично – для неблочного арбалета. Также легко может быть экспериментально построена и кривая для блочного лука или блочного арбалета (рисунок, А).
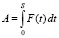 , где S∈[0; Smax]. (7)
, где S∈[0; Smax]. (7)
Формула (7) применима для традиционного или классического лука. Здесь A – работа спортсмена при длине натяжении тетивы S. На рисунке, Б – это площадь части подграфика. В [6] есть аналогичная формула для блочного лука и любого арбалета, там Smax – верхний предел интеграла. Легко при некотором фиксированном S численно определить A как интеграл от экспериментальной кривой – это относится к любым лукам и арбалетам.
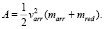 (8)
(8)
Формула (8) для блочного лука с падающей полочкой – аналог (3). Единственная неизвестная величина mred легко определяется после 1 выстрела.
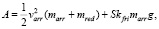 (9)
(9)
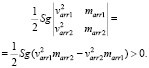 (10)
(10)
Традиционные и классические луки падающих полочек не имеют, поэтому здесь трением стрелы пренебрегать нельзя. Формула (9) – аналог (5), применима к устройствам, где трением стрелы пренебрегать нельзя. Для всех арбалетов и блочных луков с волосяными полочками для (9) считаем, что S = Smax. Для традиционных и классических луков для (9) считаем, что S имеет некоторое фиксированное значение. Формула (9) дает нам линейное уравнение относительно неизвестных mred и kfri. Мы делаем 2 выстрела различными по массе стрелами marr1 < marr2, замеряем соответствующие скорости стрел, очевидно, получится, что varr1 > varr2. В результате мы получаем линейную систему двух уравнений с двумя неизвестными с ненулевым (10) главным определителем. Решая систему, мы находим неизвестные.
Таким образом, в [6] и в данной статье представлены математические и алгоритмические модели выстрела из всех широко известных типов луков и арбалетов. Для развития таких исследований можно предложить 2 направления: 1) В зависимости от силы и длины рук спортсмена у блочного лука регулируются Fmax и Smax соответственно. Очевидно, kfri при этом никак не меняется. А как изменятся другие ключевые параметры kint и mdev блочного лука при изменении Fmax и Smax? Как изменится при этом кривая, представленная на рисунке, А? 2) На некоторых блочных арбалетах PSE [11] вместо стандартного ложа для стрелы используется волосяная полочка, как на блочных луках. За счет этого существенно уменьшается kfri, а значит – сила трения стрелы. В результате скорость стрелы увеличивается на 5–7 м/с по сравнению с обычными блочными арбалетами при аналогичных параметрах Fmax ≈ 80–90 кгс, Smax ≈ 30–40 см. А использование падающей полочки позволило бы уменьшить трение вообще до пренебрежимо малых величин! По сравнению с блочными арбалетами блочные луки имеют обычно большую Smax ≈ 60–80 см, но меньшую Fmax ≈ 24–36 кгс, иначе у спортсмена не хватит силы растягивать тетиву лука. На основании формул из [6] и данной статьи у авторов возникла мысль о создании гибрида «блочного лука-арбалета с падающей полочкой». Тогда мы получили бы Smax ≈ 80 см и Fmax ≈ 80–90 кгс. Следовательно, запасенная энергия возрастет приблизительно в 2 раза, а с учетом практического отсутствия трения скорость стрелы – приблизительно в 1,5 раза. Если сейчас она приблизительно 115– 130 м/с, то будет около 170–200 м/с. В такой конструкции целесообразно плечи расположить, как у лука, – вертикально, а тетиву натягивать до конца приклада, получится аналог ружья «буллпап». Размеры конструкции будут вполне приемлемыми: высота 60–80 см (из-за вертикальных плеч, как у лука); длина 80–90 см (из-за конструкции, аналогичной «буллпап»); ширина 8–10 см (из-за падающей полочки, оптического прицела, механического натяжителя и замка тетивы).
Заключение
Настоящая статья на основе психолого-педагогической науки, теории деятельности А.Н. Леонтьева, теории мотивации А. Маслоу, современной науки о сервисах (SSME), инновационной сервисной методологии педагогики, развиваемой авторами статьи, предлагает теорию построения усиливающих мотивацию студентов СО математике, информатике, математическому и информационному моделированию. Настоящая статья также дополняет статью [6] в смысле продолжения практического построения конкретного такого СО. Дополнена математическая модель, построена алгоритмическая модель. Построение информационной модели с использованием языка моделирования (UML, iDEF) на базе представленной алгоритмической модели не представляет труда.



