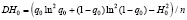Использование статистических методов для исследования и анализа промышленной продукции началось еще в XIX в. в Великобритании и других промышленно развитых странах. В конце XIX в. статистический подход к контролю и управлению начал разрабатывать великий российский ученый М.В. Остроградский.
Можно отметить, что именно статистические методы управления технологическим процессом позволили добиться невероятного повышения доли качественных (т.е. удовлетворяющих требованиям потребителя) изделий в общем потоке. Японское экономическое чудо, концепция «Шесть сигм», «Дао Тойота» и другие примеры дают основание утверждать о важности статистических методов исследования.
Следует заметить, что основные принципы контроля и управления качеством основаны на использовании больших выборок, исчисляющимися десятками, а то и тысячами.
В современном производстве, особенно в оборонной промышленности, когда работа ведется по заказам, согласно которым нужно произвести единицы изделий, такой подход становится неадекватным.
Решению этой проблемы посвящены, в частности, работы [1, 2].
Исследования авторов привели к выводу о необходимости разработки специальных методов контроля и управления качеством в случае мелкосерийного и штучного производства. В качестве методической базы предлагается использовать байесовский подход, применение которого описано в работах [1, 2], и методы математической теории информации, представленных в работах [3, 4].
Целью исследования предлагаемой к рассмотрению работы является попытка интеграции байесовского и информационно-статистического подхода к построению планов статистического приемочного контроля (СПК), в случае контроля партий малого объема.
Материалы и методы исследования
Теоретические основы применения информационного подхода к расчету планов статистического приемочного контроля изложены в работе [4]. Они базируются на фундаментальном труде С. Кульбака [3].
В предисловии к книге С. Кульбака академик А. Колмогоров писал: «аналитический аппарат теории информации был создан тогда, когда здание математической статистики было в своих основных, находящих наиболее широкое применение частях уже построено и кодифицировано. Но навыки мысли и аналитический аппарат теории информации должны, по-видимому, привести к заметной перестройке этого здания» [3, с. 5–6].
В последние годы этот подход стал применяться в самых разнообразных отраслях. Примером этому могут служить работы А.Д. Урсула [5], О.В. Цветкова [6], Е.Г. Адрианова и др. [7], Роберта Грэя [8] и других.
Как можно заметить из работ Д.В. Гаскарова, В.И. Шаповалова [2], Н.П. Кривенко [9] и других, достоверные результаты при анализе малых выборок не могут быть получены стандартными подходами математической статистики. Во всех случаях необходимо наличие некоторой априорной информации, что приводит к необходимости использования байесовского подхода.
Можно показать [4], что информационно-статистический подход при расчете планов СПК обеспечивает большую надежность и точность оценки уровня дефектности партии.
Вышеизложенное дает основания полагать, что интеграция информационного и байесовского подходов позволит адекватно оценивать качества малых партий.
В работе [4] рассмотрен информационный подход к построению планов статистического приемочного контроля. Он использует следующие понятия:
q – вероятность получения бракованного изделия;
p = 1 – q – вероятность изготовления годной детали.
Энтропия такого процесса равна
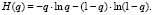 (1)
(1)
Основная характеристика плана СПК может быть вычислена по следующей формуле:
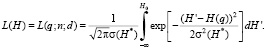 (2)
(2)
При помощи оперативной характеристики можно определить риск поставщика a и риск потребителя β.
Риск поставщика определяется как вероятность забраковать партию, в то время как входной уровень дефектности равен приемочному уровню qп. Отсюда a = 1 – L(qп). Риск потребителя β определяется как вероятность принятия партии с уровнем дефектности равным браковочному уровню qб: β = L(qб).
Как показано в работе [4], приемочное и браковочное числа можно связать с объемом выборки n следующими уравнениями:
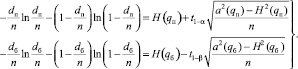 (3)
(3)
Здесь tg – g-квантиль нормального распределения.
Концепция «интегрального риска»
Суть концепции «интегрального риска» заключается, в отличие от традиционного подхода точечных оценок, в том, что рассматривается вероятность принятия или забракования партии для интервалов уровней дефектности: вероятность забраковать партию с дефектностью меньше, чем qп (интегральный риск поставщика a), и вероятность принять партию с дефектностью большей, чем qб:(интегральный риск потребителя).
Пусть известна априорная функция плотности вероятностей доли дефектных изделий в партии w(q), предъявляемой к испытаниям. Тогда можно записать следующие уравнения [1, 4]:
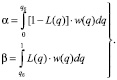 (4)
(4)
Опытным путем функция плотности вероятностей получается путем дискретизации области изменения величины q на интервалы, как правило, постоянной ширины Dq и определения частот попадания в каждый интервал.
Разобьем множество возможных значений величины q на k равных интервалов точками {0; 1/k; 2/k; …; (k – 1)/k; 1}. Пусть в каждом интервале наблюдается ni попаданий значений 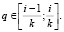
Тогда можно записать
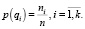 (5)
(5)
С другой стороны,
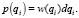 (6)
(6)
Тогда можно записать
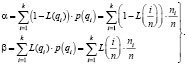 (7)
(7)
Методика расчета информационных планов СПК на основе концепции «интегрального риска»
Пусть в результате 100 наблюдений за дефектностью партий изделий получены следующие результаты (табл. 1).
Таблица 1
Эмпирическое распределение доли дефектных изделий
|
i |
qi |
Количество ni |
Доля pi = ni/n |
|
1 |
0,005 |
1 |
0,01 |
|
2 |
0,01 |
1 |
0,01 |
|
3 |
0,015 |
3 |
0,03 |
|
4 |
0,02 |
10 |
0,1 |
|
5 |
0,025 |
40 |
0,4 |
|
6 |
0,03 |
10 |
0,1 |
|
7 |
0,035 |
9 |
0,09 |
|
8 |
0,04 |
8 |
0,08 |
|
9 |
0,045 |
7 |
0,07 |
|
10 |
0,05 |
6 |
0,06 |
|
11 |
0,055 |
5 |
0,05 |
|
12 |
0,06 |
0 |
0 |
|
ИТОГО: |
100 |
1 |
|
Разместим исходные данные в таблицу Excel (рис. 1).
В табл. 2 представлена расшифровка значений ячеек.
На рис. 2 представлена копия экрана с вычисленными значениями оперативной кривой информационного плана СПК
На рис. 3 приведены результаты расчетов интегральных рисков.
Результаты исследования и их обсуждение
Анализ результатов расчета интегральных рисков (рис. 3) приводит к следующим выводам.
Если задать α = 0,05, то можно отметить, что ближайшее значение α = 0,06 (ячейка О6). Шестая строка соответствует значению q = 0,025. Это говорит о том, что вероятность забраковать партию с дефектностью q ≤ 0,025 равна 0,06.
При β = 0,05 ближайшее расчетное значение равно β = 0,035 (ячейка Q12). Двенадцатая строка соответствует значению q = 0,055. Это говорит о том, что вероятность принять партию с дефектностью q ≥ 0,055 равна 0,035.
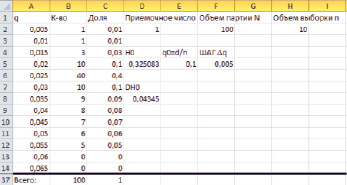
Рис. 1. Таблица исходных данных
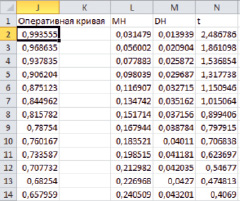
Рис. 2. Расчет оперативной кривой информационного плана СПК
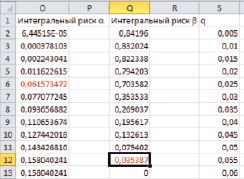
Рис. 3. Результаты расчета интегральных рисков
Таблица 2
Описание таблицы исходных данных
|
№ п/п |
Обозначение |
Адреса |
|
1 |
q – изменяемая величина границ интервалов дискретизации |
А1 … А36 |
|
2 |
К-во (ni) – количество опытов с данными значениями q |
B1 … В36 |
|
3 |
Доля (pi) – оценка вероятности наблюдения значения qi; pi = ni/n |
C1 … C36 |
|
4 |
Приемочное число (dп) |
D2 |
|
5 |
Объем партии N |
F2 |
|
6 |
Объем выборки n |
H2 |
|
7 |
q0 = dп/n – эталонное значение |
Е5 |
|
8 |
ШАГ Dq – ширина интервала дискретизации |
F5 |
|
9 |
|
D5 |
|
10 |
|
D8 |
Если учесть объем партии N = 100, то можно сделать вывод, что с вероятностью 0,06 в партии находится не более Nq = 2,5 не годных изделий в среднем; с вероятностью 0,035 в партии находится не менее 3,5 не годных изделий в среднем.
Можно исходить не из заданных интегральных рисков, а из заданных уровней qп и qб, определяя интегральные риски.
При необходимости можно менять все три основных параметра: объем партии N, объем выборки n, приемочное число d. Варьируя эти три параметра, можно получить оптимальный для текущих условий план контроля.
Выводы
Проведенные исследования дают основание утверждать, что описанный выше подход, основанный на интеграции байесовского подхода и информационно-статистического, позволяет получить адекватный результат при малых объемах выборки.




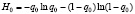 – используемый в (1,28) предел интегрирования при расчете информационного плана контроля
– используемый в (1,28) предел интегрирования при расчете информационного плана контроля