Современные низкоорбитальные системы спутниковой связи (НССС) достаточно успешно применяются для организации связи с объектами, расположенными за полярным кругом. Поэтому они используются в автоматизированных системах дистанционного контроля и управления. При этом количество таких группировок будет постоянно возрастать. В результате в зоне видимости приемника, расположенного на объекте управления добычи и транспортировки углеводородов, может появиться спутник-нарушитель, который попытается навязать ложную команду управления. Чтобы предотвратить такое навязывание и повысить информационную скрытность НССС в работе [1], предлагается использовать систему аутентификации космического аппарата (КА). Повысить скорость определения статуса КА возможно за счет использования протокола аутентификации, реализованного в модулярных кодах (МК), так как в данных кодах обеспечивается максимальная скорость выполнения модульных операций [2]. Однако после проведенных в МК вычислений необходимо выполнить преобразование к коду позиционной системы счисления (ПСС). Поэтому разработка математической и структурной моделей кодопреобразования МК-ПСС для системы аутентификации космического аппарата, характеризующихся минимальными временными затратами, является актуальной задачей.
Чтобы обеспечить высокую информационную скрытность НССС, в [1] показана система опознавания с криптостойким протоколом аутентификации. Так как данный протокол построен на доказательстве с нулевым разглашением знаний, то в нем применяются большие простые числа, что характеризуется значительными временными и схемными затратами. Реализация такого протокола в МК позволит снизить временные затраты на аутентификацию КА, так, модульные операции выполняются над малоразрядными остатками и параллельно. Однако после выполнения соответствующих вычислений необходимо результат представить в ПСС. Для этого выполняется обратное преобразование. Так как скорость выполнения данной процедуры будет зависеть от алгоритма и его схемной реализации, то целью исследований является разработка математической и структурной моделей кодопреобразования моделей для систем аутентификации космического аппарата, обладающих минимальными временными затратами.
Материалы и методы исследования
Так как большинство протоколов аутентификации на основе доказательства с нулевым разглашением знаний реализуются по большому модулю, то для сокращения времени выполнения вычислений можно использовать МК. В непозиционных модулярных кодах используются взаимнопростые основания р1, р2, ..., рk, где НОД(рi, pj) = 1 при i ≠ j, с помощью которых получают остатки целого числа А. Тогда МК представляется как
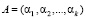, (1)
где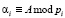
; i = 1,…, k.
Так как остатки МК значительно меньше исходного числа А, то модульные операции над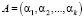 
и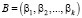 
будут выполняться быстрее, так как справедливо
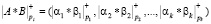, (2)
где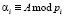 
; 
.
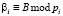Произведение оснований МК определяет его рабочий диапазон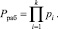 
Рассмотрим модификацию протокола аутентификации спутника, реализованной МК. В качестве секретных параметров применяются сеансовый ключ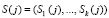 
и параметр 
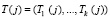, используемый для проверки нарушений использования сеансового ключа, где 
; 
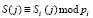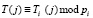. Протокол включает этапы:
1. На борту спутника сначала вычисляют истинный статус КА с помощью МК
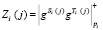, (3)
где g – первообразный элемент мультипликативной группы по модулю рi; i = 1, 2,…, k.
2. На борту КА производится «зашумление» секретных параметров
; 
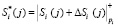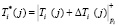. (4)
где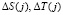
– параметры зашумления; 
; 
.
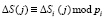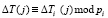3. Затем на спутнике вычисляют зашумленный статус КА, представленного в МК
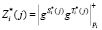. (5)
4. Для аутентификации спутника запросчик передает «вопрос» d = (d1,…, dk).
5. Ответчик, получив d = (d1,…, dk), осуществляет вычисление ответов на него
;
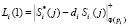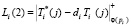. (6)
6. Ответчик выполняет обратное преобразование МК-ПСС истинного и зашумленного статусов, а также двух ответов на «вопрос» d, а затем передает их запросчику.
7. Получив ответ, запросчик осуществляет аутентификацию спутника, согласно
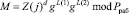, (7)
где
;
;
.
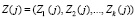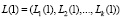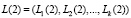Если M = Z*(j), где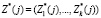 
, то спутник является «своим».
Так как модулярные коды относятся к непозиционным кодам, то обязательной немодульной операцией выступает обратное преобразование МК-ПСС. Для преобразования МК в позиционный код используют китайскую теорему об остатках (КТО) [3, 4]. Тогда
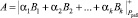, (8)
где Bi – ортогональные базисы модулярного кода СОК; rА – ранг числа А; i = 1, 2,…, k.
Так как значения ортогональных базисов могут быть просчитаны заранее и занесены в LUT-таблицы, то обратное преобразование МК-ПСС можно реализовать на основе LUT-таблиц, что позволит сократить временные затраты на перевод.
Однако в процессе обратного преобразования на основе КТО может возникнуть ситуация, когда результат суммирования будет больше, чем рабочий диапазон Рраб. Но число А, представленное в МК, не может выходить за пределы Рраб. Для этого необходимо из суммы вычесть значение рабочего диапазона до выполнения условия А < Рраб. Для этого используется позиционная характеристика ранг rА числа А. Тогда (9) можно представить
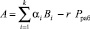. (9)
Для вычисления rА можно провести операцию целочисленного деления числа А на Рраб. Данная операция должна проводиться после получения результата суммирования. В работе [5] представлены алгоритмы деления с восстановлением и без восстановления остатков. Так, при использовании алгоритма деления с восстановлением остатка время вычисления одного разряда частного определяется как
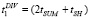, (10)
где tSUM – время выполнения суммирования; tSUM – время выполнения операции сдвига.
Снизить временные затраты возможно за счет использования алгоритма деления без восстановления остатка, для которого время вычисления одного разряда частного равно
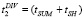. (11)
При использовании операции деления при вычислении ранга rА временные затраты на выполнение обратного преобразования МК-ПСС будут определяться
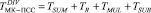, (12)
где TSUM – время суммирования произведений остатков МК на ортогональные базисы; TR – время вычисления ранга числа; TMUL – время умножения ранга числа на Рраб; TSUB – время выполнения операции вычитания.
Сократить временные затраты можно за счет использования модифицированного алгоритма вычисления ранга в МК. Так как значение rА зависит от количества оснований МК, то его вычисления вводят дополнительное основание pg, удовлетворяющее
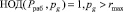, (13)
где rmax – максимальное возможное значение ранга при переводе МК-ПСС.
Введение нового основания pg делает справедливым следующее выражение
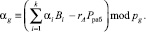(14)
Тогда получаем
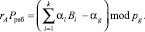(15)
Разделим обе части выражения (15) на рабочий диапазон. Тогда получаем
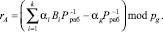(16)
Воспользуемся свойствам ортогональных базисов. Тогда имеем
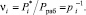(17)
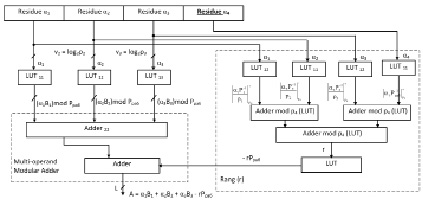
Структурная модель обратного преобразователя МК-ПСС
Подставим (17) в выражение (16). Положив, что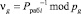 
, получаем
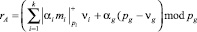. (18)
Вычисленное значение ранга числа rA умножается на величину (- Рраб). Для этого можно использовать LUT-таблицу. Полученный результат подается на сумматор, где он суммируется с результатом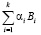 
. В результате получается позиционный код числа А. На основании разработанной математической модели преобразования МК-ПСС была создана структурная модель кодопреобразователя, которая показана на рисунке.
Результаты исследования и их обсуждение
Рассмотрим применение разработанных математической и структурной моделей преобразователя МК-ПСС. Для системы аутентификации КА взяты р1 = 11, р2 = 13 и р3 = 19.
Вычислим значение ортогонального базиса для первого основания кода СОК р1 = 11. Тогда на основе алгоритма [3] имеем:
1. Вычислим значение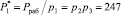 
.
2. Вычислим остаток полученного произведения 
.
3. Значение веса ортогонального базиса m1 = 9, так как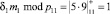 
.
4. Значение ортогонального базиса равно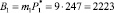 
.
Аналогичным образом получаем ортогональные базисы В2 = 209 и В3 = 286.
Пусть число А = 477 = (4, 9, 2). Так как rmax = 2, то для вычисления ранг выбираем основание р4 = 7. Тогда МК числа А = 477 = (4, 9, 2, 1). Остатки числа записываются в регистры преобразователя. Затем остатки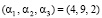 
поступают на входы таблиц LUT11 – LUT13, с выхода которых снимаются значения сумму парных произведений
; 
;
.
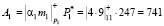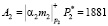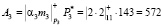Результат подается на входы сумматора Adder22, с выхода которого снимается
A* = А1 + А2 + А3 = 3194.
Параллельно с данными вычислениями происходит определение величины ранга числа. Остатки числа подаются на входы таблиц LUT11 – LUT14 блока вычисления ранга. Данные ПЗУ осуществляют операцию умножения остатков кода СОК на константы vi,
; 
; 
; 
.
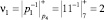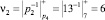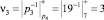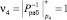Результаты умножения остатков на данные константы поступают на сумматор. Тогда
.
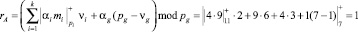Значение rA = 1 подается на вход таблицы LUT, где умножается на величину (- Рраб). Результат подается на сумматор Adder, где суммируется с результатом А*. Тогда имеем
.
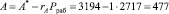Осуществим перевод МК-ПСС, используя китайскую теорему об остатках
.
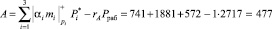Временные затраты на обратное преобразование МК-ПСС при использовании разработанной математической и структурной моделей составят
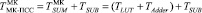. (19)
Время считывания данных из LUT-таблицы будет определяться τэ – временем срабатывания логических схем совпадения, т.е. TLUT = τэ. При использовании алгоритма суммирования CAS для нахождения суммы двух операндов достаточно двух тактов работы одноразрядного сумматора tSUM. Так как в сумматоре Adder складывается k парных произведений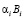 
, то справедливо
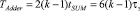. (20)
Так как операция выполняется на позиционном сумматоре, то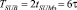 
. Тогда
.
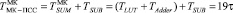Определим временные затраты на преобразование МК-ПСС с использованием алгоритма деления с восстановлением остатка. Так как rmax = 2, то время вычисления ранга
,
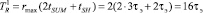где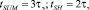 
.
При использовании алгоритма деления без восстановления остатка получаем
.
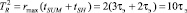Тогда время обратного преобразования МК-ПСС будет равно
.
.
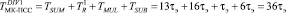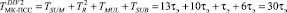Сравнительный анализ показывает, что разработанная математическая модель преобразования МК-ПСС на основе КТО позволяет в 1,94 раза быстрее выполнить обратное преобразование в позиционный код по сравнению с алгоритмом деления с восстановлением остатка, и в 1,54 раза – с без восстановления остатка. Очевидно, что разработанные математическая и структурная модели кодопреобразователя МК-ПСС целесообразно применять в системе аутентификации КА, функционирующей в модулярных кодах, так обеспечивают минимальные временные затраты.
Заключение
Для обеспечения минимальных временных затрат на аутентификацию КА целесообразно использовать МК. Однако для перехода от непозиционного МК к коду ПСС необходимо выполнить обратное преобразование. Поэтому разработка математической и структурной моделей преобразования МК-ПСС, обладающих минимальными временными затратами, является актуальной задачей. В статье представлены математическая и структурная модель преобразования МК-ПСС на основе КТО, применение которых позволяет в 1,94 раза быстрее выполнить обратное преобразование в позиционный код по сравнению с алгоритмом деления с восстановлением остатка и в 1,54 раза – с без восстановления остатка. Очевидно, что разработанные математическая и структурная модели кодопреобразователя МК-ПСС целесообразно применять в системе аутентификации КА, функционирующей в МК, так обеспечивают минимальные временные затраты.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-07-01020.