В промышленности уже заняло достаточно прочные позиции плазменное напыление покрытий. При этом зачастую эффективному использованию плазменных технологий препятствует недостаток систематизированной информации о закономерностях и возможностях соответствующих технологических процессов, что затрудняет выбор оптимальной технологии для решения конкретных производственных задач, назначение режимов обработки, прогнозирование результатов [1].
До настоящего времени источником основной информации о процессе образования плазменной струи с необходимыми эксплуатационными характеристиками остается эксперимент. Поэтому большое значение при планировании плазменного напыления приобретает экспериментальное построение формальной модели при широком применении математических методов планирования.
При этом стоит учитывать, что при описании физических и химических характеристик плазменного напыления, в частности преобразования композитного порошкового вещества под действием приложенного к нему импульса давления, применение математического моделирования – весьма трудоемкий и сложный процесс. Поэтому разрабатываются математические модели, которые учитывают конкретные преобразования композитного вещества в ходе его эксплуатации [2].
Цель исследования: разработка математической модели на основе распространения нестационарных волн в трехкомпонентной среде при образовании плазменной струи.
Материалы и методы исследования
Вопросу по распространению упругих волн в двухкомпонентных средах посвящено множество научных трактатов и работ. Среди них стоит выделить труды заслуженного ученого М.А. Био [3–5].
Взаимосвязывающее перемещение твердого тела (композитного порошка), газа и жидкости будем рассматривать как перемещение порошка, жидкости и газа в деформируемой пористой среде.
Введем уточнение, что габаритные размеры пор весьма малы в сравнении с расстоянием, на котором значительное изменение претерпевают кинематические и динамические показатели движения. Что в итоге позволяет нам полагать, что три среды сплошные и в любой координате пространства будет три вектора смещения [6].
Доказано, что в такой среде в общем случае распространяется три волны, скорости которых существенным образом зависят от направления распространения волновой поверхности.
Стоит отметить, что материалы (композитный порошок, плазмообразующие газы и плазма) весьма неоднотипно реагируют на приходящиеся на них нагрузки и факторы внешней среды. Следовательно, для каждой среды должны быть заданы реологические соотношения, отражающие ее термомеханические свойства. Отталкиваясь от заданной температуры и давления при плазменном напылении, одно и то же вещество может находиться в твердом, жидком или газообразном состоянии, а его реологическая модель будет либо упругой, либо вязкой и т.д. Чтобы решить приведенную особенность плазменного напыления, для описания эксплуатационных параметров веществ, применяемых на всех стадиях процесса, вводится понятие – идеализированная среда [7].
На базе идеализированной среды запишем систему уравнений, определяющую динамическое поведение упругой, насыщенной жидкостью и газом трехкомпонентной среды в перемещениях компонент [6], выражая коэффициенты Ламе λ, μ через модуль Юнга E и коэффициент Пуассона v по формулам [8]:
, 
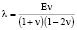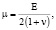
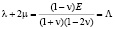(1)
– полный тензор напряжений в скелете при наличии жидкости и газа в порах:
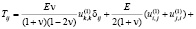
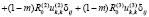(2)
– силы, действующие на плазму (жидкость) и плазмообразующий газ:
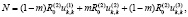(3)
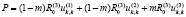
– уравнения движения пористой среды:
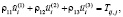
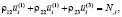(4)
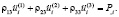
Здесь ρ11, ρ22, ρ33 – эффективные плотности порошковой механической смеси для плазменного напыления, плазмы и плазмообразующего газа соответственно (кг/м3); ρ12 < 0, ρ13 < 0, ρ23 < 0 – коэффициенты динамической связи скелета; R0(2), R0(3) – коэффициенты сжимаемости компонент, заполненных жидкостью и газом; uj(α) – перемещения компонент. В скобках цифры вверху обозначают: 1 – твердая компонента, 2 – жидкость, 3 – газ. Предполагается ρji, = ρij. По повторяющимся индексам здесь и в дальнейшем проводится суммирование от 1 до 3.
Под волной ускорения в наполненной композитными элементами плазмой и плазмообразующим газом трехкомпонентной пористой среде понимается поверхность, на которой напряжения и силы, направленные на плазменный поток, плазмообразующий газ, композитные элементы и скорости перемещения компонент непрерывны.
Продифференцируем соотношения (2) и (3) по t и получим
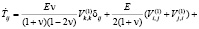
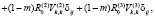
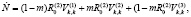(5)
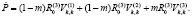
Запишем уравнениям (4) и соотношения (5) разрывов [9]:
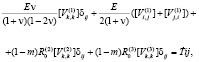
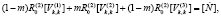
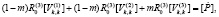(6)
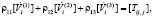
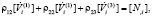
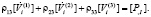
К соотношениям (6) применим кинематические и геометрические условия совместности первого порядка на поверхности разрыва [10]:
, 
, 
, 
, 
, 
, 
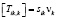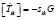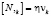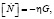
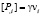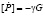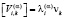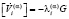
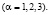(7)
Здесь sik,η, γ, λi(1), λi(2), λi(3) – величины, характеризующие скачки первых производных напряжений, сил, действующих на плазму и плазмообразующий газ и скоростей перемещения компонент; vi – единичный вектор нормали к волновой поверхности; G – скорость распространения волновой поверхности пористой среды.
Используя условия (7), формулы (6) запишем в виде
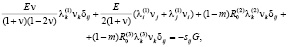
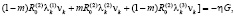
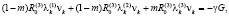(8)
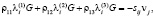
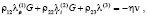
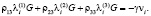
Исключая из (8) величины sij, η, γ, получим однородную систему уравнений относительно λk(1), λk(2), λk(3) [11]:
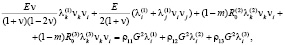
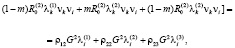(9)
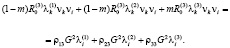
Полагая, что λk(α)vk ≠ 0, на волновой поверхности, умножим (9) на vi и просуммируем по повторяющемуся индексу i, получим однородную систему трех линейных уравнений относительно wα = λk(α)vk (α = 1, 2, 3):
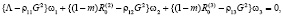
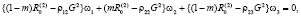(10)
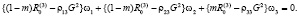
Введем следующие обозначения:
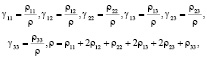(11)
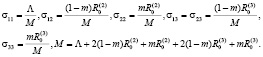
С учетом (11) систему (10) запишем в безразмерной форме:
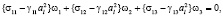
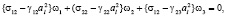(12)
, 
, 
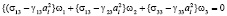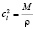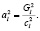
Условие существования нетривиальных решений системы (12), однородной относительно w1, w2, w3 определяет три скорости волн ускорений в насыщенной жидкостью и газом пористой среде, которые находятся из определителя третьего порядка, составленного из коэффициентов при неизвестных w1, w2, w3 системы (12):
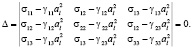(13)
Для вычисления определителя Δ справедлива формула разложения данного определителя по элементам i-го столбца [12]:
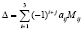
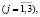(14)
где i – номер столбца; j – номер строки; aij – элемент определителя, стоящий на пересечении i-й строки и j-го столбца; Mij – минор элемента матрицы третьего порядка.
Раскрывая определитель (13) по формуле (14) и сделав замену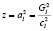 
, получим кубическое уравнение относительно z:
,
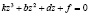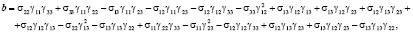
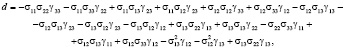(15)
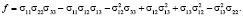
Коэффициенты σ11… σ33 находятся по формулам (11). Решение кубического уравнения (15) находим по формулам Кардана [13]. Для решения уравнения (15) разделим его на k и введем новую переменную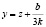 
, тогда после преобразования получим:
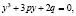
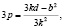
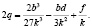(16)
Вычислим дискриминант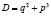 
. Если D < 0, то рассматриваемое уравнение обладает тремя действительными корнями, которые записываются как комплексные величины. Если D > 0, то уравнение имеет несколько различных решений, а именно одно действительное и два мнимых. Если D = 0, то имеем три совпавших нулевых корня или имеем три действительных решения, два из которых совпадают.
Таким образом, в трехкомпонентной пористой среде распространяются три продольные волны в зависимости от дискриминанта кубического уравнения. Если связь между компонентами жидкость – газ и упругость – газ в среде отсутствует γ13 = 0, γ23 = 0, σ23 = 0, то кубическое уравнение (15) сводится к квадратному уравнению:
, 
, 
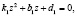
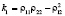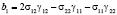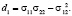(17)
Уравнение (17) совпадает с уравнением работы [6].
Положим в системе (9) λi(α)vi (α = 1, 2, 3).Тогда получим G = Gt:
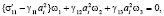
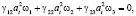
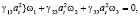(18)
, 
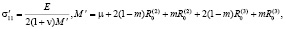
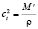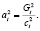
Условием существования ненулевых решений системы (18) является ее определитель, составленный из коэффициентов при λi(α) (α = 1,2,3) и который должен быть равен нулю:
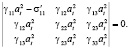(19)
Раскрывая уравнение (19) по формуле (14), получим выражение для нахождения скорости поперечной волны, распространяющейся в трехкомпонентной среде:
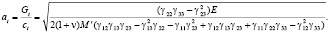(20)
Если связь между плазмой и плазмообразующим газом, композитным материалом и плазмообразующим газом отсутствует, γ23 = 0, γ13 = 0, то из (20) следует
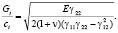(21)
Формула (21) совпадает с формулой, полученной в работе [6].
Результаты исследования и их обсуждение
Согласно внесенным данным в идеализированную среду, а также результатам расчетов уравнений (11), получаем сводную таблицу значений.
Таблица значений тензоров напряжений и весовых коэффициентов
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
|
σ11 |
1 |
1 |
1 |
1 |
1 |
|
σ12 |
6,5E-13 |
6,14E-13 |
5,86E-13 |
5,63E-13 |
5,46E-13 |
|
σ22 |
1,15E-13 |
1E-13 |
8,75E-14 |
7,68E-14 |
6,75E-14 |
|
σ13 |
1,08E-12 |
1,06E-12 |
1,05E-12 |
1,01E-12 |
9,71E-13 |
|
σ23 |
1,08E-12 |
1,06E-12 |
1,05E-12 |
1,01E-12 |
9,71E-13 |
|
σ33 |
1,91E-13 |
1,73E-13 |
1,58E-13 |
1,37E-13 |
1,2E-13 |
|
γ34 |
1,049211 |
1,044258 |
1,039306 |
1,094341 |
1,061377 |
|
γ12 |
–0,01 |
–0,015 |
–0,02 |
–0,015 |
–0,012 |
|
γ22 |
0,020493 |
0,01647 |
0,030446 |
0,030423 |
0,017399 |
|
γ13 |
–0,04 |
–0,03 |
–0,02 |
–0,08 |
–0,05 |
|
γ23 |
–0,01 |
–0,001 |
–0,01 |
–0,015 |
–0,005 |
|
γ33 |
0,050296 |
0,031272 |
0,030248 |
0,095236 |
0,055224 |
На основе таблицы сводных значений тензоров напряжений и весовых коэффициентов составим графики зависимостей. На рис. 1 и 2 изображена зависимость скорости распространения продольной упругой волны в композитном материале от его физико-механических характеристик – модуля Юнга и коэффициента Пуассона.
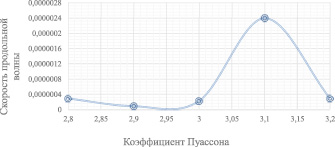
Рис. 1. Зависимость коэффициента Пуассона от скорости распространения продольной волны
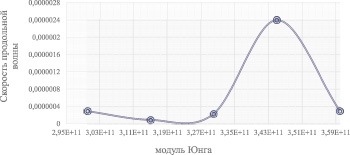
Рис. 2. Зависимость модуля Юнга от скорости распространения продольной волны
Выводы
Разработана математическая модель на основе распространения нестационарных волн в трехкомпонентной среде при образовании плазменной струи.
Построены графики зависимости скорости распространения продольных волн в материале плазменного покрытия от его технических модулей, таких как модуль Юнга и коэффициента Пуассона.