Вопросы эффективного производства тепловой энергии котельными установками принимают особое значение в условиях роста тарифов на топливо и ужесточения экологических требований. При этом эффективность работы котельных установок во многом определяется не только их техническим состоянием, но и применением интеллектуальных систем управления производством, использующих развитые методы и алгоритмы анализа данных [1]. В данной работе предлагается математическая модель, которая представляет собой необходимый шаг для построения интеллектуальных алгоритмов анализа работы котельного агрегата, причем вид модели и детальность описания объекта определяются ее целевым назначением.
Цель исследования: построение математической модели котлоагрегата и проведение имитационного моделирования, демонстрирующего ее возможности для анализа тепловых процессов.
Материалы и методы исследования
В качестве фундаментальных уравнений при построении данной модели принимаются уравнения теплового баланса для топочной камеры, барабана котла и пароперегревателя.
Тепловой баланс в камере сгорания котла описывается выражением
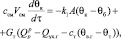(1)
где ссм – средняя объемная теплоемкость газовоздушной смеси в камере сгорания, Дж/(м3·К); ст – объемная теплоемкость топлива, Дж/(м3·К); Vсм – объем газовоздушной смеси, м3; k1 – коэффициент теплопередачи от дымовых газов, Вт/(м2·К); F – площадь поверхности теплопередачи, м2; θk – температура в камере сгорания, К; θб – температура в барабане котла, К; θв.г. – температура воспламенения топлива, К; θт – температура подаваемого в камеру сгорания топлива, К; Gт – объемный расход топлива в камере сгорания, м3/с;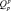 
– высшая теплота сгорания топлива, Дж; Qух.г. – потери теплоты с дымовыми газами, покидающими котлоагрегат, Дж.
Уравнение теплового баланса в барабане котла:
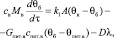(2)
где св – удельная теплоемкость воды в барабане, Дж/(кг·К); Мв – масса воды в барабане котла, кг; Gпит.в – массовый расход питательной воды в барабан, кг/с; спит.в – теплоемкость питательной воды, Дж/(кг·К); θпит.в – температура питательной воды, К; θ – удельная теплота парообразования, Дж/кг; D – массовый расход воды на парообразование (паропроизводительность), кг/с.
В адиабатных условиях выделяющееся количество теплоты идет на увеличение степени нагрева дымовых газов [2]. Теоретическую температуру горения топлива в топке θк вычисляют по формуле
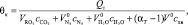(3)
где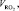 
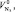
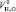– теоретические объемы продуктов сгорания топлива, м3/кг;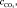 
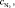
схв – средние объемные теплоемкости углекислоты, азота, водяных паров и воздуха, кДж/(м3К); αТ – коэффициент избытка воздуха в топочной камере.
Аэродинамическое несовершенство топочных устройств проявляется в том, что температура газов по мере движения по газовоздушному тракту понижается, поэтому энтальпию дымовых газов перед пароперегревателем рассчитывают по действительной температуре дымовых газов на выходе из топки:
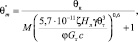(4)
где М – расчетный коэффициент, значение которого определяется относительным местоположением максимума температуры в топке; ζ – условный коэффициент загрязнения лучевоспринимающих поверхностей; γ – степень черноты топки; Hл – лучевоспринимающая поверхность нагрева, м2; φ – коэффициент сохранения теплоты; с – средняя суммарная теплоемкость продуктов сгорания 1 м3 топлива в интервале температур, кДж/(м3/К).
Энергия пара в пароперегревателе увеличивается за счет теплопередачи от дымовых газов посредством специально предназначенных для этого конструктивных элементов:
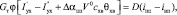(5)
где 
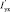и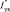 
– энтальпия продуктов сгорания перед пароперегревателем и после него, кДж/м3; Δαпп – присос воздуха в газоходе пароперегревателя; V0 – теоретически необходимый объем воздуха для сгорания 1 м3 природного газа, м3; θхв – температура воздуха в котельной, К; iнп и iнп – энтальпии перегретого пара на выходе из пароперегревателя и насыщенного пара на входе в пароперегреватель, кДж/кг.
В описание теплового баланса топочной камеры котельного агрегата входит высшая теплота сгорания топлива, которая может быть описана следующим образом на 1 м3 газового топлива:
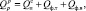(6)
где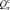 
– низшая теплота сгорания газообразного топлива, кДж; Qф.т. – физическая теплота топлива, кДж; Qф.в. – физическая теплота воздуха при его предварительном подогреве вне котельного агрегата, кДж [3].
Тепловые потери, приходящиеся на единицу объема сжигаемого топлива, связаны с недостаточным охлаждением продуктов сгорания за пароперегревателем:
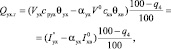(7)
где Vух – объем уходящих газов на выходе из последнего газохода котлоагрегата на 1 м3 природного газа, м3; срух – средняя объемная теплоемкость газов при постоянном давлении, определяемая по θух, кДж/(м3?/К); θух – температура уходящих газов на выходе из последнего газохода, К; θух – коэффициент избытка воздуха за котлоагрегатом; q4 – потеря теплоты от механической неполноты сгорания, %;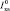 
– энтальпия холодного воздуха, кДж/кг.
Можно предположить, что поверхность теплоприемника мгновенно передает теплоту водному объему. Тогда определяющим пунктом теплообмена становится граница «стенка – вода», которая описывается через коэффициент теплоотдачи α1, и выгодно использовать модель перемешанного потока [4]. Количество теплоты, передаваемое от дымовых газов к теплоприемнику за счет излучения и конвекции, рассчитывается следующим образом:
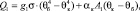(8)
где σ – постоянная Стефана – Больцмана, Вт/(м-2*К-4); αк – коэффициент теплоотдачи топочных газов конвекцией, Вт/(м2*К); A1 – поверхность теплоприемника, которая получает теплоту конвекцией, м2; g1 – общее сопротивление передачи теплоты излучением от газа к теплоприемнику, учитывающее многократное отражение от всех поверхностей, и излучение, отраженное от экранов [5]. Если отражающая и поглощающая поверхности разделены, причем последняя представляет собой плоскость, общее сопротивление излучению равно
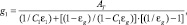(9)
где εг – средний коэффициент излучения газа; ε1 – коэффициент излучения поверхности поглотителя; C1 – доля общей поверхности, перекрываемой поверхностью поглотителя теплоты. Расчет степени черноты газов εг смеси H2O и CO2 можно провести по упрощенной методике:
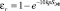, (10)
где k – коэффициент ослабления лучей в смеси, определяемый эмпирической формулой
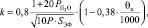(11)
где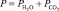 
– суммарное парциальное давление водяного пара и углекислого газа, МПа; SЭФ – эффективная длина луча, м [6].
Выражение (9) учитывает лишь часть термического сопротивления, относящуюся к границе «дымовые газы – стенка». Полное сопротивление вычисляется по формуле
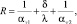(12)
где αт1 – эквивалентный коэффициент теплоотдачи от топочных газов стенке, Вт/(м2*К); αт2 – коэффициент теплоотдачи от стенки к воде, Вт/(м2*К); δ – толщина стенки, м; λ – теплопроводность стенки, Вт/м•К [7]. В результате работы теплообменника на поверхности теплопередачи образуются осаждения, которые могут заметно увеличить сопротивление теплопередаче.
На величину коэффициента αт2 влияет давление рн и плотность теплового потока q:
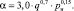(13)
Характер изменения αт2 не является монотонным и проходит через два кризиса кипения. Расчет первой и второй критических тепловых нагрузок выполняют с использованием гидродинамической модели кризисов кипения С.С. Кутателадзе.
Пароперегреватели в зависимости от ключевого способа теплопередачи подразделяют на конвективные, радиационные и полурадиационные. Вне зависимости от типа пароперегревателя при сжигании и газообразного топлива, и мазута коэффициент теплопередачи k2 определяется по формуле
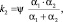(14)
где α1 – коэффициент теплоотдачи от дымовых газов к поверхности пароперегревателя, Вт/(м2*К); α2 – коэффициент теплоотдачи от стенки пароперегревателя насыщенному пару, Вт/(м2*К) [8]. При моделировании технических объектов и систем теплоэнергетики расчет ключевых величин может быть выполнен с опорой на условия подобия [9]. Коэффициент теплоотдачи от стенки к пару при продольном омывании нагретым паром рассчитывается следующим образом:
α2 = αн*Сd , (15)
где αн – коэффициент теплоотдачи, значение которого определяется по номограмме в зависимости от технологических параметров пара; Сd – поправка на диаметр, определяется по дополнительному полю вышеупомянутой номограммы в зависимости от внутреннего диаметра пароперегревателя.
Механизм теплопроводности при кипении описывается моделью пограничного слоя; с этой позиции правомерно оперировать коэффициентом теплоотдачи αкип, который позволяет судить о характере кипения, тем самым сократив риск выхода из строя тепловых элементов энергетических установок [10].
Полученная система уравнений (1–15) является моделью с сосредоточенными параметрами, которая при введении инерционности пароводяного тракта позволяет оценить реакцию системы на возмущающее воздействие по расходу топлива.
Результаты исследования и их обсуждение
Возможности модели иллюстрируются на примере модельного эксперимента, в качестве исходных данных использовались технические характеристики котлоагрегата БКЗ-210-140. Это котельный агрегат однобарабанный, вертикально-водотрубный, с естественной циркуляцией П-образной компоновки (табл. 1).
Таблица 1
Характеристики БКЗ-210-140
|
Наименование |
Величина |
|
Паропроизводительность, т/ч |
210 |
|
Температура перегретого пара, °С |
545 |
|
Температура питательной воды, °С |
230 |
|
Лучевоспринимающая поверхность нагрева экранов топки, м2 |
716 |
|
Поверхность нагрева пароперегревателя, м2 |
2561 |
|
Давление в барабане котлоагрегата, кгс/см2 |
155 |
|
Водяной объем котла, м3 |
58,5 |
|
Паровой объем котла, м3 |
30,7 |
|
Объем топочной камеры, м3 |
1093 |
Для получения динамических характеристик объекта используется возмущающее воздействие по расходу топлива, которым является природный газ. Состав топлива приведен в табл. 2.
Таблица 2
Состав топлива
|
СН4 |
С2Н2 |
С2H4 |
С2Н6 |
С3Н8 |
С4Н10 |
С5Н12 |
N2 |
СО2 |
H2 |
|
|
% |
97,84 |
0 |
0 |
0,1 |
0,03 |
0,02 |
0,01 |
1,7 |
0,3 |
0 |
На пятой секунде наносится возмущающее воздействие по расходу топлива Gт, который на седьмой секунде превышает начальное значение на 10 %. С помощью уравнений (1–15) получены графики изменения температуры в топочной камере θk, температуры перегретого пара θпп и коэффициента полезного действия котельного агрегата η (рисунок).
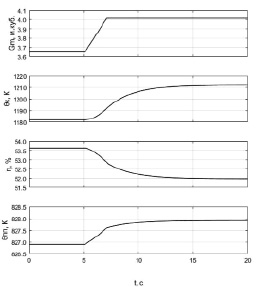
Результаты модельного эксперимента
Результаты имитационного моделирования иллюстрируют, что процессы в топочной камере протекают с достаточно высокой скоростью, что согласуется с кинетикой горения при перемешанном потоке.
Заключение
Возможности модели не ограничиваются результатами приведенного эксперимента. Построенная модель котлоагрегата позволяет оценивать в то же время инерционность барабана котла, которая обусловливает большую задержку в динамике нагрузки, что важно для прогнозирования аварийных режимов, вытекающих из выхода технологческих параметров на новые установившиеся значения. Таким образом, учет в модели разнотемповости тепловых процессов в котельном агрегате является основанием для предотвращения возможных аварийных ситуаций (например, пережога экранных труб).
Модель обладает и другими полезными свойствами: предполагая безотказную работу системы управления технологическим процессом, она оставляет тем не менее пространство для испытания различных алгоритмов управления и устройств, отрабатывающих простейшие законы регулирования или их комбинацию.
Дальнейшее развитие работы авторам видится в направлении доработки модели, позволяющей рассматривать работу котлоагрегата под нагрузкой, например, в составе энергоблока. Это расширит возможности анализа, повысив в то же время практическую ценность исследования.