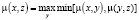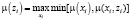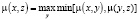В настоящее время особо актуален комплекс задач математического моделирования изучаемых геологических объектов нефтегазовой геологии. В частности, построение трехмерных геологических моделей месторождения. Основной информацией для построения качественной трехмерной модели являются достоверные и качественные результаты интерпретации ГИС-параметров.
Традиционно для построения петрофизической модели применяются методы статистической обработки информации [1] и выполняется замена экспериментального материала рассчитанными законами и определенной интегральной, единой для всей зависимости, оценкой меры тесноты зависимости. В соответствии с установленным методом, далее полученный закон в форме уравнений зависимости между параметрами переносится на исследуемый объект. При этом важно знать: какова неопределенность конечного прогноза, включающая всю цепочку участвующих в прогнозе преобразований. Данная информация является необходимой для снижения технико-экономических рисков, связанных с формированием проекта разработки месторождения. Необходимо пересчитывать неопределенности в данных и зависимостях в итоговую неопределенность прогнозных параметров. Статистические методы построения петрофизических моделей не дают такой возможности, поэтому данный путь нередко считается основой ошибочных геологических заключений о ресурсах и запасах углеводородного сырья регионов [2, 3].
Выходом в данной ситуации является построение нечетких петрофизических моделей, которые позволяют отражать нечеткость исходных данных, и использование методов нечеткого прогнозирования.
Метод нечеткого прогнозирования параметров геологической модели является альтернативой методики построения прогноза определяемых по ГИС параметров, основанной на использовании корреляционных связей. Обобщенная технологическая схема нечеткого прогнозирования основана на нечетких петрофизических моделях и теоретических принципах нечеткого логического вывода, выраженного в построении композиций Мамдани и нечётких композиций в целом.
В таблице приводится соответствие между действиями в методах на основе традиционного регрессионного анализа и их условных аналогов в технологии нечеткого прогнозирования.
Технологическая таблица соответствий
|
Традиционная регрессионная схема |
Метод нечеткого прогнозирования |
Примечание |
|
Уравнение регрессии y = f(x) |
Функция принадлежности μ(x, y) |
Поле достоверности данных используется вместо выборки вдоль линии регрессии |
|
Подстановка в уравнение z = φ(y) уравнения y = f(x):z = φ(f(x)) |
Композиция
|
Нечеткая петрофизическая модель отражает реальные данные, используется вместо идеализированной зависимости между переменными |
|
Прогноз по значениям xi величин zi = φ(f(xi)) |
Прогноз функции принадлежности
|
Вместо прогнозного значения выбранного из zi = φ(f(xi)) вводится нечеткая модель реальных измерений φ(xi) и прогнозируется поле достоверности итогового параметра zi |
|
Замена переменных в уравнении петрофизической модели y = f(x) на новую переменную z = φ(y) (расчет z по y) |
μ(x, z) = μ(y, x)*G[z, φ(y)] |
G[z, φ(y)] – надграфик для z = φ(y), представляюший собой на плоскости переменных X, Y множество точек {z, φ(y)}. Частный случай композиции
|
Цель исследования: демонстрация таких компонент технологии нечеткого прогнозирования, как построение нечетких петрофизических моделей нефтепромысловых параметров в условиях неопределенности и построение композиций.
Материалы и методы исследования
Исходные геолого-геофизические данные для построения нечетких петрофизических композиций были получены по скважинам Тимано-Печорской нефтегазоносной провинции, к ним относятся одновременно измеренные значения параметров пористости и проницаемости (рис. 1, а), проницаемости и остаточной водонасыщенности (рис. 1, б).
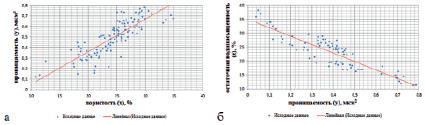
Рис. 1. Исходные данные: а) Отношение «Пористость – Проницаемость»; б) Отношение «Проницаемость – Остаточная водонасыщенность»
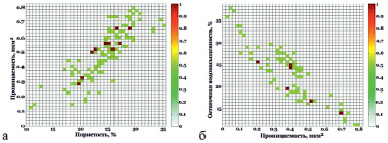
Рис. 2. Карта плотности данных: а) Отношение «Пористость – Проницаемость»; б) Отношение «Проницаемость – Остаточная водонасыщенность». Цветовая палитра отображает, сколько данных находится в каждой ячейке сетки
Первым этапом является представление исходных данных s = {s1, s2, s3…si; i = 1…N} в форме нечетких отношений – построении нечеткой петрофизической модели, основанное на конструировании функции принадлежности.
Для отношения «Пористость – Проницаемость» исходные данные s = {Кп, Кпр}. Для отношения «Проницаемость – Остаточная водонасыщенность» исходные данные s = {Кпр, Ков}.
Исходные данные покрываются сеткой и рассчитывается: сколько данных попало в каждую ячейку сетки (рис. 2), затем задается уровень погрешности и по невязке определяется необходимое количество источников данных:
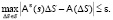
Функция принадлежности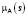 
рассчитывается как нормированное к единице поле рассеяния 
:
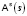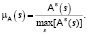
Поле рассеяния имеет смысл диффузионного рассеяния в бесконечном однородном пространстве параметров точечных источников и рассчитывается по формуле
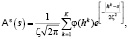
где hk – координаты расположения источников, φ(hk) – значения источников, ζ – значение эффективного параметра рассеяния [4]. Эффективный параметр отвечает за размытие функций принадлежности.
Результаты представления исходных данных в форме нечетких отношений для петрофизических зависимостей «пористость – проницаемость» и «проницаемость – остаточная водонасыщенность» представлены на рис. 3.
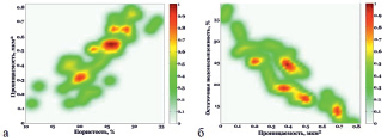
Рис. 3. Нечеткие отношения: а) «Пористость – Проницаемость»; б) «Проницаемость – Остаточная водонасыщенность». Здесь и далее цветовая палитра отображает уровень достоверности
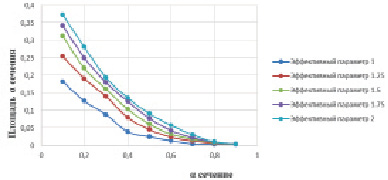
Рис. 4. Графики зависимости относительной меры от параметра α для функций принадлежности «Пористость – Проницаемость». На легенде указано, при каких значениях эффективного параметра построены функции принадлежности
Ключевым моментом при построении функций принадлежности является подбор значения эффективного параметра. Для этого был разработан анализ α-сечений функций принадлежности. Анализ заключается в построении функций принадлежности при разных значениях эффективного параметра и графиков зависимости относительной меры (площади, занимаемой частью функции принадлежности, которая имеет достоверность выше уровня α) от параметра α. При небольших значениях эффективного параметра данная зависимость имеет характер ломаной линии, при увеличении параметра зависимость начинает плавно убывать. Оптимальным значением эффективного параметра является наименьшее значение, при котором зависимость относительной меры от параметра α плавно убывает.
На рис. 4 приведены графики зависимости относительной меры от параметра α для функций принадлежности «Пористость – Проницаемость», построенных при значениях эффективного параметра, меняющегося от 1 до 2 с шагом 0,25. Оптимальным эффективным параметром в данном случае является значение 1,5.
Коэффициент нефтенасыщенности месторождения определялся расчетным путем по формуле Кн = 1 – Ков. При этом коэффициент водонасыщенности определялся по зависимости Кв = f(Кп), полученной по данным керна. Построение взаимосвязи Кв = f(Кп) реализуется через промежуточный параметр проницаемости (Кпр).
Процедура построения нечеткой петрофизической модели для зависимости «Пористость – Проницаемость» называется композицией. Логически непротиворечиво и математически корректно сделать это можно многими способами. Вот некоторые из них: Максминная нечёткая свёртка (композиция) или правило нечеткого логического вывода Мамдани [5], Max-prod композиция, Min-max композиция, Max-max композиция, Min-min композиция, Min-average композиция. Именно композиция Мамдани, теоретически обоснованная адекватности алгебраическим операциям с матрицами, берется за основу в конструировании методов нечеткого прогнозирования.
При выборе построения композиций нечетких отношений решаются две задачи:
– во-первых, задача исключения зависимых нечетких переменных при конструировании нечеткой петрофизической модели. В нашем случае это означает нахождение нечеткой петрофизической модели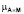 
(Кп, Кв), связи параметров (Кп, Кв) по известным нечетким отношениям 
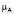(Кп, Кпр) и 
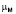(Кпр, Ков).
При этом для «четкого» случая, композиции нечетких отношений эквивалентны операциям подстановки для обычных функций.
Так, между двумя двухмерными функциями принадлежности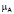 
(Кп, Кпр) и 
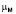(Кпр, Ков) может быть построена следующая композиция (Мамдани):
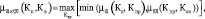
которая аналогична матричному умножению. Это правило аналогично подстановке в обычное четкое уравнение, между парой четких переменных (Кп, Кпр) уравнения, между другой парой переменных (Кпр, Ков), с целью исключить из результата переменную Кпр и получить уравнение связи между (Кп, Кв).
Композиция нечетких отношений «Пористость – Проницаемость» и «Проницаемость – Остаточная водонасыщенность», в результате которой получаем нечеткое отношение «Пористость – Остаточная водонасыщенность», представлена на рис. 5;
– во-вторых, композиции нечеткого отношения с надграфиками функций. Эта операция называется заменой переменных. В нашем случае переход от параметра водонасыщенности к параметру нефтенасыщенности с помощью линейной обратной зависимости.
Композиция нечеткого отношения «Пористость – Остаточная водонасыщенность» и надграфика функции Кн = 1 – Ков, в результате которой получаем нечеткое отношение «Пористость по керну – Нефтенасыщенность», представлена на рис. 6.
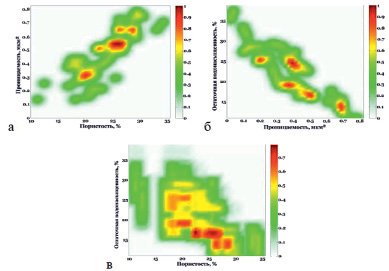
Рис. 5. Композиция нечетких отношений: а) функция принадлежности «Пористость – Проницаемость»; б) функция принадлежности «Проницаемость – Остаточная водонасыщенность»; в) функция принадлежности «Пористость – Остаточная водонасыщенность»
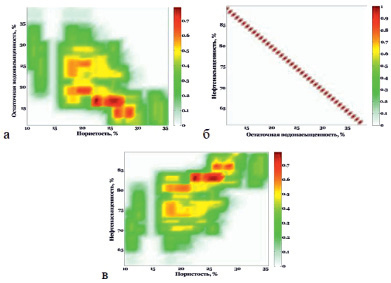
Рис. 6. Композиция нечетких отношений: а) функция принадлежности «Пористость – Остаточная водонасыщенность»; б) функция принадлежности «Остаточная водонасыщенность – Нефтенасыщенность»; в) функция принадлежности «Пористость – Нефтенасыщенность»
Результаты исследования и их обсуждение
Приведенные примеры применения аппарата нечеткого моделирования для данных Тимано-Печорской провинции показали возможность получения дифференцированного по достоверности результата. Далее построенные нечеткие петрофизические модели используются для дальнейшего прогноза и интерпретации данных скважин с целью оценки достоверности подсчета запасов.
Прогноз функции принадлежности, для итогового фильтрационно-емкостного параметра геологической модели выполняется на основе правила нечеткого логического вывода. Правило нечеткого логического вывода реализуется на основе нечеткой петрофизической модели, реализованной в форме композиции Мамдани нечеткого отношения между входным параметром и прогнозным, полученной в результате цепочки композиции отношений и функции принадлежности для исходных данных параметра, полученных на основе интерпретации данных геофизических исследований.
Построенные функции принадлежности для итогового фильтрационно-емкостного параметра, выражающие информационную обеспеченность результатов моделирования, далее используются для экспертизы – оценки достоверности по значениям функции принадлежности построенной геологической модели подсчетных параметров.
Заключение
За счет построения функции принадлежности на пространстве геологических моделей, отражающей нечеткость исходных данных и особенности нечеткой петрофизической модели, обеспечивается объективная оценка уровня информационной обеспеченности вводимых компонент геолого-геофизической модели, месторождения и возможность оптимизации дальнейших геологоразведочных работ.