Из-за сложности распределительных электрических сетей, неравномерного графика отпуска электроэнергии потребителям, развития возобновляемых источников энергии, периодические изменения схем, выполняемые для обеспечения бесперебойного питания потребителей, планирование и реализация мероприятий по повышению эффективности функционирования электрических сетей являются сложной задачей, решение которой в современных условиях невозможно без применения интеллектуальных средств автоматизации управления.
Совершенствование информационной инфраструктуры энергоснабжающих компаний, увеличение количества и пропускной способности проводных и беспроводных каналов связи упрощает организацию и повышает конкурентоспособность распределенных автоматизированных систем управления, среди прочего и перетоками реактивной электроэнергии в распределительных электрических сетях.
Использование силовых преобразователей, электронного оборудования и других нелинейных нагрузок быстро растет в промышленности, а также среди потребителей. Эти устройства характеризуются нелинейной вольт-амперной характеристикой по сравнению с традиционными нагрузками, такими как, например, резистивные нагревательные элементы. Наиболее существенными задачами повышения эффективности работы электрических сетей, включающих в себя узлы нагрузок с нелинейным характером потребления электрической энергии, являются компенсация реактивной мощности и обеспечение требуемого качества напряжения.
Из анализа мероприятий по уменьшению потерь электроэнергии и повышения ее качества в распределительных электрических сетях известно, что одним из самых эффективных способов является установление дополнительных источников реактивной мощности и управления ими [1, 2]. Последние, уменьшая токовые нагрузки линии электропередач и силовых трансформаторов, обеспечивают снижение потерь электроэнергии и повышения качества напряжения.
В промышленных электрических сетях для компенсации реактивной мощности обычно используют конденсаторные установки. Главным элементом таких комплексов является регулирующий элемент реактивной мощности, от функционального и технического исполнения которого зависит качество компенсации реактивной мощности [3, 4]. Такие регуляторы на сегодняшний день лишены интеллектуальной составляющей и не способны эффективно работать в сетях с нелинейной нагрузкой, поскольку не учитывают гармонический состав напряжения.
Исходя из вышесказанного, разработка мероприятий по компенсации реактивной мощности в современных условиях требует совершенствования существующих и разработки новых методов оптимизации и расчетных алгоритмов, которые бы учитывали не только особенности передачи электроэнергии распределительными сетями, но и эксплуатационные особенности современных источников реактивной мощности.
Современное развитие информационных технологий и вычислительных средств формирует предпосылки для применения других подходов к решению проблемы оптимизации перетоков реактивной энергии. На текущий момент методы нечеткой логики широко внедряются в промышленное производство и позволяют повышать качество регулирования в условиях неполноты информации об объекте управления [5, 6]. Именно поэтому в противопоставление к вышеописанному подходу компенсации реактивной мощности предлагается нечеткий алгоритм.
Метод теории нечеткой логики применяет вместо булевой логики экспертные оценки и использует для формирования решения совокупность нечетких функций принадлежности и правил с несколькими выводами, позволяющие сформировать базу знаний системы [7, 8]. При этом на основе экспертных знаний определяются терм-множества параметров, нечеткого регулирования [9, 10].
Цель исследования: разработка схемы и нечеткого алгоритма компенсации реактивной мощности в электрической сети с устройствами нелинейного характера потребления электроэнергии, а также его тестирование на базе программного комплекса «МATLAB».
Материалы и методы исследования
При разработке описываемого алгоритма управления реактивной мощностью в сети с нелинейными потребителями использовались математический инструментарий нечеткой логики и метод имитационного моделирования предложенных решений на базе 14-узловой схемы IEEE [11]. Осуществлен анализ результатов компьютерного моделирования.
Результаты исследования и их обсуждение
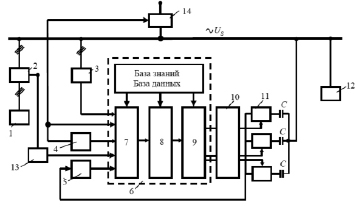
Рис. 1. Структурная схема нечеткого регулятора реактивной мощности
Разработанный нечеткий регулятор реактивной мощности представлен на рис. 1 и описан в виде структурных блоков:
1 – активная нагрузка;
2 – датчик реактивной мощности;
3 – датчик величины напряжения на питающей линии;
4 – скорость изменения реактивной мощности;
5 – счетчик количества переключений, совершаемых за день;
6 – нечеткий регулятор;
7 – блок фаззификации, используемый для преобразования четких сигналов Q, Q’, U, KU, N в нечеткие множества μQ, μQ’, μU,μKU, μN. При этом Q, Q’, U, KU, N – реактивная мощность, вычисленное значение производной реактивной мощности, величина напряжения, коэффициент гармонических составляющих напряжения и количество выполняемых переключений соответственно, а μQ μQ’ μU μKU μN – функции принадлежности, которые соответствуют данным параметрам;
8 – блок нечеткого вывода (совокупность продукционных правил системы);
9 – блок дефаззификации;
10; 11 – база функций принадлежности нечетких множеств, входные эти сигналы и набор нечетких продукционных правил;
12 – коммутирующий блок;
13 – нагрузка нелинейнего характера;
14 – показатели несинусоидальности напряжения (датчик).
Нечеткий регулятор реактивной мощности функционирует по следующему принципу. Параметры процесса, также величина переключений секций батарей статических конденсаторов N в виде четких сигналов поступают на нечеткий регулятор. Интерпретированные в фаззификаторе сформированные нечеткие множества поступают в механизм нечеткого логического вывода [12]. Нечеткие множества находятся следующим образом:
F = fuzzifier (Q, Q’, U, KU, N), (1)
где Q, Q’, U, KU, N – совокупность четких сигналов, описанных выше;
F – результат фаззификации;
fuzzifier – оператор, позволяющий осуществить операцию фаззификации.
После этапа фаззификации необходимо обработать лингвистические выходные переменные, которые должны быть переведены в четкое значение. Цель состоит в том, чтобы получить управляющее воздействие, которое наилучшим образом соответствует полученным нечетким значениям лингвистических переменных. Для этого используется операция дефаззификации – обратного преобразования, которое выводит результат из нечеткой области обратно в четкие значения. Текущий метод формирует суммарный выход, учитывая все элементы результирующего нечеткого множества с соответствующими весами.
Регулирование потоков реактивной мощности в электрической сети с нелинейной нагрузкой реализовано программным образом. Блок-схема данного алгоритма, представлена на рис. 2. Параметры от датчиков, значение производной реактивной мощности (Q′), а также число совершаемых переключений секций батарей статических конденсаторов за день при увеличении коэффициента KU выше нормы, поступают на блок нечеткого механизма принятия решения.
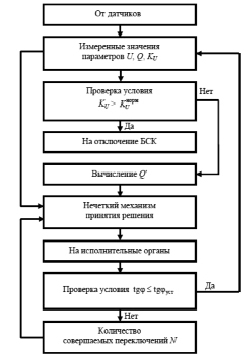
Рис. 2. Нечеткий алгоритм компенсации реактивной мощности
Решение переключения формируется с учетом текущих значений выходного вектора состояний секций с выдержкой времени в зависимости от числа выполняемых переключений и динамики изменения реактивной мощности. При невыполнении условия KU >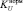 
происходит отключение секций батарей статических конденсаторов. При выполнении условия происходит отключение секций батарей статических конденсаторов. При выполнении условия tg? ≤ tg?уст работа нечеткого регулятора завершается, где tg? и tg?уст – текущее и установленное значения коэффициента реактивной мощности соответственно.
Предлагаемый алгоритм был протестирован в программе «MATLAB», в комплексе «Simulink» на базе 14-узловой схемы IEEE (рис. 3). Испытательная схема включает в себя 14 шин, 5 генераторов и 11 нагрузок.
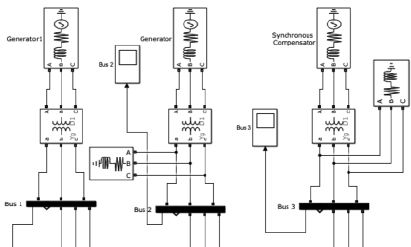
Рис. 3. Фрагмент 14-узловой схемы IEEE в «MATLAB»
Полученные диаграммы нечеткого управления реактивной мощностью (а) и tg? (б) изображены на рис. 4 (® – исходный режим, ¡ – режим с импользованием нечеткого регулирования, p – режим с учетом KU).
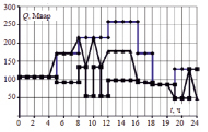
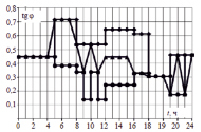
а) б)
Рис. 4. Результаты моделирования предложенных решений (диаграмма реактивной мощности (а) и tg? (б))
Как видно из рис. 4, в соответствии с управлением при учете значения гармонических составляющих напряжения нечеткий регулятор формирует управляющие сигналы только при его малых значениях и значениях, находящихся в пределах нормы. При управлении значения tg? в некоторые моменты времени (например, в период 4–7 ч. tg? = 0,71) получаются выше нормы. Но, несмотря на это, даже если гармонические составляющие напряжения выше нормы, предотвращаются перегрузка батарей статических конденсаторов.
Данные методы могут качественным образом повлиять на срок службы конденсаторной батареи, а также снизить количество мероприятий по осуществлению текущего и капитального ремонтов по отношению к ней. Уменьшается вероятность отказа конденсаторной батареи и повышается надежность при эксплуатации.
Заключение
Таким образом, на базе математического аппарата нечеткой логики предложен алгоритм нечеткого регулирования реактивной мощности в электросети с нелинейными потребителями электрической энергии. Данное решение дает возможность поддерживать коэффициент реактивной мощности tg? в рамках, регламентируемых в технических условиях для потребителей, а также может применяться для обеспечения нормального эксплуатационного состояния батарей статических конденсаторов.