Текущее развитие мировой экономики ведет к ужесточению экономической конкуренции как между странами, так и между отдельными регионами. Мировые производители стараются перенести свои основные производственные фонды (ОПФ) в любую точку нашей планеты с наиболее выгодными для них условиями (с точки зрения прибыли) производства, происходит процесс глобализации экономики с переносом загрязняющих предприятий в развивающиеся страны. В этом процессе экологические риски не всегда учитываются в полной мере как в угоду целям собственно экономического развития, так и в силу особенностей эколого-экономической политики конкретных регионов [1]. В этой связи задача оценки инвестиционной привлекательности (климата) региона или любой территории, на которой осуществляется масштабное производство, негативно воздействующее на окружающую природную среду (ОПС), является актуальной в свете необходимости учета интересов проживающего населения. Помимо рисков производственного, инвестиционного, финансового, социального и другого характеров для участников эколого-экономического процесса на территории практически всегда возникают экологические риски. Например, для регионального управляющего центра (РУЦ) в качестве экологических рисков его деятельности могут выступать необходимость осуществления затрат на поддержку социальных, медицинских, экологических программ, направления средств на строительство больниц, закупку лекарств, восстановление экосистем, развитие экологически чистого производства, а для производителя (инвестора) при запуске проектов, предполагающих ухудшение экологии, – необходимость вложений в очистные сооружения, затрат на установку и использование наилучших доступных технологий (НДТ) с целью снижения негативного воздействия на ОПС [2]. Для улучшения эколого-экономического климата необходимо использовать механизмы комплексного оценивания уровня экологических рисков с учетом оценки производственного потенциала производителя. Классический подход к оцениванию экологических рисков основан на учете потенциального ущерба от реализации рискового экологического события и вероятности его возникновения, которая в большинстве случаев определяется статистическим или экспертным методом [3]. Отечественный и зарубежный опыт в области разработки механизмов снижения экологических рисков можно разделить на следующие классы [4]: механизмы экономической ответственности (система нормативов, квот, отклонение от которых приводит к наложению штрафов), механизмы стимулирования снижения уровня риска (льготы налогообложения, кредитования природоохранных мероприятий), механизмы перераспределения риска (государственное, независимое, взаимное страхование), механизмы резервирования (формирование материальных, трудовых ресурсов, мощностей на случай чрезвычайных ситуаций), механизмы формирования и распределения специальных фондов и механизмы управления региональными программами, которые задействуют все механизмы, включая в том числе механизмы согласования интересов органов власти [5]. Целью данной работы является изложение системного подхода к оценке эколого-инвестиционной привлекательности региона, включающего концепцию, математическую модель, ориентированную на ее использование в автоматизированной системе поддержки принятия управленческих решений как управляющим центром, так и производителем [6, 7].
Материалы и методы исследования
Определим понятие эколого-экономической привлекательности территории как некоторую совокупность факторов, учитывающую взаимодействие ее экономического потенциала и возникающих при функционировании территории экологических рисков. Предположим, что эколого-экономическая политика в регионе разрабатывается региональным управляющим центром, заинтересованным в эффективном функционировании региона, как эколого-экономической системы. Предположим также, что необходимо организовать взаимодействие РУЦ и производителя, которое будет способствовать эколого-экономической привлекательности региона. Следуя поставленному требованию развития региона, количественно определим риски, возникающие при таком развитии, как финансовые потери из-за неправильно поставленной или недостигнутой стратегической цели эколого-экономического развития. В качестве стратегических целей для РУЦ будем рассматривать максимизацию объективно обусловленных экономическим потенциалом производителя налоговых платежей, включающих экологические платежи, а для производителя – максимизацию NPV (чистой приведенной стоимости) проекта по производству продукции или направления экономической деятельности, с учетом ограничений своего функционирования (экологических, производственных инвестиционных, финансовых и т.д.). При этом для численной оценки риска необходимо перейти от натурального выражения объемов производства (определяющих объемы загрязняющих выбросов) к финансовому (денежному) [8], такому как, например, стоимостные затраты на восстановление работоспособности системы при реализации выбранных рисков. Для достижения цели исследования построим оптимизационную математическую модель эколого-экономической привлекательности региона. Результатом формирования эколого-экономической политики предполагается получение такого оптимального распределения имеющихся потенциальных инвестиций и объемов производимой в регионе продукции n видов, а также значений коэффициента экологического платежа, при которых решена многокритериальная задача максимизации их суммы для РУЦ и максимизации чистой приведенной стоимости (NPV) проекта для производителя. Предположим, кроме того, что в регионе заданы (найдены) зависимости рисков ri = fi(x) кризисного развития системы в i-м направлении (i = 1,…,m; m – количество направлений) обеспечения экологической, экономической, финансовой и других видов безопасности от вектора затрат х?Rl (l – количество статей затрат) на их избежание (устранение, исключение, уменьшение) [9]. Отметим, что при математическом моделировании деятельности производителя традиционно учитывается часть рисков функционирования региона (например, к ним относятся риски инфляции, неплатежеспособности и/или недофинансирования производителя, риски недопроизводства и/или перепроизводства продукции).
В связи с необходимостью практической программной реализации решения поставленной задачи и учитывая большую размерность задачи и множество ее ограничений [10], для оперативной поддержки принятия управленческого решения РУЦ будем считать, что зависимость функций fi от x линейна, а именно fi = ai – bix. Линейность функций fi позволяет строить оптимизационные модели эколого-экономического взаимодействия РУЦ и производителя с выходом на создание СППР. Предположим, что:
1) каждый вид продукции производится с помощью одного комплекта ОПФ, т.е. выполняется принцип «чистых отраслей»;
2) рассматриваются два участника взаимодействия – РУЦ и производитель;
3) РУЦ и производитель располагают либо собственными, либо заемными (дотационными) средствами для финансирования своей деятельности (либо избежания/устранения своих рисков);
4) учитываются лишь те виды налогов и сборов, которые зависят от искомых объемов инвестиций и производства продукции: налог на добавленную стоимость (НДС), страховые взносы в социальные фонды (СВ), налог на имущество (НИ), налог на прибыль (НП), экологические платежи и другие);
5) ОПФ, используемые при производстве, загружены максимально, т.е. имеют максимальную фондоотдачу.
Результаты исследования и их обсуждение
Модифицируем представленную в работе [11] математическую постановку изложенной выше задачи с учетом цели текущей работы. Пусть n – количество видов производимой продукции и, в соответствии с принципом «чистых отраслей», комплектов основных производственных фондов (ОПФ), xk = ckmk – оптимальные суммы инвестиций в ОПФ k-го вида, где ck – стоимость k-го ОПФ, mk – оптимальное количество единиц ОПФ k-го вида, xn+k = Pkmkyk – оптимальная выручка от продажи продукции k-го вида (k = 1,…,n), где Pk – стоимость единицы продукции k-го вида, yk – оптимальный объем продукции, произведенной комплектом ОПФ k-го вида, x2n+1 – оптимальная сумма кредитов, x2n+2 – оптимальная сумма дотаций на осуществление текущей деятельности производителя, x2n+2+l (l = 1,…,L) – оптимальные затраты на предотвращение l-го риска производителя, L – количество рисков производителя, x2n+2+L+m (m = 1,…,M) – оптимальные затраты на предотвращение m-го риска РУЦ, M – количество рисков РУЦ; ak, dk – максимальные издержки, которые несут соответственно производитель и РУЦ в случае отсутствия затрат на k-м рисковом направлении своего функционирования; bk, ek – задаваемые экспертно коэффициенты, имеющие смысл соответственно для каждого производителя и РУЦ, оценки значимости эффекта от осуществленных затрат на k-м рисковом направлении своего функционирования, Vk, Tk – производительность, срок полезного использования k-го ОПФ; 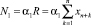 – налог на добавленную стоимость (НДС) за год,
– налог на добавленную стоимость (НДС) за год, 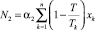 – налог на имущество (НИ) за год, N3 = α3Wb – налог на прибыль (НП) за год,
– налог на имущество (НИ) за год, N3 = α3Wb – налог на прибыль (НП) за год, 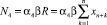 – страховые взносы в социальные фонды (СВСФ)
– страховые взносы в социальные фонды (СВСФ) 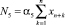 – дополнительные затраты (ДЗ) производителя, зависящие от объемов производства (например, налог на добычу полезных ископаемых); αi, i = 1,…,5 – соответственно ставки НДС, НИ, НП, СВСФ и ДЗ;
– дополнительные затраты (ДЗ) производителя, зависящие от объемов производства (например, налог на добычу полезных ископаемых); αi, i = 1,…,5 – соответственно ставки НДС, НИ, НП, СВСФ и ДЗ; 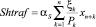 – сумма экологического платежа за год, αS – коэффициент экологического платежа, ξk – удельный выброс загрязнителя на единицу продукции k-го вида; T – горизонт планирования эколого-экономического проекта; r – годовая ставка дисконтирования инвестиционного проекта, учитывающая инфляцию, уровень требований инвестора и другие экономические и политические риски деятельности производителя;
– сумма экологического платежа за год, αS – коэффициент экологического платежа, ξk – удельный выброс загрязнителя на единицу продукции k-го вида; T – горизонт планирования эколого-экономического проекта; r – годовая ставка дисконтирования инвестиционного проекта, учитывающая инфляцию, уровень требований инвестора и другие экономические и политические риски деятельности производителя; 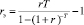 – эффективная ставка дисконтирования, учитывающая динамические особенности критериев эффективности в предположении постоянства потоков прибыли и амортизации на всем горизонте планирования; qk – стоимостной спрос на продукцию k-го вида, zk – оборотные затраты на производство продукции k-го вида; δk – фондоотдача (эффективность, мощность) ОПФ k-го вида, Dk – предельно допустимые выбросы (ПДВ) загрязнителя от производства k-й продукции, θk – удельные оборотные затраты (на единицу продукции) производителя; DS0 – собственные начальные средства производителя; Cr – оптимальный поток кредитования текущей деятельности производителя, r0 – ставка кредита на финансирование текущей деятельности, T0 – срок кредита на финансирование текущей деятельности, Crmax – максимально возможный размер годового кредита, взятого на финансирование текущей деятельности, Dotmax – максимально возможная сумма годовых дотаций производителю, Imax – максимально возможная сумма инвестиций производителя, L1, L2 – соответственно максимальные суммы затраты на избежание (устранение) всех выделенных рисков производителя и РУЦ.
– эффективная ставка дисконтирования, учитывающая динамические особенности критериев эффективности в предположении постоянства потоков прибыли и амортизации на всем горизонте планирования; qk – стоимостной спрос на продукцию k-го вида, zk – оборотные затраты на производство продукции k-го вида; δk – фондоотдача (эффективность, мощность) ОПФ k-го вида, Dk – предельно допустимые выбросы (ПДВ) загрязнителя от производства k-й продукции, θk – удельные оборотные затраты (на единицу продукции) производителя; DS0 – собственные начальные средства производителя; Cr – оптимальный поток кредитования текущей деятельности производителя, r0 – ставка кредита на финансирование текущей деятельности, T0 – срок кредита на финансирование текущей деятельности, Crmax – максимально возможный размер годового кредита, взятого на финансирование текущей деятельности, Dotmax – максимально возможная сумма годовых дотаций производителю, Imax – максимально возможная сумма инвестиций производителя, L1, L2 – соответственно максимальные суммы затраты на избежание (устранение) всех выделенных рисков производителя и РУЦ.
Используя представленные в [11] алгоритмы расчета потоков доходов и расходов производителя, имеющие линейную зависимость от искомых переменных модели, сформулируем следующую математическую модель эколого-инвестиционной привлекательности добывающей территории в форме двухкритериальной задачи линейного программирования.
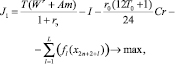 (1)
(1)
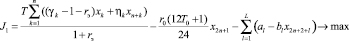 , (1’)
, (1’)
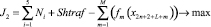 , (2)
, (2)
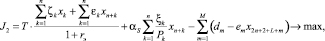 (2’)
(2’)
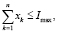 (3)
(3)
xn+k ≤ δk xk , (4)
xn+k ≤ qk , (5)
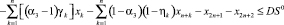 , (6)
, (6)
x2n+1 ≤ Crmax, (7)
x2n+2 ≤ Dotmax, (8)
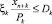 , (9)
, (9)
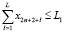 , (10)
, (10)
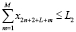 , (11)
, (11)
xm ≥ 0 (m = 1,…, 2n + 2 + L + M), (12)
где
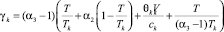 ,
,
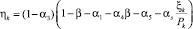 ;
;
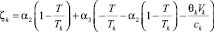 ;
;
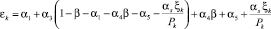 ;
;
(1), (1’) – критерий производителя (содержательный и математический вид соответственно), представляющий собой сальдо дисконтированной по ставке rэ суммы прибыли и оценки имущества, а также осуществленных инвестиций на рассматриваемом горизонте планирования; (2), (2’) – критерий управляющего центра (содержательный и математический вид соответственно), означающий максимизацию поступающих в бюджет территории сумм налогов и платежей за нарушение экологических норм; (3) – условие ограниченности максимальных инвестиций; (4) – условие ограниченности выручки от продажи продукции фондоотдачей (эффективностью, мощностью) ОПФ; (5) – условие ограниченности выручки от продажи продукции спросом на продукцию, (6) – условие неотрицательности суммы собственных средств производителя, гарантирующее его платежеспособность на всем горизонте планирования; (7) – условие ограниченности максимальных годовых кредитов; (8) – условие ограниченности максимальных годовых дотаций; (9) – условие ограниченности выбросов загрязняющих веществ объемами предельно допустимых выбросов (ПДВ); (10) – условие ограниченности суммарных затрат на устранение рисков производителя; (11) – условие ограниченности суммарных затрат на устранение рисков РУЦ; (12) – условие неотрицательности значений искомых переменных модели.
Несложно установить, что задача, описываемая математической моделью (1)–(12), имеет решение, так как допустимое множество представляет собой непустой (содержит тривиальное решение), ограниченный компакт. Наличие нетривиального решения, на модельных данных, было показано с использованием пакета [12].
Выводы
Таким образом, предложенная математическая модель описывает инвестиционную, производственную и финансовую деятельность производителя с учетом экологических факторов, основные стратегические потоки РУЦ и регионального производителя и содержит такие искомые переменные, как оптимальные объемы инвестиций, производства, кредитов, дотаций, предотвращения рисков и имеет решение для всех значений входящих в нее параметров. Наличие групп переменных, учитывающих затраты на устранение рисков, в рамках представленной постановки, позволяет рассматривать модель (1)–(12) как модель эколого-инвестиционной привлекательности территории. Данная математическая модель может быть реализована в СППР для принятия эффективных эколого-инвестиционных решений как региональным управляющим центром, так и производителем.
Статья подготовлена в рамках выполнения научно-исследовательской работы по теме: «Эколого-экономический механизм функционирования минерально-сырьевых кластеров для обеспечения устойчивого развития добывающих регионов» (приказ ФГБОУ ВО «Российский экономический университет им. Г.В. Плеханова» № 637 от 08.05.2018).
Раздел «Методы исследования» данной статьи подготовлен при поддержке Департамента образования и науки Кемеровской области в рамках Соглашения о грантах из регионального бюджета на осуществление исследовательских проектов (проект «Интеллектуальная собственность как основа устойчивого развития угледобывающего региона (на примере Кемеровской области)»). Соглашение № 21 от 14.08.2018 г.



