Хорошо известно, какую роль в радиотехнике, электронике, теории управления и других технических науках играют периодические процессы. Как правило, эти процессы являются рабочими режимами функционирования технических систем, а следовательно, должны обладать свойством устойчивости, т.е. притягивать к себе другие режимы – переходные процессы. Математическими образами периодических процессов часто выступают замкнутые траектории (циклы) в соответствующем фазовом пространстве – пространстве состояний математической модели. Если такие циклы изолированы, то они называются предельными. Если циклы притягивают к себе соседние траектории при t > + ∞, то они называются устойчивыми предельными циклами, если отталкивают, то неустойчивыми. Именно устойчивые предельные циклы выступают образами устойчивых автоколебаний в физической системе. Из сказанного вытекает актуальность задачи нахождения как устойчивых, так и неустойчивых циклов, а также анализ зависимости поведения динамических систем в целом от параметров [1, 2]. Последние вопросы связаны с исследованием бифуркаций в динамических системах [3]. Так, например, на рис. 1 приведена последовательность фазовых картин некоторой физической системы, зависящей от параметра α. Видно, что разным значениям параметра α могут отвечать принципиально различные фазовые картины – а следовательно, и поведение физической системы.
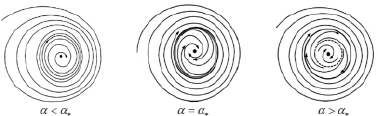
Рис. 1. Бифуркация рождения устойчивого цикла из сгущения траекторий
Ясно и теоретически хорошо изучено, что если в системе несколько циклов, то все они одновременно не могут являться устойчивыми, так как траектория, «наматывающаяся» на некоторый цикл при t > + ∞, автоматически должна «сматываться» с некоторого цикла, который в свою очередь будет неустойчивым. Отметим, что устойчивым предельным циклам отвечает в физической системе автоколебательный процесс. В данной статье рассматривается автономное дифференциальное уравнение второго порядка, являющееся математической моделью генератора автоколебаний [1, 4]
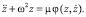(1)
Здесь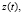 
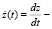динамические переменные, определяющие состояние генератора, 
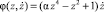– функция обратной связи, μ – безразмерный положительный параметр, отвечающий за подкачку энергии в систему от внешнего источника (параметр возбуждения), α,ω2 – положительные безразмерные параметры генератора. Уравнение (1) при μ = 0 совпадает с уравнением гармонического осциллятора, при μ > 0, α = 0 – с классическим уравнением Ван-дер-Поля - генератора с контуром в цепи анода или сетки. Известно, что на фазовой плоскости 
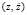уравнения Ван-дер-Поля имеется единственный устойчивый предельный цикл, которому с физической точки зрения отвечает устойчивый автоколебательный процесс. Уравнение (1) при α ≠ 0 обобщает уравнение Ван-дер-Поля на случай иной аппроксимации нелинейной характеристики обратной связи [4]. Целью настоящей статьи является качественно-численное изучение математической модели генератора колебаний (1) в зависимости от параметров модели. Ее результаты могут быть полезны при теоретическом анализе и экспериментальном исследовании функционирования систем управления в различных условиях с целью улучшения их эксплуатационных характеристик. Учитывая, что заменой времени параметр ω можно сделать равным единице, будем в дальнейшем считать ω = 1.
Метод Ван-дер-Поля
1. Для начала для уравнения (1) на плоскости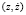 
рассмотрим положительно-определенную функцию Ляпунова 
, (
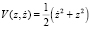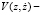полная энергия системы) производная, от которой, вычисленная в силу уравнения (1), имеет вид
.
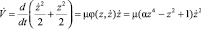Легко видеть, что при всех z,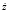 
и всех значениях параметров α > 0,25 и μ > 0 функция 
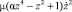неотрицательна. Отсюда вытекает, что z = 0, 
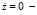неустойчивое в целом положение равновесия [5] осциллятора (1) и, следовательно, в области α > 0,25 устойчивые колебания в системе, описываемой уравнением (1), невозможны.
2. Предположим теперь, что 0 < α < 0,25,а μ – малый параметр. Тогда уравнение (1) квазилинейно и можно применить, например, для его исследования метод Ван-дер-Поля – частный случай более строгого метода – метода усреднения [6]. С этой целью в (1) сделаем замену переменных по формулам: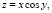 
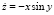. В переменных x, y уравнение (1) запишется в виде эквивалентной системы
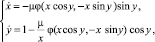(2)
правые части которой являются 2π – периодическими функциями по фазе y.
От точной системы (2) перейдем к приближенной системе так называемых укороченных уравнений
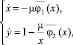(3)
где правые част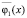и 
и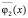 
являются осредненными по периоду функциями
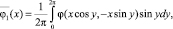
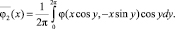
В системе (3) первое уравнение позволяет приближенно определить значения стационарных амплитуд колебаний. Эти амплитуды находятся из конечного уравнения
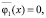(4)
которое в нашем случае принимает вид
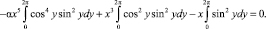
Вычисляя интегралы
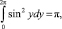
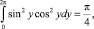
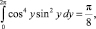
окончательно приходим к уравнению: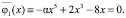 
Отсюда находим, что при 0 < ? < 0,125 его корнями будут (амплитуды стационарных колебаний):
.
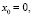
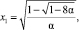
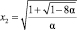На рис. 2 и в таблице соответственно изображены графики и приведены значения функций x1 = x1(α), x2 = x2(α). Видно, что при α = 0,125 величина x1 = x2. Последнее равенство будет отвечать слипанию на фазовой плоскости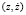 
уравнения (1) устойчивого и неустойчивого циклов, т.е. бифуркации полуустойчивого цикла. Заметим, также, что 
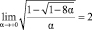, что согласуется с известным фактом: для классического уравнения Ван-дер-Поля для малых значений параметра μ амплитуда x1 = 2 [6, 7].
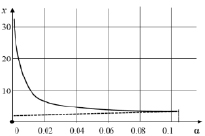
Рис. 2. Графики функций x1 = x1(α), x2 = x2(α) (сплошная кривая отвечает амплитуде неустойчивого колебания, пунктирная – амплитуде устойчивого колебания)
Для определения амплитуд, отвечающих устойчивому и неустойчивому колебаниям, вычислим производную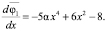 
Учитывая очевидные неравенства
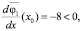
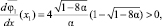
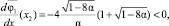
заключаем, что при 0 < α < 0,125 в системе возможен лишь один автоколебательный режим со стационарной амплитудой x = x1. Стационарный режим с амплитудой x = x2 является, очевидно, неустойчивым, т.е. физически нереализуемым. Кроме того, напомним, что положение равновесия x0 = 0 является также неустойчивым.
|
α |
Амплитуда устойчивого цикла x1 |
Амплитуда неустойчивого цикла x2 |
|
0 |
2 |
∞ |
|
0,0001 |
2,0002 |
141 |
|
0,001 |
2,002 |
44 |
|
0,01 |
2,02 |
14 |
|
0,1 |
2,35 |
3,809 |
|
0,105 |
2,39 |
3,65 |
|
0,11 |
2,44 |
3,498 |
|
0,12 |
2,58 |
3,16 |
|
0,125 |
|
|
Моделирование траекторий на фазовой плоскости
Для визуализации динамических процессов в автогенераторе дадим численное представление его траекторий на плоскости 
и решений (интегральных кривых) на плоскости (t, z) c использованием программы WinSet [8, 9]. На рис. 3 изображены устойчивый (внутренний) и неустойчивый (внешний) циклы уравнения (1). Для построения неустойчивого цикла использовалось интегрирование в обратную сторону по времени. При этом движение изображающих точек происходит естественно против часовой стрелки. При вычислениях были взяты следующие значения параметров: μ = 0,1, α = 0,105, ω2 = 1. Внешний цикл образует границу притяжения устойчивого – внутреннего цикла. На рис. 4 на плоскости (t, z) изображены соответствующие интегральные кривые, отвечающие переходному процессу.
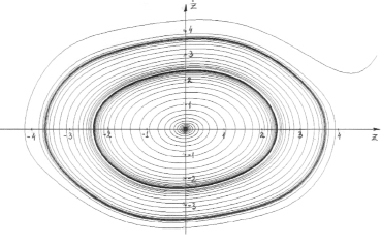
Рис. 3. Предельные циклы на фазовой плоскости (внутренний цикл – устойчивый, внешний – неустойчивый)
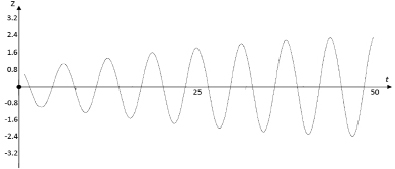
а)
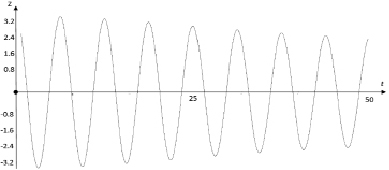
б)
Рис. 4. Возбуждение генератора: a) при малой начальной энергии; б) при большой начальной энергии
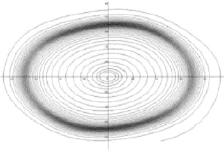
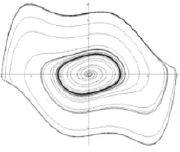
а) б)
Рис. 5. Фазовые портреты: а) полуустойчивый цикл (α = 0,125); б) устойчивый и неустойчивые циклы (μ = 0,3, α = 0,05)
На рис. 5, а, изображен фазовый портрет полуустойчивого цикла – цикла, который получается от слияния устойчивого и неустойчивого циклов при α = 0,125.
Замечание 1. В области параметра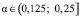 
, как уже отмечалось, уравнение 
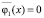имеет единственный корень х0 = 0, которому отвечает неустойчивое в целом положение равновесия z = 0, 
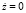уравнения (1). Заметим, что рассмотренная нами функция Ляпунова эту область параметра не определила.
Замечание 2. Современные средства визуализации позволяют оценить и влияние параметров на форму колебаний. На рис. 5, б, приведен фазовый портрет уравнения (1) для других значений параметров. Видно, что отклонение от малых значений параметра μ оказывает сильное влияние на форму колебаний.
Заключение
Рассмотренная выше математическая модель описывает мягкий режим возбуждения генератора колебаний. Однако если в уравнении (1) знак при функции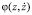 
изменить на противоположный, то придем к модели, описывающей жесткий режим возбуждения колебаний, при этом циклы сменят естественно свою устойчивость. При этом положение равновесия в начале координат будет устойчивым, внутренний цикл будет неустойчивым, внешний – устойчивым. В этом случае для возбуждения генератора необходима дополнительная энергия, забрасывающая динамические переменные 
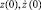генератора в область, находящуюся за неустойчивым циклом [9]. В уравнении (1) характеристика 
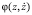обладала свойствами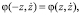 
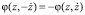. Однако проведенные рассуждения можно провести и для более общего случая, например отказавшись при малом μ от первого предположения – симметрии «коэффициента трения» αz4 – z2 + 1. Кроме того, при немалых значениях параметра μ, используя программу Winset, можно исследовать эффекты релаксации, сказывающиеся в наличии быстрых и медленных движений в автогенераторе, что аналитическими методами сделать затруднительно.
Использованный выше метод Ван-дер-Поля носит эвристический качественный характер и применим для колебательных систем только с одной степенью свободы. Его развитие и распространение на многомерные системы было сделано Н.М. Крыловым, Н.Н. Боголюбовым и Ю.А. Митропольским. Использование этого метода в рассмотренной выше задаче позволило бы построить асимптотические представления для решений и указать их точность, но это может быть предметом другого исследования.