Исследованию тепло-массообмена между каплей и окружающей средой посвящены работы [1–3]. В работе [1] предполагается, что число Пекле Pe большое, а константа скорости объёмной химической реакции значительно меньше. Исследованию теплообмена с внутренними пограничными слоями посвящена работа [2]. При больших значениях константы скорости объёмной химической реакции (одного порядка с числом Пекле) основное изменение концентрации происходит вблизи поверхности капли [4, с. 77–83].
Рассмотрим стационарную диффузию внутри сферической капли радиуса a, обтекаемой поступательным потоком вязкой несжимаемой жидкости со скоростью U0 вдали от капли при малых числах Рейнольдса в случае, когда вещество, диффундирующее внутри капли, испытывает химическое превращение. Распределение концентрации c(r, θ) в безразмерных переменных удовлетворяет уравнению [3, с. 198]
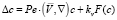(1)
поле скоростей соответствует сферическому вихрю Хилла [5] и определяется из выражений
,
,
,
, 
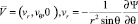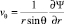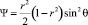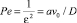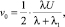
где Pe – число Пекле; D – коэффициент диффузии вещества; λ и λ1 – динамические вязкости жидкостей вне и внутри капли; kv – константа скорости объемной химической реакции; Δ – оператор Лапласа; Ψ(r, θ) – функция тока; r, θ – сферические координаты (φ – const). Требуется найти асимптотику решения уравнения (1), удовлетворяющего граничному условию
c = 1 при r = 1. (2)
Будем считать, что функция F(u) удовлетворяет условиям
, 
,
, 
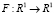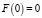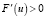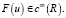(3)
Цель работы состоит в построении асимптотического разложения решения задачи (1), (2) для больших чисел Пекле Pe в малой окрестности капли. Решение строится методом согласования асимптотических разложений.
Для решения задачи (1), (2) область внутри капли разбивается на несколько областей (эти области указаны на рисунке). В каждой области вводятся новые независимые переменные (см., напр., ниже пункт диффузионный пограничный слой, пункт эллиптический пограничный слой) затем уравнение (1) записывается в этих переменных, и находят такие решения полученных уравнений, которые сращиваются на границах области и удовлетворяют граничным условиям. В этом состоит идеология метода согласования (сращивания) асимптотических разложений.
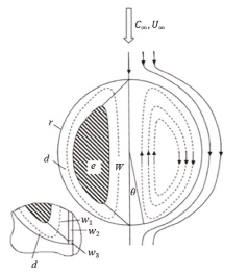
Структура поля концентрации внутри капли: е – ядро потока, d – область диффузионного пограничного слоя, W – область диффузионного следа, w1 – конвективно-погранслойная область диффузионного следа, w2 – внутренняя область диффузионного следа, w3 – область задней критической точки, r, θ – сферические координаты, r = 1 – соответствует поверхности капли
При построении асимптотики удобно ввести малый параметр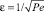 
. Уравнение (1), с учетом обозначений и μ = kv/Pe, перепишем в виде
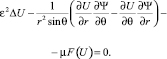(4)
Известно [3], что в предельных случаях Pe >> 1, kv – const, и Pe – const, kv >> Pe решение задачи (1), (4) упрощается. В первом случае, Pe >> 1, kv – const, задача исследована в работе [3, с. 196–205]. В данной работе предполагается, что Pe > ∞, kv > ∞ (или достаточно большие), а величина μ0 = kv/Pe – постоянная. При таких же предположениях, но в случае объемной химической реакции первого порядка (F(u) ≡ u) асимптотика внутри капли исследована в работе [4, с. 77–83]. Задача вне капли исследовалась в работе [6], а вне цилиндра в работе [7]. В работах [8, 9] обсуждаются качественные особенности реакционно-диффузионных дифференциальных уравнений с запаздыванием.
Асимптотический анализ уравнения (1) показывает, что внутри капли можно выделить ядро потока е: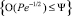
, область диффузионного пограничного слоя d:
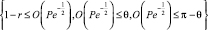
и область диффузионного следа W:
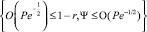(рисунок).
В случае Pe >> 1, kv – const, задача в области е исследована в работе [3, с. 196–205]. В данной работе задача исследована в областях d, w3, когда числа Pe >> 1, kv >> 1, а их отношение ограничено (именно этот наиболее трудный случай исследован в работе [4], линейный случай). В данной работе рассмотрен случай, когда функция F(u) – нелинейная. В этом состоит новизна работы.
Диффузионный пограничный слой
Асимптотика решения задачи (1), (2) в диффузионном пограничном слое d строится в переменных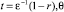 
, решение ищется аналогично [7] в виде ряда
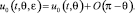(5)
Функцию F(u) заменим главными членами разложения в окрестности u0(x, θ), функцию тока Ψ разложим в ряд около границы. Подставим полученные выражения, а также ряд (5) в уравнение (4), приравниваем коэффициенты при одинаковых степенях ε. Тогда для определения u0(t, θ) в области < θ < π, 0 < t получаем краевую задачу
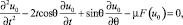(6)
u0(0, θ) = 1; u0(t, θ) → 0 при t → ∞. (7)
Уравнение (6) – это вырождающееся параболическое уравнение при θ = 0, θ = π.
Алгоритм построения решения состоит в следующем. Сначала находим формальное решение в окрестности линии вырождения θ = π в виде ряда по четным степеням (π – θ)2 с коэффициентами, зависящими от t. Коэффициенты строятся как решения системы обыкновенных дифференциальных уравнений
,
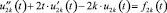где k = 0, 1, 2,...
Затем легко получить оценку
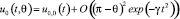
для некоторого γ > 0, и отсюда следует оценка
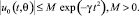
В области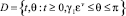 
для некоторого
.
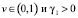Из условий (2) и из условий симметрии получим граничные условия
при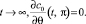 
(8)
Структура асимптотики функции u(0)(t, θ) при θ > 0 различна для малых и больших значений Ψ. При малых Ψ асимптотическое разложение строится в переменных t, θ, а при значениях, отделенных от нуля, в переменных Ψ0, τ, где
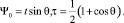
Для определения коэффициентов главного члена асимптотического разложения при θ → 0, учитывая, что u(0)(t, θ) ищется в виде u0(t) + o(θ), получаем уравнение вида
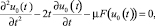(9)
с условиями
u0(0) = 1; u0(t) > 0 при t → ∞. (10)
Аналогично работе [6] сформулируем теорему.
Теорема. Пусть F(u) удовлетворяет условию (3) и разлагается в ряд
,
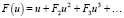тогда существует решение задачи (9)–(11), такое, что при t > + ∞ решение задачи (9)–(10) имеет следующее асимптотическое представление
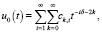(11)
где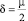 
и ck,i следующие:
, 
,
,
,
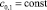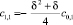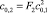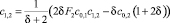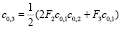, … (12)
В работе [6] коэффициенты ck,i найдены численно. Коэффициент c0,1 при главном члене выбирается так, что построенное решение удовлетворяет первому из граничных условий (10).
В уравнении (7) путем разложения функции F(u(0)) в ряд Тейлора с остаточным членом линейную часть оставим в левой, а остальные перенесем вправо. Тогда получим следующее уравнение
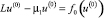, (13)
,
,
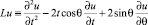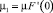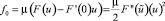. (14)
Для удобства положим F’(0) = 1.
В уравнении (13) сделаем следующую замену функции и переменных [7, с. 8–12]
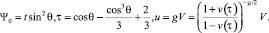(15)
Тогда уравнение (13) примет вид
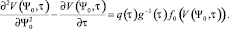(16)
где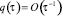 
для 
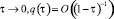при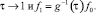 
А граничные условия имеют вид
, 
, 
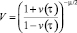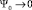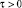, (17)
V > 0 при Ψ0 → ∞, (18)
, 
, 
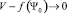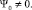(19)
Рассмотрим вспомогательную задачу при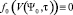 
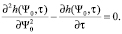
Тогда функция h(Ψ0, τ) при условиях (17)–(19) (для h(Ψ0, τ)) описывается выражением
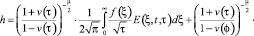
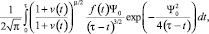
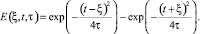(20)
Формула (20) получена в работе [5] в случае обтекания капли, когда функция F(u) линейна. Отсюда получаем, что формула (20) является главным членом разложения решения задачи (16)–(19), тогда для достаточно малого ε и некоторых δ > 0, γ0 > 0 получаем
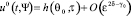
при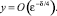 
(21)
Для доказательства данной формулы достаточно применить интегральное представление для неоднородного уравнения теплопроводности (16) и, учитывая условия (17)–(19), воспользоваться теоремой и оценкой (14).
Эллиптический слой
В области W3 задней критической точки решение строится в переменных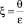 
, 
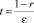, для главного члена получаем следующее уравнение:
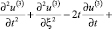
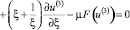, (22)
удовлетворяющее граничным условиям
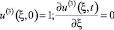при ξ = 0 (23)
и некоторым условиям согласования
u(3)(t, ξ) – u0(t) → 0
при ξ → ∞ в области W∩d. (24)
Функция, определенная равенством u(3)(t, ξ) = u0(t), есть решение задачи (22)–(23), где u0(t) имеет асимптотическое разложение (11) при t > + ∞.
Численное решение
Для решения краевой задачи (9), воспользуемся теоремой о непрерывной зависимости решения от начальных данных и параметров и построенным асимптотическим разложением в теореме. Следует заметить, что постоянная c0,1 – произвольная. Для построения решения краевой задачи уравнение (9) перепишем в виде системы уравнений
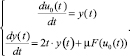(25)
Устойчивость разностных схем проверяем так же, как и в работе [6]. Условие устойчивости явной схемы Рунге – Кутты, будет выполняться, если потребовать выполнения неравенств
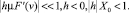(26)
Это значит, что начальное условие следует задать при достаточно большом t0 – и интегрировать назад, т.е. с шагом h < 0. Начальные условия для системы (25) имеют вид
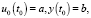(27)
где постоянные a и b определяются из выражения (11).
Рассмотрим случай, когда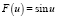 
. Находим последовательные приближения c0n, n = 2, 3, …, для c0.
Далее приводим результаты численных расчётов для уравнения конвективной диффузии на промежутке (0,100):
при m = 0,5, получаем c0,1 = 4,0915, u(0)(0) = 0,9999; y(0) = –1,6507;
при m = 0,8, получаем c0,1 = 8,7293, u(0)(0) = 1,0000; y(0) = –2,6495;
при m = 1, получаем c0,1 = 14,2551, u(0)(0) = 1,0000; y(0) = –3,3221.
Отсюда видим, что решение задачи (9)–(10) функция u(0)(t) удовлетворяет граничному условию в точке t = 0, а при t > + ∞ справедлива оценка O(t-δ).
Заключение
В настоящей работе исследована задача конвективной диффузии внутри сферической капли при больших числах Пекле и малых числах Рейнольдса. Предполагается, что поле скоростей известно. Ранее в работе [4] была исследована задача в случае, когда объёмная химическая реакция носит линейный характер. В нашей работе рассмотрен случай наличия нелинейной объёмной химической реакции. Но при этом главный член разложения в окрестности нуля носит линейный характер. В работе установлено, что в диффузионном пограничном слое d всюду за исключением окрестности задней критической точки порядка O(ε) решение мало отличается (21) в первом приближении от случая линейной химической реакции. Однако в окрестности задней критической точки (в области w3) решение существенно зависит от нелинейной объёмной химической реакции.