Учебная дисциплина «математика» занимает особое место в системе наук, прежде всего она воспитывает критичность мышления и интеллектуальную честность. Однако в последние годы происходит падение мотивации школьников к учебе, в том числе и к изучению математики. Поэтому повышение мотивации учеников к изучению математики это не только актуально, это требование стандарта [1]. Анализ литературы по данной проблеме позволяет сделать вывод, что повысить мотивацию школьников к изучению математики можно путем вовлечения их в проектную деятельность [2–4]. Современная практика показывает, что использование активной проектной деятельности во внеклассной работе по математике позволяет формировать устойчивую мотивацию учащихся к изучению этого предмета [5–7]. Количественной оценке эффективности проектной деятельности посвящена данная работа.
Цель исследования состоит в оценке эффективности проектной деятельности для повышения мотивации школьников к изучению математики. Для достижения этой цели были сформированы две группы школьников, контрольная и экспериментальная. С помощью опросника была измерена мотивация к изучению математики у школьников обеих групп до применения проектного метода обучения. Это необходимо для определения сопоставимости групп по мотивации к изучению математики. Мотивация к изучению математики рассматривается как латентная переменная. Проектный метод обучения использовался только в экспериментальной группе. После проведения эксперимента была измерена мотивация к изучению математики у школьников обеих групп.
Материалы и методы исследования
В исследовании принимали учащиеся 6–7-х классов МБОУ СОШ № 8, Краснодарский край, Калининский район, станица Андреевская, всего 20 школьников.
Измерение уровня мотивации школьников к изучению математики было проведено с использованием теории латентных переменных. Эта теория показала свою эффективность при решении задач в различных социальных системах [8–11]. Для обработки результатов опроса школьников использовалось программно-алгоритмическое обеспечение «Измерение латентных переменных», разработанное в лаборатории объективных измерений Кубанского государственного университете под руководством проф. А.А. Маслака [8].
Результаты исследования и их обсуждение
Оценки мотивации учащихся к изучению математики и индикаторов, которые определяют эту измеряемую латентную переменную, показаны на рис. 1.
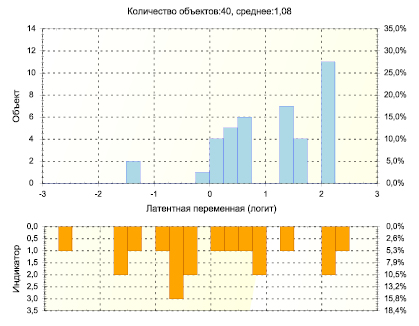
Рис. 1. Оценки учеников и индикаторов на шкале «мотивация к изучению математики»
В верхней части рис. 1 находится гистограмма распределения оценок мотивации учащихся на шкале «мотивация к изучению математики». В нижней части этого рисунка представлены оценки индикаторов на той же шкале.
Результаты измерения, представленных на этом рисунке, позволяют сделать следующие выводы.
1. Оценки мотивации школьников варьируются в диапазоне 3,75 логит (–1,50; +2,25 логит). Это свидетельствует о том, что ученики различаются по уровню их мотивации к изучению математики.
2. Оценки индикаторов варьируются в большем диапазоне – 5,25 логит (–2,75; +2,50 логит). Это свидетельствует о том, что опросник позволяет измерять как высокие, так и низкие уровни мотивации учащихся.
Данные, представленные на рис. 1, свидетельствуют о том, что средняя оценка учеников выше средней оценки индикаторов на 1,087 логит. Таким образом уровень мотивации учеников значительно выше того, на который рассчитан опросник.
В целях иллюстрации рассмотрим один из индикаторов, который лучше других дифференцирует учеников с низкими оценками уровня мотивации к изучению математики.
Таким индикатором является индикатор 13 «Интересным на уроке математики для меня является изучение нового материала с подробным разбором». Зависимость значения этого индикатора от измеряемой латентной переменной «мотивации школьника к изучению математики» представлена в виде характеристической кривой (рис. 2).
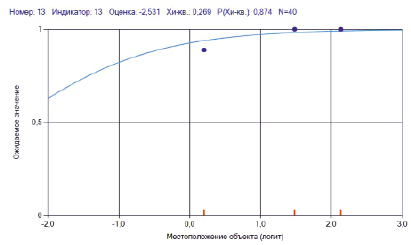
Рис. 2. Характеристическая кривая индикатора 13 «Интересным на уроке математики для меня является изучение нового материала с подробным разбором»
Этот рисунок имеет следующую структуру. На оси абсцисс (в логитах) откладывается значение латентной переменной «Уровень мотивации». Значение индикатора, которое варьируется в диапазоне от 0 до 1, откладывается по оси ординат.
Над рис. 2 находятся показатели, характеризующие этот индикатор:
– 13 – номер индикатора;
– Индикатор 13 – название индикатора по умолчанию;
– –2,531 – оценка индикатора;
– Хи-кв.: 0,269 – статистика Хи-квадрат;
– (P(Хи-кв.): 0,874) – уровень значимости статистики Хи-квадрат;
– 40 – объем выборки.
Оценка индикатора характеризует его местоположение на оси латентной переменной. Низкое значение этого индикатора свидетельствует о том, что наибольшая крутизна характеристической кривой также находится слева. Следовательно, этот индикатор лучше других дифференцирует школьников с низкой мотивацией. Статистика Хи-квадрат и высокий эмпирический уровень значимости этой статистики (0,874) свидетельствует об адекватности этого индикатора модели измерения на номинальном уровне значимости 0,05.
Анализ результатов измерения латентной переменной «мотивация к изучению математики»
В терминах планирования эксперимента откликом Y являются оценки уровня мотивации. Исследовалось влияние на отклик следующих факторов.
Фактор А – пол ученика, фактор варьируется на двух уровнях: девушки и юноши.
Фактор B – время измерения уровня мотивации, фактор варьируется на двух уровнях: до проведения эксперимента, после проведения эксперимента.
Фактор С – использование проектного метода обучения, фактор варьируется на двух уровнях: без использования проектного метода, с использованием проектного метода.
Исследуемые факторы, влияющие на мотивацию школьника – пол ученика, этап измерения, неиспользование/использование проектного метода, являются качественными. Поэтому в качестве метода статистической обработки выбран трехфакторный дисперсионный анализ. Результаты дисперсионного анализа влияния исследуемых факторов представлены в табл. 1.
Таблица 1
Результаты дисперсионного анализа
|
№ п/п |
Источник дисперсии |
Сумма квадратов |
Степень свободы |
Средний квадрат |
Fэксп |
р |
|
1 |
Фактор A |
0,624 |
1 |
0,624 |
1,117 |
0,299 |
|
2 |
Фактор B |
4,178 |
1 |
4,178 |
7,478 |
0,010 |
|
3 |
Фактор C |
1,061 |
1 |
1,061 |
1,900 |
0,178 |
|
4 |
Взаимодействие факторов AB |
0,032 |
1 |
0,032 |
0,058 |
0,811 |
|
5 |
Взаимодействие факторов AC |
0,775 |
1 |
0,775 |
1,388 |
0,247 |
|
6 |
Взаимодействие факторов BC |
5,020 |
1 |
5,020 |
8,986 |
0,005 |
|
7 |
Взаимодействие факторов ABC |
0,073 |
1 |
0,073 |
0,131 |
0,719 |
|
8 |
Ошибка |
17,878 |
32 |
0,559 |
||
|
9 |
Всего |
35,035 |
39 |
Интерпретация результатов дисперсионного анализа. Как следует из табл. 1, значимыми источниками дисперсии являются фактор B, эмпирический уровень которого равен номинальному значению 0,010, и взаимодействие ВС, эмпирический уровень которого равен номинальному значению 0,005.
Тем не менее представляют интерес оценки уровней всех факторов.
В табл. 2 представлены оценки уровней фактора А, который статистически значимо не влияет на уровень мотивации.
Таблица 2
Средние оценки уровня мотивации учащихся в зависимости от пола
|
№ п/п |
Пол ученика |
Среднее (логит) |
Стандартная ошибка (логит) |
95 % доверительный интервал |
|
|
Нижняя граница |
Верхняя граница |
||||
|
1 |
Девушки |
1,008 |
0,212 |
0,576 |
1,439 |
|
2 |
Юноши |
1,301 |
0,179 |
0,936 |
1,665 |
Как видно из табл. 2, также следует, что оценки мотивации к изучению математики (в среднем по всем уровням факторов В и С) у девушек (1,008 логит) меньше, чем юношей (1,301 логит), но, как уже отмечалось, это различие статистически незначимо.
В табл. 3 представлены оценки уровней фактора В. Необходимо отметить, что эти оценки вычислены в среднем для всех уровней А и С, т.е. независимо от пола ученика и использования проектного метода обучения.
Таблица 3
Средние оценки уровня мотивации учащихся в зависимости от этапа, на котором проводится измерение
|
Этап измерения |
Среднее (логит) |
Стандартная ошибка (логит) |
95 % доверительный интервал |
|
|
Нижняя граница |
Верхняя граница |
|||
|
Начальный этап |
0,775 |
0,196 |
0,375 |
1,174 |
|
Конечный этап |
1,533 |
0,196 |
1,134 |
1,933 |
Из табл. 3 видно, что на конечном этапе проведения эксперимента оценка уровня мотивации в среднем для всех уровней А и С (1,533 логит) выше, чем на начальном этапе (0,775 логит). Причем это различие статистически значимо.
В табл. 4 представлены оценки уровней фактора С в среднем для всех уровней факторов А и В.
Таблица 4
Средние оценки уровня мотивации учащихся в зависимости от использования проектного метода обучения
|
Проектный метод |
Среднее (логит) |
Стандартная ошибка (логит) |
95 % доверительный интервал |
|
|
Нижняя граница |
Верхняя граница |
|||
|
Без использования |
0,775 |
0,196 |
0,375 |
1,174 |
|
С использованием |
1,533 |
0,196 |
1,134 |
1,933 |
Фактор С оказался незначимым, прежде всего это обусловлено тем, что оценка эффективности проектного метода проводилась с использованием оценок контрольной группы, где проектный метод не применялся.
Для оценки эффективности проектного метода необходимо рассмотреть оценки эффектов взаимодействия ВС, которое оказалось значимым (табл. 5).
Таблица 5
Эффекты взаимодействия ВС
|
Этап исследования |
Проектный метод |
|
|
Без использования проектного метода |
С использованием проектного метода |
|
|
Начальный этап |
0,999 |
0,550 |
|
Конечный этап |
0,926 |
2,140 |
Для удобства интерпретации эффект взаимодействия представлен на рис. 3.
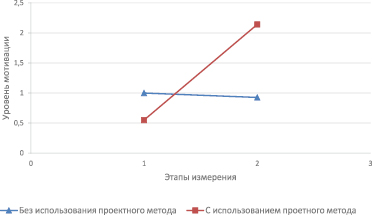
Рис. 3. Эффект проектного метода обучения
Информация, представленная на рис. 3, наглядно свидетельствует об эффективности проектного метода обучения. Так, мотивация контрольной группы (без использования проектного метода) до проведения эксперимента была несколько выше, чем у экспериментальной группы. Однако после проведения эксперимента мотивация к изучению математики статистически значимо увеличилась.
Выводы
1. Полученные в работе результаты свидетельствуют о целесообразности использования теории латентных переменных для измерения «мотивации к изучению математики».
2. Использованный опросник для оценивания уровня мотивации учеников к изучению математики обладает достаточной разрешающей способностью, что позволило оценить эффективность проектного метода обучения.
3. Проектный метод изучения математики значительно повысил мотивацию школьников к изучению математики и рекомендуется для использования в средней школе.
4. Не выявлено статистически значимого различия между юношами и девушками по уровню их мотивации к изучению математики.



