Интенсивность пешеходного движения в городах достаточно велика и оказывает большое влияние на величину задержек автотранспортных средств. Поэтому игнорирование этого факта влечет за собой значительные ошибки в расчетах при выборе оптимального распределения транспортных потоков по улично-дорожной сети. В настоящий период исслледованием влияния пешеходных потоков на загруженность сети занимаются как зарубежные (R.L. Hughes [1], L. Huang, S.C. Wong, M. Zhang [2], M.Di Francesco, P.A. Marcowich [3]), так и отечественные исследователи (Н.А. Скульбеденко, А.Ю. Михайлов [4], Е.Н. Чикалин).
Математические модели транспортных потоков, не учитывающие пешеходное движение, теряют свою привлекательность в силу значительных ошибок при расчете показателей эффективности организации движения на улично-дорожной сети. Актуальной задачей является исследование влияния различных схем организации пешеходного движения на перекрестке на величину задержек транспортных средств. Математическое моделирование этих схем даст возможность выбирать наиболее приемлемую из них в той или иной ситуации.
Цель исследования: разработка методов оценки влияния пешеходных потоков на показатели эффективности функционирования транспортной сети.
Материалы и методы исследования
За адекватность описания транспортного потока и последующую точность расчетов параметров эффективности организации движения отвечает в первую очередь положенная в основу гипотеза о распределении интервалов между транспортными средствами в потоке. В качестве гипотезы о распределении интервалов по времени в каждом из потоков требований в авторской модели TIMeR_Mod [5] принята гипотеза о том, что оно подчинено обобщенному закону Эрланга. Это многопараметрический закон, который позволяет описывать транспортные потоки достаточно высокой плотности. Гипотеза о распределении интервалов по времени между автотранспортными средствами по обобщенному закону Эрланга позволила средствами дифференциального и интегрального исчисления, используя методы теории функций комплексного переменного и теории случайных процессов, вывести в явном виде формулы для вычисления величины задержек в узлах транспортной сети, средней длины очереди у перекрестков, функции транспортных затрат по маршруту сети.
Результаты исследования и их обсуждение
Расчет задержек транспортных средств с учетом пешеходного движения при использовании жесткого режима регулирования и выделения отдельной фазы для пешеходного потока
Рассмотрим случай, когда для пешеходного движения выделена отдельная фаза светофорного цикла в каждом направлении. В модели TIMeR_Mod под задержкой транспортных средств на перекрестке понимается время простоя, тогда как движение в данном направлении запрещено. В этих условиях аналитический аппарат для оценки средней суммарной задержки всех автотранспортных средств на перекрестке аналогичен методу, рассмотренному в работе [6]. Следует только учесть изменения в фазах светофорного цикла.
Введены следующие обозначения:
TgI – время, в течение которого разрешено движение автотранспорта на дороге I (по различным направлениям);
TpI – время, в течение которого разрешено движение пешеходов через дорогу I;
TgII – время, в течение которого разрешено движение автотранспорта на дороге II (по различным направлениям);
TpII – время, в течение которого разрешено движение пешеходов через дорогу II.
–
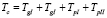длина цикла регулирования; (1)
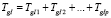, (2)
где TgIi – разрешено движение на дороге I в i-м направлении (тогда в течение времени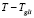 
движение на дороге I в i-м направлении запрещено);
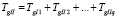, (3)
где TgIIi – разрешено движение на дороге II в j-м направлении (тогда в течение времени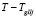 
движение на дороге I в j-м направлении запрещено).
Функция Wi(T, λ) определяет суммарную задержку всех требований потока № i с параметрами обобщенного закона Эрланга, задаваемыми множеством λ, за время T. Подробно аналитическое задание данной функции рассмотрено, например, в работе [6], описан метод вычисления неизвестных коэффициентов функции W(Ti, λ). Для их определения разработана программа в среде DELPHI, получено свидетельство на программу.
В принятых обозначениях средняя суммарная потеря времени всеми транспортными средствами на данном перекрестке за один час равна
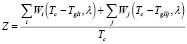. (4)
Условие ликвидации очереди за цикл регулирования по всем направлениям:
, 
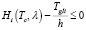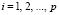; (5)
, 
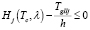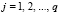. (6)
Здесь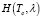 
– функция восстановления, выражает количество автомобилей, прибывающих к перекрестку за время Tc в i-м транспортном потоке с параметрами обобщенного закона Эрланга, задаваемыми множеством λ [6].
Расчет задержек транспортных средств с учетом пешеходного движения при использовании жесткого режима регулирования без выделения отдельной фазы для пешеходного потока
Рассмотрим крестообразный перекресток дорог I и II с жестким светофорным регулированием, но без отдельной фазы для пешеходных потоков. Будем считать, что все участники движения строго соблюдают установленные правила.
Потоки пешеходов, подходящих к перекрестку с целью пересечь дорогу номер i в двух противоположных направлениях, имеют показательное распределение [7] с параметрами λpir и λpil. Их плотности распределения равны соответственно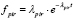 
и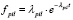 
, где t – время (в секундах) между двумя последовательными появлениями событий (t > 0).
Будем оперировать средними значениями случайных величин, используя свойства их числовых характеристик [8]. Среднее количество пешеходов, подошедших к перекрестку за время, в течение которого разрешено его пересечение в данном направлении, равно:
– для дороги I в двух противоположных направлениях движения пешеходов
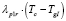(7)
и
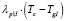; (8)
– для дороги II в двух противоположных направлениях движения пешеходов
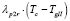(9)
и
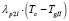. (10)
Тогда среднее время, необходимое автотранспорту для пропуска пешеходов, следующее:
– для дороги I
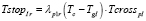(11)
и
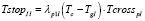; (12)
– для дороги II
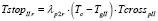(13)
и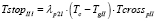 
. (14)
Здесь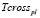 
и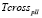 
– среднее время, необходимое пешеходу для пересечения дороги I и II соответственно.
Учитывая необходимость пересечь перекресток группе пешеходов, подошедших за время запрещающего сигнала светофора, получим следующее среднее время простоя:
– для дороги I:
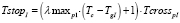, (15)
где
;
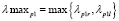– для дороги II:
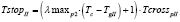, (16)
где
.
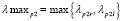С учетом вышесказанного средняя суммарная часовая задержка всех транспортных средств на данном перекрестке равна
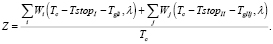(17)
Описанный в данном пункте режим регулирования целесообразен при следующих условиях:
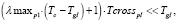(18)
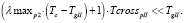(19)
В противном случае в данной узловой точке транспортной сети образуется затор.
Расчет задержек транспортных средств с учетом пешеходного движения при использовании вызывных устройств
Движение пешеходов в течение суток неравномерно. Пиковые периоды часто набюдаются в утренние и вечерние часы. И применение жесткого светофорного регулирования влечет к неоправданно высоким задержкам автомобильного транспорта.
В Великобритании широко применяются пешеходные переходы с вызывными устройствами (PUFFIN и Pelican). Такая технология позволяет оптимизировать потери времени как автотранспорта, так и пешеходов.
Рассмотрим крестообразный перекресток дорог I и II, на котором имеется только вызывное устройство для пропуска пешеходов на главной дороге. Без ограничения общности можно считать, что I – главная дорога, II – второстепенная.
В этом случае средняя задержка автотранспортных средств зависит от случайного процесса прибытия пешеходов к данному переходу. Введем следующие обозначения:
tw – время ожидания включения зеленого сигнала для пешеходов после нажатия кнопки вызова, с;
tgpI – длительность разрешающего сигнала для пешеходов, пересекающих дорогу I, с;
tover – длительность промежуточного такта для освобождения проезжей части от пешеходов, с;
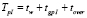– длительность горения разрешающего сигнала для пешеходов, пересекающих дорогу I, с;
tga – минимальная длительность разрешающего сигнала для автотранспортных средств, с.
Автомобили главной дороги I должны пропустить только пешеходов. Прибытие автомобилей дороги I к перекрестку никак не зависит от прибытия пешеходов к нему, поэтому средняя часовая задержка одного автомобиля, совершающего движение по главной дороге, может быть оценена следующим образом:
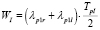. (20)
Рассмотрим задержки автотранспортных средств второстепенной дороги II. Так как на ней нет вызывного устройства для пешеходов, то можно повторить доказательство теоретического положения 2.3 из работы автора [6], добавив к пересекаемым потокам два противоположно напарвленных пешеходных потока. Временные интервалы в транспортных потоках главного направления распределены по обобщенному закону Эрланга с параметрами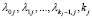 
– параметры обобщенного закона Эрланга для j-го пересекаемого потока (
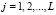) соответственно, а в пешеходных – с параметрами λpir и λpil (показательный закон распределене является частным случаем обобщенного закона Эрланга при k = 1). Т0 – приемлемый для продолжения движения интервал (в секундах).
Для автомобилей второстепенной дороги II среднее время ожидания (в секундах) возможности пересечь L транспортных потоков главной дороги и пропустить потоки пешеходов, переходящих дорогу II, равно
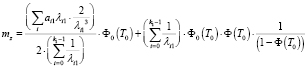, (21)
где
,
.
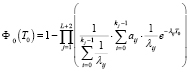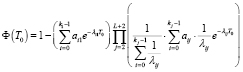Тогда средняя задержка (в секундах) у нерегулируемого перекрестка одного требования данного второстепенного направления с учетом очереди равна
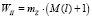, (22)
где
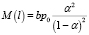, (23)
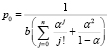, (24)
, 
, 
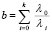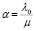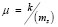. (25)
Средняя суммарная часовая задержка всех транспортных средств на перекрестке с вызывным устройством для пешеходов следующая:
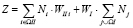, (26)
где Ni, Nj – интенсивности (кол/час) транспортных и пешеходных потоков по всем направлениям движения,
ΩI – множество всех направлений дороги I,
ΩII – множество всех направлений дороги II.
Заключение
Изложенные в работе методы расчета задержек автотранспортных средств с учетом пешеходного движения выполнены в рамках гипотез и установок авторской модели TIMeR_Mod распределения транспортных потоков по сети, которая нацелена на решение оптимизационных транспортных задач в режиме oнлайн. Учет пешеходных потоков позволит более точно моделировать реальную дорожную ситуацию и оперативно реагировать на ее изменения.