Выпускники, подготовленные по информационным технологиям, устраиваются на работу в организации, где применяется компьютерная информация, находящаяся в файлах, в базе данных или поступающая от каких-либо устройств. В этих организациях может производиться автоматизированная обработка информации. Обрабатываться данные могут различными алгоритмами, которые нередко приходится реализовывать на языках программирования. От некоторых вышеуказанных выпускников работодатели будут требовать соответствующих знаний, умений и навыков (ЗУН). Формирование таких ЗУН производится при изучении различных дисциплин учебных планов. Методика их изучения предполагает компетентностный подход [1].
Работодатели в дополнение к образовательным стандартам могут выдвигать свои требования (профессиональные запросы [2]), для удовлетворения которых нужны дополнительные компетенции. Требуемые работодателем умения разноплановы, таким образом, подготовка студентов представляет собой процесс, имеющий набор входных воздействий и набор выходных значений. В данной работе из выходных значений ограничимся рассмотрением только компетенций по обработке информации, находящейся в файловой системе.
Цель работы: формализация процесса формирования у студентов компетенций по обработке информации, находящейся в персональном компьютере, с помощью математического аппарата.
Решаемые задачи:
– формулирование требований к ЗУН студентов, связанным с обработкой данных в персональном компьютере;
– представление процесса обучения этим ЗУН с помощью математической модели;
– вывод аналитических формул и автоматизация вычислений по этим формулам.
Формулировка требований
Для разработки программ по обработке данных требуются две компетенции: Z1 и Z2 (соответственно «Параллельная обработка файлов и каталогов» и «Обработка баз данных и таблиц»). Проведен анализ текстов компетенций различных образовательных стандартов [3], и для примера выбраны бакалавры, обучаемые по направлению 09.03.03 «Прикладная информатика». Для выполнения требований рассматриваемых компетенций студенты обучаются дисциплинам, представленным в табл. 1, где приводятся также обозначения формируемых ЗУН.
ЗУН логически объединяются в группы (табл. 2).
Таблица 1
Дисциплины, формирующие ЗУН
|
Дисциплина или группа дисциплин |
ЗУН (см. табл. 2) |
|
P1 – Информатика и программирование, Основы программирования, Программирование на языке высокого уровня |
g11, g12, g21, g84 |
|
P2 – Объектно-ориентированное программирование |
G1 |
|
P3 – Интернет-технологии |
g83 |
|
P4 – Алгоритмы и структуры обработки данных |
g12 |
|
P5 – Основы баз данных, СУБД |
G6, g32, g53, g55, g82, g83, g51 |
|
P6 – Операционные системы и сети |
G2, G3, G4, G5, g73 |
|
P7 – Локальные, корпоративные и глобальные информационные сети |
g31, g32, G7 |
|
P8 – Иностранный язык, Русский язык и основы креативного письма |
g81 |
Таблица 2
Группы ЗУН и их состав
|
Группа ЗУН |
ЗУН (при разработках в Delphi) |
|
G1 – Базовые навыки программирования |
g11 = {Циклы, условия, подпрограммы, рекурсии, обработка строк, типы данных, выбор варианта, операторы, массивы, среда разработки} |
|
g12 = {Теория алгоритмов} |
|
|
g13 = {Классы} |
|
|
G2 – Файловые примитивы и функции |
g21 = {Read, Write, EOF, Reset, Rewrite, Append, Close, Closefile} |
|
g22 = {Seek, BlockRead, BlockWrite} |
|
|
G3 – Операции и диалоги над каталогами и файлами |
g31 = {ChDir, GetCurrentDir, MkDir, DirectoryExists, CreateDir, SelectDirectory} |
|
g32 = {TOpenDialog(Execute, FileName, Filter), TSaveDialog} |
|
|
g33 = {FileExists, FindFirst, FindNext, FindClose} |
|
|
G4 – Функции для работы с файловыми атрибутами |
g41 = {ExtractFileName, Name, Size, ExtractFileExt, Time, Attr} |
|
G5 – Визуальные элементы и диалоги |
g51 = {Showmessage, TPanel, TEdit, TRichEdit, TMemo} |
|
g52 = {TMainMenu, TListView(Items, SubItems, CheckBoxes), InputBox, TListBox} |
|
|
g53 = {TSplitter} |
|
|
g54 = {TButton} |
|
|
g55 = {TCheckBox} |
|
|
G6 – Базы данных и таблицы |
g61 = {Реляционные СУБД, визуальные элементы для работы с данными, интерфейс прямого доступа, разрешение конфликтов, ключи, связи между таблицами, SQL, диаграммы, GUI-объекты} |
|
Окончание табл. 2 |
|
|
Группа ЗУН |
ЗУН (при разработках в Delphi) |
|
G7 – Распараллеливание в сети |
g71 = {Методы модуля Winsock(SendTo, Recv, Bind, Socket, Listen)} |
|
g72 = {TTCPClient, TTCPServer} |
|
|
g73 = {Создание потоков (интерфейс класса TThread)} |
|
|
G8 – Общие вопросы |
g81 = {Владение русским и английским языками} |
|
g82 = {ShellExecute} |
|
|
g83 = {HTML} |
|
|
g84 = {пользование ПК} |
|
Математическая модель
Для формализации предлагается использовать сети Петри – математический аппарат, позволяющий наглядно представлять причинно-следственные отношения, в том числе в учебном процессе [4]. Предлагается следующая модель на основе сети Петри (рисунок).
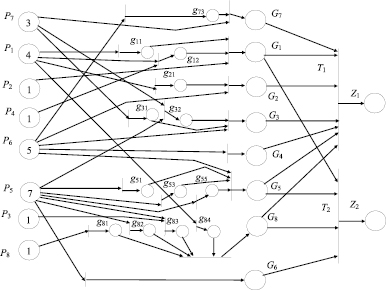
Модель на основе сети Петри
В данной модели числа в позициях P1 – P8 означают количество маркеров при начальной маркировке; эти позиции представляют одноименные дисциплины (табл. 1). Позиции Z1 и Z2 моделируют получение одноименных компетенций. Позиции gij моделируют одноименные ЗУН, при этом некоторые ЗУН не имеют позиций с такими названиями, так как дисциплина может обеспечивать знаниями группу ЗУН целиком. Позиции G1 – G8 представляют одноименные группы ЗУН. Срабатывание переходов непосредственно слева от этих позиций означает приобретение ЗУН и их групп в итоге обучения. Переходы T1 и T2 формируют компетенции из групп ЗУН.
Группы ЗУН иногда формируются как результат изучения в другом ракурсе уже пройденных тем при изучении разных дисциплин, что представлено более чем одной входящей дугой в соответствующий переход. То же касается отдельных ЗУН.
Сеть Петри является раскрашенной, так как маркеры имеют атрибуты. Чтобы не извлекать лишние маркеры, переходы при срабатывании извлекают только те маркеры, значение атрибутов которых равно названию выходной позиции (компетенции). Значения атрибутов маркеров в позициях P1 – P8 соответствуют содержимому столбца «ЗУН» (табл. 1).
ЗУН подвержены забыванию, в связи с чем каждому маркеру присвоен еще один атрибут – уровень остаточных знаний, обозначаемый c [2], который можно выразить числом в диапазоне от 0 до 1. Тогда даже если для некоторого маркера cij = 0, переход всё равно будет срабатывать, т.е. модель работоспособна, несмотря на отсутствие знаний, где i – номер группы ЗУН, j – номер ЗУН внутри группы.
Модель упрощена по сравнению с [2], так как моделирует только необходимые компетенции и факт наличия дисциплины, а не распределение по семестрам и последовательность дисциплин. Это позволяет сделать модель более компактной. Таким образом, она учитывает cij только в конце обучения, после защиты выпускной работы, опираясь на полученные каким-то образом оценки итоговых остаточных знаний.
После определения этих оценок важно оценивать компетенции выпускника для работодателя, что является актуальным вопросом [5]. Для этого в простейшем случае можно вычислить среднее значение cij по всем ЗУН, нужным для данной компетенции, однако этот подход имеет следующий недостаток. Если студент что-то выучил на «отлично», а что-то совсем не знает, в среднем определяется удовлетворительный уровень. Но одному работодателю нужны одни знания, другому – другие, и не ясно, которому из них удовлетворяют знания выпускника. Поэтому атрибут c как для Z1, так и для Z2 предлагается представлять не скалярным значением, а множеством X = {X1, X2, …X8}, наподобие выписки из зачетной ведомости, где по каждой дисциплине проставляется своя оценка.
Например, студент может не знать параллельную обработку (X7 = 0), но обладает базовыми навыками программирования: X1 = 1. Параллельная обработка не всегда нужна, и выпускник сможет удовлетворить требования некоторых работодателей. Нужно отметить, что если какие-то ЗУН не изучались в одной дисциплине, то они могли изучаться в другой, поэтому X = {Xi} = max{cij}, где cij находится в изъятых маркерах, i = 1,…,8, j принимает значения в диапазонах, соответствующим количеству подгрупп в группах ЗУН.
Разные ЗУН на практике востребованы по-разному. Поэтому предлагается ввести весовые коэффициенты отдельных ЗУН по средней востребованности работодателями, которые являются экспертными оценками. Экспертные оценки коэффициентов востребованности ЗУН обозначим kij, а их средние значения по группам ЗУН – Ki,ср, где i, j имеют тот же смысл, что и для cij.
Возможно создание интегральных скалярных оценок по компетенциям Z1 и Z2. Один из способов – использование вероятностных интегральных оценок компетенций, учитывающих вероятность того, что выпускнику придётся столкнуться с той или иной задачей. Выражение представляет собой произведение
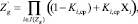
где I(Zg) – индексы групп ЗУН, формирующих g-ю компетенцию, g принимает значение 1 или 2.
Если при этом учитывается множество групп ЗУН, в итоге образуется ничтожная величина, так как знания по каждой группе в основном значительно менее 1. В связи с этим необходимо укрупнять группы умений, что является более сложной задачей, требующей высокой квалификации от лиц, занимающихся оцениванием.
Поэтому уровни знаний по группам ЗУН предлагается определять по формуле
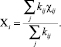 (*)
(*)
Формулу (*) с некоторыми изменениями применим для оценки Z1 и Z2:
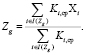
Методики оценивания ЗУН, такие как тесты, дают приблизительную оценку, что связано с надёжностью тестов [6], таким образом, предлагаемый набор может быть представлен в виде набора диапазонов. Предлагается для определения этих диапазонов применять нечеткие множества [7]. Для примера используем следующие значения. Пусть k11 = 1 (так как точно известно, что g11 требуется на любой работе по специальности), k12 = (0,3÷0,7), k13 = (0,8÷1); c11 = (0,5÷0,9), c12 = (0,1÷0,3), c13 = (0,3÷ 0,7), тогда согласно формуле (*):
X1 = [(0,5÷0,9)•1 + (0,1÷0,3)•(0,3÷0,7) + + (0,2÷0,4)•(0,8÷1)]/[1 + (0,3÷0,7) + (0,8÷1)].
Примем, что нечеткие множества, задаваемые указанными интервалами, изображаются на графике функции принадлежности в виде треугольников, где крайние значения интервалов имеют значение функции принадлежности 0,5, а средние значения интервалов – соответственно 1. Таким образом, все применяемые нечеткие множества выпуклые. Переходя к обозначениям нечетких множеств, и учитывая специфическое использование в них символов деления и сложения, получаем
k~12 = {0,3/0,5 + 0,5/1 + 0,7/0,5},
k~13 = {0,8/0,5 + 0,9/1 + 1/0,5},
c~11 = {0,5/0,5 + 0,7/1 + 0,9/0,5},
c~12 = {0,1/0,5 + 0,2/1 + 0,3/0,5},
c~13 = {0,3/0,5 + 0,5/1 + 0,7/0,5}.
В формуле (*) задействуются операции сложения, умножения и деления нечетких множеств. При выполнении каждой из этих операций «знаменатели» нечетких множеств поэлементно умножаются. Что касается «числителей», то они поэлементно при умножении умножаются, при сложении суммируются, а при делении делятся друг на друга. При этом отбрасываются элементы, для которых значения функции принадлежности, т.е. «знаменатели» элементов нечетких множеств, после выполнения арифметической операции менее 0,5, а ко всем элементам с одинаковым значением функции принадлежности применяются операции min и max с целью охвата наибольшего интервала универсального множества.
Для автоматизации таких вычислений разработана таблица с формулами в Microsoft Excel, позволяющая вычислять Z1 или Z2 на основе нечетких множеств, причем максимальное количество групп ЗУН равно восьми, число ЗУН в группе не более пяти.
Используя разработанную таблицу, получено
k~12•c~12 = {0,3/0,5 + 0,5/1 + 0,7/0,5}•{0,1/0,5 + + 0,2/1 + 0,3/0,5} = = {0,05/0,5 + 0,1/1 + 0,15/0,5},
что соответствует диапазону 0,05÷0,15. Аналогично получено
k~13•c~13 = {0,16/0,5 + 0,27/1 + 0,4/0,5}.
Подставляя значения в таблицу Microsoft Excel, получено значение для первой суммы в числителе X1:
{0,5/0,5 + 0,7/1 + 0,9/0,5} + {0,05/0,5 + + 0,1/1 + 0,15/0,5} = {0,6/0,5 + 0,8/1 + 1/0,5}.
Складывая полученное выражение с k~13•c~13, получено значение для числителя X1:
{0,6/0,5 + 0,8/1 + 1/0,5} + {0,16/0,5 + 0,27/1 + 0,4/0,5} = {0,87/0,5+1,07/1 + 1,27/0,5}.
Вычисленный аналогичным образом знаменатель следующий:
{2,2/0,5+2,4/1+2,6/0,5}.
Используя разработанную таблицу Excel, получено
X1 = {0,87/0,5+1,07/1 + 1,27/0,5}: :{2,2/0,5+2,4/1+2,6/0,5} = = {0,3625/0,5 + 0.4458/1 + 0,5292/0,5}.
Соответствующий диапазон составляет
X1 ≈ 0,4458÷0,0833.
Таким образом, предлагаемая методика оценивания готовности выпускника к работе включает в себя распределение требуемых компетенцией ЗУН по дисциплинам с возможным дублированием (общее для всех студентов группы), оценку востребованности ЗУН среди работодателей, оценивание ЗУН конкретного студента по темам и вычисление множества интегральных оценок студента с применением нечетких множеств.
Заключение
Выпускники решают и другие задачи по информационным технологиям, готовность к которым можно выражать компетенциями, дополняющими стандарты. Например, часто требуется также умение создания сайтов, системного администрирования и др. Эти компетенции также можно оценивать по предлагаемой методике. Оценив определённые знания конкретного студента с помощью каких-либо методик, далее можно получить число, характеризующее некоторую компетенцию. Применяемая для выполнения требуемых операций над нечеткими множествами таблица Microsoft Excel содержит 89 строк, 14 столбцов и 429 формул. Анализ предложенной сети Петри показывает, что не имеется бесконечного накопления маркеров. Каждый переход срабатывает только один раз.



