Эффективная эксплуатация систем защиты информации (СЗИ) корпоративных сетей передачи данных (КСПД), их проектирование и модернизация невозможны без оценки характеристик процесса по обнаружению вредоносных воздействий, процесса восстановления зараженных узлов сети и планирования работ по профилактике заражения. Проблема защиты цифровой информации от вредоносных программ (ВП), таких как компьютерные вирусы, шпионские и троянские программы, сетевые черви, программы-шантажисты и др., является актуальной и значимой в настоящее время [1, 2] несмотря на то, что первый известный вирус был написан в далеком 1981 г., а современный рынок информационных технологий предлагает множество решений по антивирусной защите. Но ни одна система защиты информации не способна блокировать проникновение вредоносного программного обеспечения (ПО) в корпоративную сеть на 100 %. Современная СЗИ, включающая систему обнаружения и предотвращения атак и вторжений IPS/IDS, не может гарантировать обнаружения 70 % информационных атак, что периодически приводит к значительному возрастанию вредоносного трафика (ВТ) [3, 4].

По данным компании Positive Technologies [5] самым распространенным методом атак стало использование вредоносного программного обеспечения: в I квартале 2018 г. вредоносное ПО применялось в 63 % уникальных кибератак (+27 % по сравнению с аналогичным периодом 2017 г. [6]). Большую популярность получила троянская программа WannaMine, заразившая по всему миру более 500 000 устройств.

Цель исследования: разработать математическую модель процесса устранения вредоносных воздействий, использование которой обеспечит возможность оценки качества работы СЗИ и функционирования КСПД в различные моменты времени в зависимости от начального числа вредоносных воздействий (вредоносных программ), используемых методов обнаружения и противодействия.

Под вредоносным воздействием будем понимать распространение вредоносных программ в КСПД, любые их действия, которые могут привести к нарушению работоспособности как отдельных узлов, так и сети в целом.

Математическая модель. Для моделирования процесса устранения вредоносных воздействий в узлах КСПД возьмем за основу математическую модель процесса отладки программного обеспечения, предложенную в книге [7] исследователями А.Г. Мамиконовым, В.В. Кульба, А.Б. Шелковым и получившую дальнейшее развитие в диссертации А.И. Крапчатова [8].

Пусть КСПД состоит из множества узлов (компьютерных систем, КС – S), в каждом из которых протекает марковский процесс [9, 10] по устранению вредоносных воздействий. Система S может находиться в одном из дискретных состояний: s0, s1,…, sN, где N – количество вредоносных воздействий (как частный случай, N может быть равно числу вредоносных программ в узле сети), а s0 – поглощающее состояние, означающее, что все вредоносные воздействия устранены и процесс сканирования узла окончен.

Под устранением вредоносного воздействия (или вредоносной программы) в узле сети будем понимать его обнаружение и моментальное восстановление КС. Интенсивность устранения вредоносных воздействий будем считать пропорциональным их количеству.

Определим результативность сканирования системы S величиной pij – вероятностью того, что после сканирования в КС, содержащей i 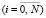вредоносных воздействий, останутся необнаруженными j (j ≥ i или j < i), 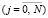, где N – количество вредоносных воздействий до начала сканирования. Зададим распределение pij в виде матрицы:

(1)

Модель базируется на предположении, что после устранения вредоносного воздействия (вредоносной программы) в узле сети появиться вновь оно уже не может, то есть КС приобретает к нему иммунитет. Система может иметь несколько поглощающих состояний, означающих, что процесс сканирования может быть остановлен, но не все вредоносные воздействия устранены.

Методы и средства исследований. Анализ предложенной модели позволил сделать вывод, что наиболее важными характеристиками процесса устранения вредоносных воздействий в условиях ограниченности времени (ресурсов) являются [7, 8]:

1) математическое ожидание (МО) времени устранения j вредоносных воздействий (j ≥ i или j < i), :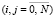

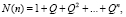
где n – количество циклов обнаружения вредоносных воздействий;

2) МО времени устранения всех вредоносных воздействий в компьютерной системе:

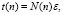
где ε – единичный вектор-столбец;

3) вероятность устранения всех вредоносных воздействий в компьютерной системе:

;

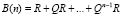4) МО времени, в течение которого в компьютерной системе существует постоянное число вредоносных воздействий:

;

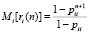5) вероятность того, что в компьютерной системе находится j вредоносных воздействий:

,

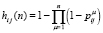где 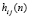– элементы матрицы H(n).

При последовательном устранении вредоносных воздействий (или вредоносных программ) в узлах компьютерной сети в режиме неограниченного времени можно определить следующие наиболее важные характеристики трудоемкости процесса [7, 8]:

1) МО времени устранения всех вредоносных воздействий в компьютерной системе:

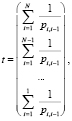
где 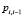– вероятность того, что после одного сканирования в КС будет i – 1 вредоносных воздействий;

2) дисперсия времени устранения всех вредоносных воздействий в компьютерной системе:

;

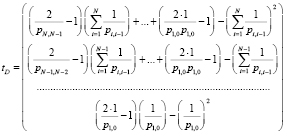3) вероятность устранения всех вредоносных воздействий в компьютерной системе:

,

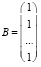то вероятность устранения всех вредоносных воздействий стремится к единице;

4) МО времени, в течение которого в компьютерной системе существует постоянное число вредоносных воздействий:

;

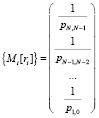5) дисперсия времени, в течение которого в компьютерной системе существует постоянное число вредоносных воздействий:

;

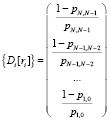6) вероятность того, что в КС находится j вредоносных воздействий:

.

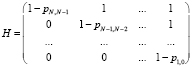На основе представленной математической модели процесса устранения вредоносных воздействий в узлах компьютерной сети можно получить характеристики процесса распространения вредоносных программ.

Рассмотрим компьютерную сеть передачи данных как сеть массового обслуживания [11, 12], в которой циркулируют пакеты в соответствии с маршрутной матрицей 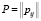, где pij – вероятность пересылки пакета из i-го в j-й узел, причем 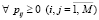и .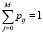

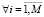Пусть в качестве пакета в КСПД попадает вредоносная программа, тогда в сети будет протекать случайный процесс распространения ВП. Сеть может находиться в одном из дискретных состояний: 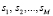, где 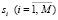означает, что ВП находится в i-м узле.

Важными с практической точки зрения являются следующие вопросы:

1. Сколько шагов будет совершено до остановки процесса распространения ВП, то есть поглощения в том или ином состоянии?

2. Каково время распространения вредоносной программы в сети?

3. Какой узел будет заражен раньше остальных?

Продемонстрируем ответы на поставленные вопросы на примере сети, состоящей из пяти узлов, пакеты в которой пересылаются в соответствии с матрицей:

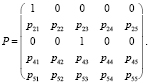(2)

С помощью преобразований приведем матрицу (1) к блочной форме:

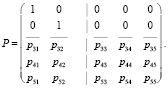(3)

На основании (3) получена матрица, называемая фундаментальной:

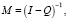(4)

где I – единичная матрица;

Q – квадратная подматрица переходов:

.

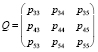Каждый элемент матрицы (4) соответствует среднему числу раз попадания системы в то или иное состояние до остановки процесса распространения ВП. Умножение справа матрицы M на единичный вектор e позволяет получить общее среднее количество раз попадания системы в то или иное состояние до поглощения:

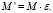
Зная время пребывания системы в каждом состоянии, можно вычислить общее время до поглощения :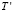

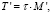
где вектор t – время пребывания системы в каждом невозвратном состоянии.

Матрица (2) описывает переходы сети, имеющей два поглощающих состояния. Обозначим через bij вероятность того, что процесс завершится в некотором поглощающем состоянии sj при условии, что начальным было состояние si 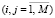. Вероятности bij образуют матрицу B, строки которой соответствуют невозвратным состояниям, а столбцы – всем поглощающим состояниям:

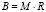, (5)

где .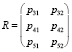

Анализ матрицы (5) позволяет оценить и сравнить вероятности заражения восприимчивых узлов и при построении защиты обезопасить наиболее уязвимые.

Для наглядности произведем вычисления для системы, переходы в которой заданы следующей матрицей:

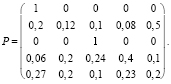
По формуле (5) получим матрицу:

Таким образом, если процесс распространения ВП начался из третьего узла сети, то вероятность заражения первого узла равна 0,608, а второго – 0,392.

Для оценки характеристик процесса устранения вредоносных воздействий в КСПД разработана математическая модель, базирующаяся на теории сетей массового обслуживания. На основе предложенной модели возможна не только оценка характеристик процесса устранения вредоносных воздействий, но и процесса распространения ВП в сети. Применение модели наиболее целесообразно для определения вероятности и времени тотального инфицирования корпоративной сети. Предсказание данных характеристик информационных атак, реализуемых с помощью вредоносного программного обеспечения, и трудоемкости по устранению вредоносных воздействий позволит более эффективно использовать средства противодействия и уменьшать последствия данных воздействий.