Одним из направлений совершенствования современных производственных технологий является создание процессов выполнения гибридных операций одним техническим устройством [1]. При обработке роботами крупных объектов потребуется выполнять разнотипные операции, такие как очистка поверхности, резка, сварка, механическая обработка или обработка направленным потоком энергии, например лазерным лучом.
Роботы могут являться основным рабочим инструментом при гибридной обработке крупногабаритных объектов (резервуаров, корпусов судов, гребных винтов больших размеров и т.д.), включающей очистку поверхности, сварку и механическую обработку при ремонте или изготовлении с использованием концентрированных потоков энергии сжатой жидкости или лазерного излучения.
Цель работы – решение ряда вопросов построения исполнительной системы, предназначенной для работы с объектами больших габаритов.
На рис. 1 приведены обобщенные манипуляционные функции, реализуемые в рассматриваемой манипуляционной системе в зависимости от выполняемых операций и реализуемых перемещений.
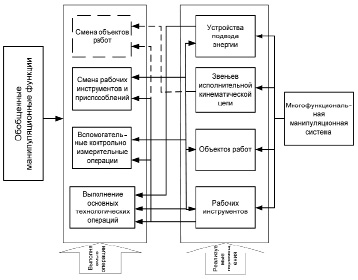
Рис. 1. Обобщенные манипуляционные функции, реализуемые в манипуляционной системе
Из анализа обобщенных манипуляционных функций, реализуемых в манипуляционной системе, следует, что она должна представлять собой совокупность исполнительных устройств (манипуляторов), параметры которых должны определяться функциональным и кинематическим комплексированием, последовательность которого приведена на рис. 2.
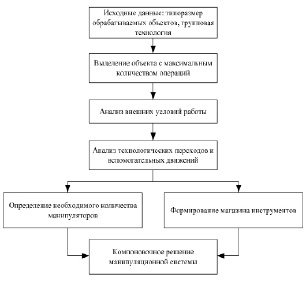
Рис. 2. Последовательность комплексирования манипуляционной системы
При этом система должна удовлетворять требованиям, основными из которых являются:
– оптимальное число манипуляторов;
– минимум величины потребляемой энергии;
– обеспечение необходимой точности при значительной длине звеньев;
– возможность обработки объектов в условиях неопределенности их геометрической формы и положения;
– выполнение комплексных технологических операций с одной позиции;
– транспортабельность.
На рис. 3 представлена структурная схема манипуляционной исполнительной системы робота, отражающая ее состав.
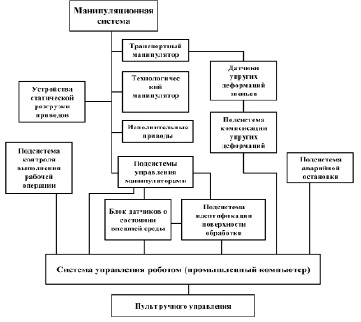
Рис. 3. Структурная схема манипуляционной исполнительной системы робота
Предлагается манипуляционную исполнительную систему робота выполнять в виде последовательно соединенных координатного манипулятора (м1) и производственного (м2). М1 может осуществлять перестановку М2 с фиксацией на объекте отработки или может выполнять рабочие операции совместно с М1. Общая длина манипуляторов может быть более 10 м.
На рис. 4 приведена кинематическая структура предлагаемой манипуляционной исполнительной системы. Здесь обозначены φi – вращательные степени подвижности, а Si – поступательные степени подвижности. Транспортный манипулятор имеет 3 степени подвижности, необходимых и достаточных для перемещения технологического манипулятора в заданную точку рабочей зоны, а технологический манипулятор обладает 6 степенями подвижности для обеспечения необходимой маневренности при выполнении разнообразных операций. Структурный синтез такой системы может быть выполнен по методике, изложенной в работе [2].
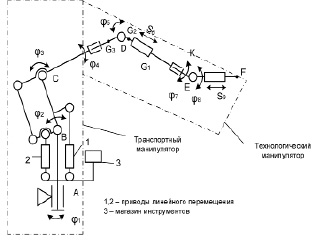
Рис. 4. Кинематическая структура манипуляционной исполнительной системы для обработки крупногабаритных объектов
При большой длине предлагаемой кинематической цепи на приводы будут действовать значительные статические нагрузки и проявляться сильное взаимовлияние звеньев. Поэтому манипуляционную систему необходимо оснастить устройствами статической разгрузки приводов с возможностью уменьшения взаимовлияния звеньев. В робототехнике статическая разгрузка, описанная в работе [3], осуществляется с использованием систем специальных механических устройств или устройств, использующих сжатую рабочую среду (воздух или жидкость).
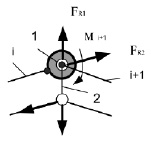
Рис. 5. Схема моментной разгрузки приводов
В предлагаемой манипуляционной системе разгрузку приводов вращательных степеней подвижности целесообразно осуществлять по схеме, приведенной на рис. 5. Здесь момент нагрузки Mi+1, действующей на привод перемещения i + 1-го звена с помощью дополнительных удерживающих связей, образующих параллелограммные механизмы, раскладываются на составляющие усилия FR1 и FR2. Усилия FR1 воспринимаются стержнем 2 и взаимно компенсируются, а усилия FR2 действуют вдоль стержней звена i без образования реактивного момента. Привод 1 должен быть снабжен синусно-косинусным механизмом статической разгрузки, предложенном в патенте [4].
Точность работы системы манипуляторов М1 и М2 во многом зависит от жесткости механической системы, которая определяет величины деформации от действия статических и динамических нагрузок. Поэтому необходима подсистема компенсации упругих деформаций. Если собственная статическая деформация М1 может быть скомпенсирована программно, то влияние параметров движения М2 требует введения дополнительной коррекции. Считая, что звенья М2 являются жесткими положение рабочей точки инструмента (т. С) в инерциальной системе отсчета, располагаемой на основании М1 в точке О, без учета податливости манипулятора М1 можно определить с помощью однородных матриц, предлагаемых в работе [5]:
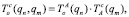(1)
где А – точка соединения М1 и М2;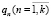 
, 
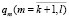– обобщенные координаты М1 и М2. С учетом пространственной ориентации рабочего инструмента зависимость (5) можно записать в виде
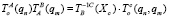, (2)
где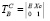 
; Хс – вектор направления рабочего инструмента. В случае деформируемого М1 выражение (6) можно свести к виду
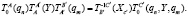(3)
Здесь Y – вектор размером 6×1 линейных и угловых деформаций М1 для точки А,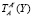 
– матрица координатных преобразований. Анализ выражений (6) и (7) показывает, что для определения величин компенсации деформаций кинематических цепей М1 и М2 следует решать обратную задачу для точек в координатах манипулятора М2 из матричных зависимостей для приращений координат Δqm
(4)
В то же время определение указанных выше приращений Δqm по выражению (8) при невырожденной матрице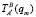 
следует считать нерациональным из-за сложной процедуры вычисления параметров Y. Более эффективно решать поставленную задачу, учитывая силомоментное взаимодействие между М1 и М2. Тогда можно воспользоваться зависимостью
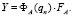(5)
Здесь ФА(qn) матрица обратной податливости М1 для точки А; FA – вектор сил и моментов взаимодействия М1 и М2 размером 6×1.
Величины, входящие в матрицу ФА(qn), можно найти для произвольных положений манипулятора М1 с использованием уравнений статики рекурентно, а параметры FA можно измерить с помощью датчиков или вычислить как реактивные составляющие в процессе движения манипулятора М2. Определение параметров вектора FA путем измерения многокомпонентным датчиком с необходимой фильтрацией обладает большим быстродействием и точностью. Ввиду нелинейного характера определения Δqm и положительности компенсирующей связи в системе возможно возникновение низкочастотных периодических режимов, что требует соответствующей коррекции. Если лазер-робот является универсальным, то М2 может обладать сменным инструментом и выполнять операции при наложенных связях и силовых воздействиях. При действии обобщенной силы Fc в рабочем инструменте и позиционном управлении необходимые моменты в сочленениях М2 с учетом компенсации деформаций определяются выражением
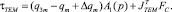(6)
Назначение и структура остальных подсистем, приведенных на рис. 3, очевидны.
Выводы
1. Предложена структура и кинематическая схема манипуляционной исполнительной системы робота для обработки крупногабаритных объектов, включающая два последовательно соединенных манипулятора.
2. Для уменьшения взаимовлияния звеньев и нагрузок на приводы предложена схема моментной разгрузки.
3. Предложено решение задачи компенсации упругих деформаций звеньев на основе вычисления матриц податливости или измерения вектора взаимодействия между манипуляторами.