Одной из задач вычислительных систем, как совокупности аппаратно-программных средств, образующих единую среду, предназначенную для решения задач обработки информации, является обнаружение, различение или распознавание образов [1, 2]. Актуальным вопросом является синтез оптимальных устройств распознавания образов или сигналов. Такие устройства должны обладать максимальной производительностью, что может быть обеспечено только на основе параллельной технической базы, такой как нейронные сети (НС). Одним из основных достоинств НС является возможность их к самообучению [3, 4]. Самообучение сводится к адаптации весовых коэффициентов wij сети или обратных синоптических i-х связей j-го нейронного слоя. То есть НС способна к адаптации к реальным условиям. В реальных условиях важное значение имеет среда, которая вносит аддитивные и мультипликативные помехи, искажая образ объекта. В таких условиях задача распознавания или обнаружения образов в вычислительных системах становится особенно актуальной. Существующие [5, 6] реальные линии связи (ЛС) существенно отличаются от моделей, построенных как численными методами, так и другими дифференциальными математическими моделями ввиду недетерминированности помех. Задача моделирования оптимального распознавателя становится практически неформализуемой. Для устранения влияния внешней среды используют различные методы помехоустойчивого кодирования [1, 2]. Введение кодеков приводит к необходимости применять сдвоенную схему обнаружения образов. В такой схеме на первом уровне производится обнаружение и оптимальная обработка данных на физическом уровне амплитуд. На втором уровне происходит декодирование информации и возможное исправление возникших после первой схемы ошибок. Максимальная корректирующая способность обусловлена тем или иным способом кодирования [1, 2, 6]. Кроме того, в оптимальных распознавателях образов необходимо учитывать наличие большого числа исходных образов, что усложняет сдвоенную схему многократно. Формализовать такую схему становится практически невозможно. Именно на решение подобных задач направлены НС, способные к адаптации к реальным условиям и решению практически не формализуемых задач на так называемом «интуитивном уровне».
Цель исследования: чтобы воспользоваться всеми преимуществами НС, необходимо устранить недостаток двойной схемы обработки – это отсутствие взаимосвязей между указанными схемами обработки. Первая схема использует свой критерий распознавания без учета тонких возможностей второй. Некоторые помехоустойчивые коды более устойчивы к пакетам ошибок, а другие – к периодическим или повторяющимся ошибкам. При этом в первой схеме не учитывается возможность изменения ее параметров, порога принятия решения. Вторая схема никак не может использовать дополнительную информацию, утраченную на уровне первой схемы, то есть учесть или распознать наличие постоянной помеховой составляющей, обусловленное влиянием других электромагнитных помех. Очевидным преимуществом использования НС при реализации оптимальных схем распознавания является возможность осуществлять прием информации в целом за счет объединения и интеграции обоих уровней в один на основе НС. Таким образом, цель исследования – устранить недостаток сдвоенной схемы обработки за счет интеграции НС в вычислительные элементы. Кроме того, расширим подход синтеза [7] на случай произвольного числа k образов.
Материалы и методы исследования
В качестве базовых моделей выбраны существующие структуры вычислительных систем. Важно, в качестве образа или сигнала используется произвольная последовательность двоичных импульсов, произвольной длительности, используемая в качестве образа. При этом распределение аддитивной помехи считается нормальным с гауссовским распределением амплитуд. В работе использованы методы математического моделирования оконечных вычислительных структур в нейросетевом базисе на основе интеграции математического аппарата нейронных сетей в алгоритмические модели систем распознавания образов. Для решения задачи рассмотрим классическую схему различения образов или сигналов и распространим ее на k образов. Синтез первой решающей схемы распознавания основан на схематической реализации аналитического отношения правдоподобия [2, 7]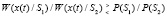 
, которую можно распространить на k образов Si как попарное сравнение отношений условных плотностей распределения 
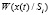и соответствующих априорных вероятностей P(Si) образов
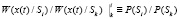, (1)
где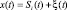 
– аддитивная смесь образа и шума ξ(t), – плотность распределения вероятностей аддитивной смеси при условии передачи Si образа, – априорная вероятность передачи Si образа. Общее решение в пользу того или другого образа может быть определено на основе тождественного максимального соответствия (1). Для непрерывного сигнала длительностью T, спектральной плотностью мощности шума N0 справедливо гауссовское распределение помехи и следовательно распределение аддитивной смеси
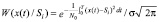. (2)
Подстановка (2) в (1) позволяет сформулировать правило принятия решения при распознавании. Примем энергии образов равными, тогда
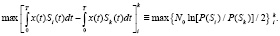(3)
Здесь операция max – означает процедуру выбора максимально соответствующего отношения, тождественно совпадающий с эталонным отношением. В выражении вычисляются попарные разности между (i, k) взаимокорреляционных функций приходящего образа x(t) и копий оригиналов образов Sk(t). Очевидно, что для дискретного образа данную задачу могут реализовать согласованные фильтры (СФ) [3, 7], вычисляющие корреляционную функцию. Очевидно, таких согласованных фильтров в отличие от [7] должно быть k в обнаружителе. Соответственно и функций корреляций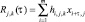 
, где xi – элемент дискретного образа, hi,j,k – дискретная импульсная характеристика фильтра Sk-го образа. Тогда выражение (3) примет вид
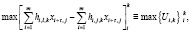(4)
где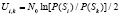 
– попарные отношения априорных вероятностей эталонных образов Si, m – число элементов в числе k образов. Операция max – выделение максимально соответствующего тождественного равенства. Именно ему будет соответствовать образ. Анализ (4) показывает, что схема оптимального устройства распознавания представляет собой обученную НС, где на основе выбранной функции активации принимается решение, по выбору соответствующего распознанного образа
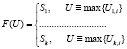. (5)
Пороговая функция активации [3] не позволяет эффективно использовать все возможности НС, позволяя свести матрицы весовых коэффициентов нейронов в одну. Поэтому для вычисления обратных связей или весовых коэффициентов в качестве функции активации можно использовать функцию активации сигмоид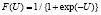 
. Очевидно, что реализация (4) может быть выполнена на основе самообучающейся нейронной сети. Выберем сеть прямого распространения с обучением по алгоритму Хэбба без учителя [2]. Такие фильтры имеют возможность динамически изменять весовые коэффициенты wij, выполняющие роль реальных импульсных характеристик hi,k с учетом реальной среды или помех. Для рассматриваемой НС и выбранного метода обучения используем итерационную формулу Хэбба обучения НС 
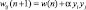, со скоростью обучения α. Тогда функция автокорреляции
.
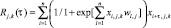С учетом принципов и алгоритмов построения НС для построения оптимального устройства распознавания k образов, реализующего (4), получим схему (рис. 1), отличающуюся от [7] наличием k обучающихся согласованных фильтров СФ. Кроме того, имеет место замена выходного порогового нейрона на блок вычисления порогов и определения максимума отношений, реализующий выражение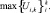 
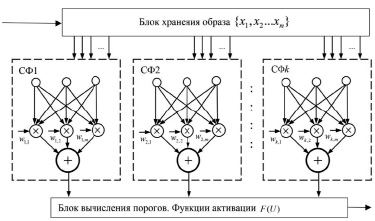
Рис. 1. Первая решающая схема в НС базисе
Очевидно, что все согласованные фильтры могут быть интегрированы в одну самообучающуюся нейронную сеть. Кроме того, для заранее известных эталонов образов, блок вычисления порогов, так же может быть реализован нейронной сетью Хопфилда в виде ассоциативной памяти с заранее известными образами. Это позволяет реализовывать алгоритмы обучения нейронной сети с учителем, а также использовать НС с обратным распространением. Функции активации могут иметь различный вид. Обычно используется сигмоидальный вид [7–9]. Влияние функций активации на эффективность сети подлежит дальнейшему исследованию. Преимуществом рассмотренной НС в отличие от согласованных фильтров является возможность параллельно обрабатывать данные из параллельного КС. Параллельными данными могут быть образы, представленные в параллельной математике, такой как система остаточных классов (СОК) [4].
Проанализируем вторую решающую схему, которая осуществляет помехоустойчивое кодирование и декодирование. Рассмотрим на примере линейного кодирования. Тогда из образов Sk составляется кодовая последовательность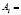 
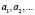, где l = 1…M, M – число разрешенных кодограмм. В общем, для ai,l – информационных символов кодограммы l, bi,l – проверочных символов, уравнения декодирования можно записать в виде
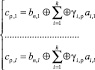, (6)
где γi,ρ – определяется ρ = 1…n – k уравнением кодирования. Очевидно, выражения (6) легко могут быть реализованы в НС, где основными операциями являются сложение и умножение. На рис. 2 можно представить такую НС. При этом в качестве анализатора синдрома можно использовать алгоритмический блок (АБ) нейронную сеть Хопфилда [3], реализующую двунаправленную ассоциативную память.
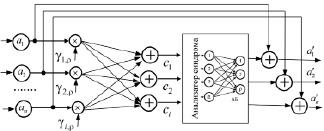
Рис. 2. Вторая решающая схема УР
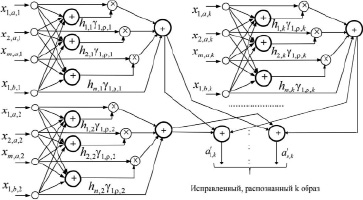
Рис. 3. Оптимальное устройство распознавания образов в НС базисе
Очевидно, для распознавания множества образов необходимо разбить общую НС на множество подобных решающих схем второго уровня. Для реализации распознавания образа в целом необходимо объединить НС (рис. 1) и НС (рис. 2) в одну сеть. Анализ выражений (4) и (6) показывает, что наличие однотипных алгебраических операций позволяет интегрировать их в единое аналитическое выражение. Решение о распознавании xi,j,k элемента k образа Sk принимается в момент тождественного совпадения разностей корреляционных функции, то есть при τ = 0. Каждому значению l в (6) соответствует совокупность из n элементов Sj принятого образа, то есть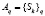 
. Обозначим элементы образа xi,a,k и xi,b,k, как элементы, из которых формируются информационные (a) и проверочные (b) символы эталонного (разрешенного) q образа (кодограммы). Далее опустим индекс q. Тогда подстановка выражения (4) в выражение (6) дает для k образа
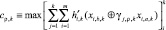, (7)
где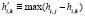 
импульсная характеристика того фильтра, где наблюдается максимум правдоподобия или максимальное соответствие исходному образу распознаваемой аддитивной смеси. Анализ последнего выражения показывает, что устройство распознавания (УР) легко может быть реализовано в нейросетевом базисе. Причем весовые коэффициенты в данном случае 
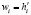являются результатом самообучения нейронной сети – аналога СФ. Более подробно реализация одного элемента для k образа представлена в [7]. С учетом большого числа образов НС усложняется. На рисунке многоточие подразумевает расширение НС до числа образов как на входе, так и на выходе 3. Для упрощения проверочные символы опущены.
Результаты исследования и их обсуждение
Выход сети для каждого элемента (рис. 3) является результатом интеграции НС согласно выражению (7). Если распределить ресурсы единой сети, то разделение на отдельные компоненты и блоки стирается. Образуется единая НС, способная к распознаванию и коррекции исходного образа. Получается сложная многослойная НС, полученная в результате интегрирования обучающихся участков и фиксированных (обученных) участков. При этом вектор ошибок для каждого образа уже будет не просто корректирующим вектором. В нем будут учтены как структура помехи, так и корреляционные свойства исходного образа. Образ будет распознаваться «в целом», а не поэлементно. Задача решена.
Выводы
Представлен подход к синтезу нейронной сети распознавания образов «в целом». Сеть, построенная согласно (4, 6, 7) на основании расширения оптимального приемника отдельных элементов [7], до схемы распознавания k образов за один такт работы НС. Для упрощения реализации схемы в работе были сделаны допущения при выборе оптимальных схем решения, линейных алгоритмов кодирования и достаточно простых, линейных алгоритмов обучения без учителя. Это позволило сделать процедуру синтеза более наглядной и не ограничивает сам подход на расширение ее свойств. При этом НС должна быть обучена заранее на исходные образы. Используя предложенный подход, существует возможность реализации и других элементов вычислительных систем. Открытым остается выбор функций активаций и алгоритмов обучения.