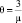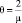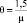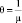Поллинговые системы, то есть системы массового обслуживания, где единственное обслуживающее устройство обрабатывает заявки, накапливающиеся в нескольких независимо формирующихся очередях, известны давно. Одна из первых публикаций, посвященная этой проблематике, работа Лейбовица [1], датирована еще 1961 г. В последние два десятилетия интерес к таким системам значительно вырос. Это обусловлено прежде всего бурным развитием телекоммуникационных технологий и компьютерных сетей, работа которых построена таким образом, что одно обслуживающее устройство (сервер) принимает в установленном порядке пакеты информации от нескольких несвязанных между собой источников. Растущий интерес научного сообщества к поллинговым системам подтверждается значительным числом опубликованных результатов исследований в этой области [2–5], касающихся различных аспектов построения и функционирования таких систем. Важность и оригинальность этих работ характеризует, в частности, тот факт, что наряду с известным аппаратом метода производящих функций, специально для анализа поллинговых структур, были разработаны и применены такие новые приёмы, как метод ветвящихся процессов и метод анализа средних. В целом математический аппарат, используемый для описания поллинговых систем, весьма совершенен, а конечной результат представляет собой итог изящных, но не всегда очевидных рассуждений и умозаключений.
Общей особенностью практически всех сложных и содержательных моделей систем массового обслуживания и поллинговых систем в частности является то, что при их построении используются параметры, которые априори, как правило, не известны, а их экспериментальное определение трудноосуществимо. Это существенно снижает востребованность таких моделей применительно к решению прикладных задач. Важно также отметить, что приоритетом практически всех моделей систем массового обслуживания выступают интересы пользователей, а конечным результатом моделирования оказываются такие показатели, как длина очереди, время ожидания и т.п., для достижения желаемого значения которых подбираются различные варианты обслуживания, опроса, дисциплины очереди. При этом по умолчанию предполагается, что для администратора все эти варианты равноприемлемы, хотя, конечно, на самом деле это не так. И поскольку, как было показано в работе [6], технико-экономические характеристики поллинговых систем, функционирующих в шлюзовом и исчерпывающем режимах обслуживания, практически неразличимы, возможности влияния на ситуацию со стороны администратора оказываются ничтожными. Следует упомянуть и о том, что использование большинства математических моделей в составе расчетных схем возможно только для потоков с простейшими однопараметрическими функциями распределения. В любом другом случае получение решения даже с помощью численных алгоритмов является весьма сложной задачей.
Постановка задачи исследования
В последнее время значительное внимание исследователей привлекают системы с ограниченным временем жизни заявок, где в силу природных, технических или организационных причин назначается предельное время пребывания заявок на обслуживании, по истечении которого заявка покидает систему независимо от того, было ли завершено ее обслуживание или нет. Математическое моделирование и расчет подобных систем сложны и трудоемки [7], поскольку привычный вид функций распределения заявок в потоке существенно меняется. Однако если лимит времени устанавливается директивно, то есть имеет организационный порядок, – то это открывает дополнительные, весьма широкие возможности администрирования. Предметом данной статьи является математическое и имитационное моделирование поллинговых систем с ограниченным временем жизни заявок и разработка приёмов эффективного администрирования таких систем.
Математическая модель
Рассмотрим математическую модель поллинговой системы, функционирующей в исчерпывающем режиме обслуживания, построенную методом анализа средних, как рекомендовано в монографии [8]. Пусть система имеет в своем составе N независимых очередей. Обозначим комбинацией символов (i, j) период времени, охватывающий посещение обслуживающим устройством с i-й очереди по j-ю в порядке циклического обхода. Тогда безусловная длина i-й очереди Li выразится как
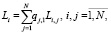 (1)
(1)
где qj1 – вероятность того, что в произвольный момент времени обслуживающее устройство находится в j-й очереди; Li,j – длина i-й очереди в момент нахождения обслуживающего устройства в j-й очереди. Символом qi,j будем обозначать долю времени, когда система пребывает в периоде (i, j), предполагая, что в стационарном режиме эта величина не изменяется от цикла к циклу.
Величины Li,j определяются путем решения системы линейных уравнений
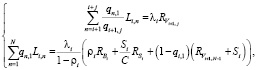 (2)
(2)
где λi – интенсивность потока пополнения i-й очереди; 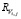 – среднее оставшееся время (i, j) периода;
– среднее оставшееся время (i, j) периода; 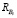 – среднее оставшееся время обслуживания заявок в i-й очереди; ρi – коэффициент загрузки i-й очереди; Si – случайная величина, характеризующая время пребывания обслуживающего устройства в i-й очереди;
– среднее оставшееся время обслуживания заявок в i-й очереди; ρi – коэффициент загрузки i-й очереди; Si – случайная величина, характеризующая время пребывания обслуживающего устройства в i-й очереди; 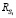 – остаточное время переключения на i-ю очередь; C – общее время цикла; Bi – случайная величина, характеризующая время обслуживания заявки в i-й очереди. Величины
– остаточное время переключения на i-ю очередь; C – общее время цикла; Bi – случайная величина, характеризующая время обслуживания заявки в i-й очереди. Величины 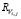 вычисляются по соотношению
вычисляются по соотношению
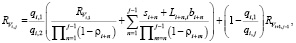 (3)
(3)
для чего предварительно находится
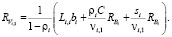 (4)
(4)
Здесь vi,j – средняя длительность периода (i, j); bi – первый момент функции распределения потока, пополняющего i-ю очередь.
Для систем, функционирующих в режиме шлюзового обслуживания, базовое расчетное соотношение для отыскания величин Li,j остается справедливым, однако формулы (3) и (4) претерпевают изменения
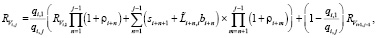 (5)
(5)
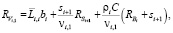 (6)
(6)
где 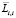 – заявки, обслуживаемые в текущем цикле;
– заявки, обслуживаемые в текущем цикле; 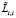 – заявки, поступившие в очередь в ходе обслуживания. Естественно, что
– заявки, поступившие в очередь в ходе обслуживания. Естественно, что
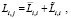 (7)
(7)
а безусловная длина i-ой очереди при шлюзовом варианте обслуживания
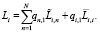 (8)
(8)
Решение системы уравнений (2) задача хотя и трудоёмкая, но не сложная. Главную сложность представляет идентификация выражений (3)–(6). Отыскание и оценка таких параметров, как qi,j, 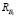 ,
, 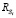 ,
, 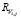 , является не простой, отдельной проблемой и оказывается основным препятствием на пути практического использования представленных моделей. Именно это побудило авторов, стремившихся к получению не только достоверных, но и реализуемых результатов, применить в своем исследовании аппарат имитационного моделирования.
, является не простой, отдельной проблемой и оказывается основным препятствием на пути практического использования представленных моделей. Именно это побудило авторов, стремившихся к получению не только достоверных, но и реализуемых результатов, применить в своем исследовании аппарат имитационного моделирования.
В качестве предмета имитационного моделирования была выбрана поллинговая система массового обслуживания, имеющая в своем составе четыре независимые очереди, пополнение которых происходит пуассоновскими потоками заявок с интенсивностями 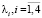 . Предполагается, что обход очередей обслуживающим устройством выполняется циклически без затрат времени на переход от одной очереди к другой.
. Предполагается, что обход очередей обслуживающим устройством выполняется циклически без затрат времени на переход от одной очереди к другой.
Рассмотрим ситуацию, когда поток обслуживания распределен экспоненциально и имеет одинаковую интенсивность μ для заявок любой очереди. При этом устанавливается предельное время пребывания заявок в стадии обслуживания ?, по достижении которого их обслуживание прекращается, а заявки либо удаляются из системы, либо снова помещаются в ту же очередь. Это самым существенным образом меняет вид функции распределения. Она приобретает конечный размах [0, ?] и, если представить возникшие изменения на гистограмме, то это выразится в присоединении всех разрядных частот, больших ?, к разряду, для которого величина ? является правой границей (см. рис. 1).
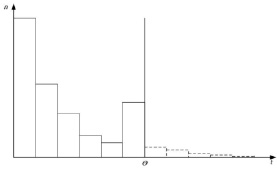
Рис. 1. Гистограмма функции распределения потока с ограниченным временем жизни заявок. Пунктиром отмечены разряды, превосходящие ?
Наиболее близкий аналог этого распределения, аналитическое выражение которого известно, можно отыскать среди так называемых кривых Пирсона [9]. Это обширное семейство функций, порождаемое решениями дифференциального уравнения
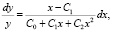 (9)
(9)
общий интеграл которого может быть записан в виде
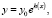 (10)
(10)
где
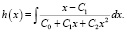 (11)
(11)
Постоянные, входящие в состав подынтегрального выражения (11), определяются через моменты распределения
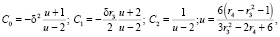 (12)
(12)
где r3 и r4 – третий и четвертый основные моменты распределения.
Нас будет интересовать случай, когда корни знаменателя подынтегрального выражения действительны и различны по знаку. Это выполняется при условии
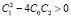 и C0C2 < 0, (13)
и C0C2 < 0, (13)
а функция плотности вероятности искомого распределения имеет вид
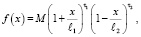 (14)
(14)
где M – нормировочный множитель.
Значения параметров τ1, τ2, ?1, ?2 также определяются с помощью моментов распределения
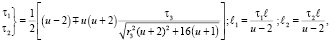 (15)
(15)
где ? – размах распределения. И если τ1 и τ2 ∈ (–1, 0), то функция плотности вероятности имеет вид, представленный на рис. 2.
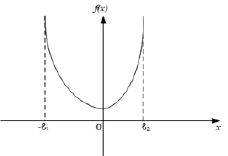
Рис. 2. График функции распределения, задаваемой соотношением (14)
Предполагается, что случайная величина x центрирована так, что в точке x = 0 функция f(x) достигает своего минимального значения.
Имитационная модель и обсуждение ее результатов
Функция распределения плотности вероятности (14) дает описание сложного многопараметрического распределения, идентификация параметров которого требует вычисления четырех основных моментов. Поэтому применение его в вычислительных схемах, в частности, для определения параметров системы уравнений (3)–(6), представляется малоперспективным. С помощью имитационного моделирования эти затруднения преодолеваются, поскольку оно позволяет осуществить численный анализ сколь угодно сложного процесса, минуя стадию аналитического сопровождения.
Используя средства имитационного моделирования, мы проследили, как изменятся технико-экономические и эксплуатационные характеристики поллинговой системы с четырьмя независимыми очередями после введения ограничений на время жизни заявок в пуассоновском потоке обслуживания. Прежде всего, рассмотрим как с введением ограничений на время пребывания заявок в стадии обслуживания изменяется величина свободного времени обслуживающего устройства, что для любых систем является важнейшим технико-экономическим показателем. В табл. 1 приведены результаты имитационного эксперимента, целью которого была количественная оценка описанных изменений для различных вариантов организации обслуживания и пополнения очередей внутри поллинговой системы.
Таблица 1
Результаты имитационного моделирования поллинговой системы с ограничением времени жизни заявок
|
Предельное время обслуживания |
Интенсивности потоков пополнения очередей |
Шлюзовое обслуж. |
Исчерпывающее обслуж. |
Количество «отрезанных» заявок одноканальной системы % |
||
|
Количество «отрезанных» заявок % |
Свободное время обслуживающего устройства % |
Количество «отрезанных» заявок % |
Свободное время обслуживающего устройства % |
|||
|
|
λ = (1,2,3,4) |
5,10 |
4,36 |
5,00 |
4,31 |
4,98 |
|
λ = (2.5,2.5,2.5,2.5) |
5,05 |
4,71 |
5,14 |
4,45 |
||
|
λ = (7,1,1,1) |
5,05 |
5,44 |
5,07 |
4,98 |
||
|
|
λ = (1,2,3,4) |
13,88 |
12,68 |
13,80 |
12,57 |
13,54 |
|
λ = (2.5,2.5,2.5,2.5) |
13,63 |
13,89 |
13,79 |
14,01 |
||
|
λ = (7,1,1,1) |
13,80 |
13,54 |
13,86 |
13,14 |
||
|
|
λ = (1,2,3,4) |
22,43 |
22,58 |
22,50 |
22,44 |
22,32 |
|
λ = (2.5,2.5,2.5,2.5) |
22,39 |
22,75 |
22,37 |
22,72 |
||
|
λ = (7,1,1,1) |
22,50 |
21,95 |
22,27 |
22,87 |
||
|
|
λ = (1,2,3,4) |
36,64 |
36,88 |
36,61 |
36,94 |
36,79 |
|
λ = (2.5,2.5,2.5,2.5) |
37,02 |
36,82 |
36,84 |
36,47 |
||
|
λ = (7,1,1,1) |
36,78 |
36,79 |
36,64 |
37,15 |
||
Анализ данных, представленных в таблице, показывает, что по мере сокращения времени жизни заявок ? заметно растет количество заявок, покидающих систему в связи с исчерпанием лимита времени ?, а вместе с этим увеличивается доля времени, в течение которого обслуживающее устройство оказывается свободным. Важным, на наш взгляд, является тот факт, что эти величины практически одинаковы и для исчерпывающего, и для шлюзового варианта обслуживания. Заметим также, что доля заявок, покинувших систему до завершения обслуживания, совпадает с точностью до 1 % с аналогичным показателем для системы массового обслуживания с одной очередью, который был вычислен по известному расчетному соотношению. Это полностью согласуется с выводами, сделанными авторами в работе [6], о том, что поллинговая система выполняет функцию усреднения по ансамблю и что для оценки ряда технико-экономических характеристик поллинговых систем можно использовать формулы, описывающие поведение традиционных систем массового обслуживания.
Введение ограничения на время жизни заявок, как упоминалось выше, расширяет возможности администрирования. При наличии резерва свободного времени обслуживающее устройство может быть выведено из эксплуатации для проведения планового профилактического осмотра, мелкого ремонта и т.п. без ущерба для его основной деятельности. Из материалов табл. 1 видно также, что если 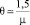 , величина ресурса свободного времени обслуживающего устройства, становится достаточной для организации дополнительной очереди. Действительно, если резерв свободного времени превышает 20 %, то это означает, что на обработку потока заявок от четырех очередей обслуживающее устройство затрачивает только 80 % рабочего времени. Таким образом, возникает возможность подключения к обслуживанию еще одной очереди, интенсивность пополнения которой равна среднему арифметическому интенсивностей четырех очередей, изначально входивших в состав поллинговой системы.
, величина ресурса свободного времени обслуживающего устройства, становится достаточной для организации дополнительной очереди. Действительно, если резерв свободного времени превышает 20 %, то это означает, что на обработку потока заявок от четырех очередей обслуживающее устройство затрачивает только 80 % рабочего времени. Таким образом, возникает возможность подключения к обслуживанию еще одной очереди, интенсивность пополнения которой равна среднему арифметическому интенсивностей четырех очередей, изначально входивших в состав поллинговой системы.
Еще одной целью имитационного моделирования в настоящей работе была оценка длин очередей и характера их изменения при введении ограничений на время жизни заявок. Это один из важнейших эксплуатационных показателей любых систем массового обслуживания, причем для пользователей он, несомненно, является приоритетным. Результаты имитационных экспериментов, реализованных в среде AnyLogic, представлены в табл. 2.
Таблица 2
Длины очередей поллинговой системы
|
Интенсивности потоков пополнения очередей |
Длины очередей |
|||||||||
|
Исчерпывающее обслуживание |
Шлюзовое обслуживание |
|||||||||
|
L1 |
L2 |
L3 |
L4 |
Lсумма |
L1 |
L2 |
L3 |
L4 |
Lсумма |
|
|
λ = (2.5,2.5,2.5,2.5), µ = 12, без среза |
1,787 |
1,743 |
1,779 |
1,749 |
7,058 |
1,817 |
1,809 |
1,747 |
1,798 |
7,172 |
|
λ = (2.5,2.5,2.5,2.5), µ = 10, без среза |
35,24 |
35,87 |
35,19 |
35,47 |
141,77 |
23,64 |
22,67 |
24,12 |
23,95 |
94,37 |
|
λ = (2.5,2.5,2.5,2.5), µ = 10, tсреза = 1,5/µ = 0,15 |
1,338 |
1,397 |
1,318 |
1,372 |
5,426 |
1,303 |
1,279 |
1,367 |
1,378 |
5,327 |
|
λ = (2.5,2.5,2.5,2.5), µ = 10, tсреза = 2/µ = 0,2 |
1,907 |
1,853 |
1,833 |
1,891 |
7,485 |
2,094 |
2,122 |
2,073 |
2,149 |
8,438 |
|
λ = (1,2,3,4), µ = 12, без среза |
1,00 |
1,843 |
2,618 |
3,273 |
8,733 |
0,691 |
1,641 |
2,463 |
3,613 |
8,408 |
|
λ = (1,2,3,4), µ = 10, без среза |
24,85 |
44,18 |
58,71 |
68,94 |
196,67 |
7,76 |
16,59 |
26,89 |
38,67 |
89,89 |
|
λ = (1,2,3,4), µ = 10, tсреза = 1,5/µ = 0,15 |
0,713 |
1,369 |
1,953 |
2,744 |
6,779 |
0,584 |
1,313 |
1,936 |
2,838 |
6,672 |
|
λ = (1,2,3,4), µ = 10, tсреза = 2/µ = 0,2 |
1,262 |
2,574 |
3,478 |
4,353 |
11,668 |
0,865 |
2,00 |
3,007 |
4,375 |
10,247 |
|
λ = (7,1,1,1), µ = 12, без среза |
6,357 |
1,863 |
1,602 |
1,551 |
11,373 |
9,816 |
1,033 |
1,101 |
0,987 |
12,938 |
|
λ = (7,1,1,1), µ = 10, без среза |
82,30 |
34,55 |
35,59 |
36,89 |
189,34 |
117,8 |
11,49 |
11,56 |
10,61 |
151,46 |
|
λ = (7,1,1,1), µ = 10, tсреза = 1,5/µ = 0,15 |
6,383 |
1,495 |
1,469 |
1,277 |
10,625 |
7,177 |
0,797 |
0,768 |
0,708 |
9,449 |
|
λ = (7,1,1,1), µ = 10, tсреза = 2/µ = 0,2 |
6,838 |
2,026 |
1,972 |
1,794 |
12,629 |
8,751 |
0,84 |
8,36 |
8,49 |
11,275 |
Как и следовало ожидать, ограничение времени пребывания заявок в стадии обслуживания значительно сокращает длины очередей поллинговой системы. Фактически из материалов табл. 2 ясно видно, что это эквивалентно соответствующему увеличению интенсивности потока обслуживания. Так, введение ограничения времени жизни заявок до 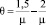 дает примерно такой же эффект, как увеличение интенсивности обслуживания μ с 10 до 12. Заметим в очередной раз, что и на длину очереди поллинговой системы изменение режима обслуживания не оказывает сколько-нибудь заметного влияния. Это позволяет не принимать во внимание данный фактор при решении задач администрирования.
дает примерно такой же эффект, как увеличение интенсивности обслуживания μ с 10 до 12. Заметим в очередной раз, что и на длину очереди поллинговой системы изменение режима обслуживания не оказывает сколько-нибудь заметного влияния. Это позволяет не принимать во внимание данный фактор при решении задач администрирования.
Интересным результатом имитационного моделирования, на наш взгляд, является тот факт, что между длинами очередей поллинговых систем в целом с различными интенсивностями потоков пополнения обнаруживается заметное различие. Это можно объяснить тем, что при рассмотрении работы обслуживающего устройства наблюдаемое усреднение поступающих заявок осуществлялось по ансамблю. При анализе же процесса изменения длин очередей начинает проявляться влияние фактора времени через различие интенсивностей входных потоков заявок. Таким образом, для поллинговых систем среднее по ансамблю не может быть отождествлено с усреднением по времени. Отсюда следует, что для систем поллинга гипотезу эргодичности средствами имитационного моделирования подтвердить не удается.
Выводы
1. Построены имитационные модели поллинговых систем с ограниченным временем жизни заявок.
2. В рамках этой модели предложен вид функции распределения потока обслуживания и установлено ее аналитическое выражение.
3. Доказано, что перераспределение интенсивностей входных потоков пополнения очередей не влияет на эксплуатационные свойства системы, функционирующей как в шлюзовом, так и в исчерпывающем режимах.
4. Расширены возможности администрирования, в частности исследована возможность подключения к обслуживанию дополнительной очереди.