В работе исследуются некоторые операторы и операторные уравнения в пространстве программ, которые полезны при построении и изучении формальных семейств программ, верификации, оценки их сложности.
В [1, с. 14] рассмотрены некоторые операторные уравнения A(x) = y в пространстве программ М над алфавитами X и Y, M(Pi), i = 1, 2,… – множество программ которые реализуют одну задачу Pi, введены понятия сходимости, на базе которых рассмотрены операторы минимизации Ad, Af, At по числу операндов d(x), ператоров f(x), времени программирования t(x) программы x, соответственно, с критериями: Ad(x) = y,∀z∈P: d(y) ≤ d(z); Af(x) = y, ∀z∈P: f(y) ≤ f(z);At(x) = y, ∀z∈P: t(y) ≤ t(z).. Но необходимая в теоретическом аспекте проблема исследования разрешимости операторных уравнений над пространствами программ не была исследована. Цель данной работы – исследовать разрешимость таких уравнений. Применяются методы функционального анализа, операторов сжатия и др. Рассматриваются и практические характеристики операторных уравнений, например оцениваются время, длина, сложность, устойчивость и другие. Методами системного анализа проведена аксиоматизация меры сложности модулей.
Время оцениваемо различными способами [2, с. 80], например по Холстеду:
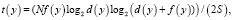
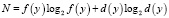– длина программы, S – число Страуда.
Продемонстрируем действие At на фрагменте программы решения ax2 + bx + c = 0 (ищем действительные корни, описания, оптимальность не акцентируется):
read(a, b, c); d:=sqr(b)–4*a*c;
if (d<0) then write(‘нет корней’)
else begin
x1:=(–b + sqrt(d) ) / (2*a); x2:=(–b – sqrt(d)) / (2*a);
if (d=0) then write(‘кратный корень x=’,x1)
else write(‘корни x1=’, x1,’, x2=’, x2)
end;
Итак, количество операндов равно 14 (a, b, c, d, 2, 0, 4, x, x1, x2 и четыре текста вывода); количество типов операторов – 16 («write», «read», «if – then – else», «:=», «/», «*», «–», «+», «<», «=», «sqr», «sqrt», «()», «;», «begin», «end»). При среднем значении S=18 (обычно 3 < S < 25) получаем t ≈ 972 сек.
Заменяя все вхождения не входных-выходных переменных d, x, x1, x2 на соответствующие выражения, получим
read(a, b, c);
if (sqr(b) – 4*a*c < 0) then write(‘корней нет’) else begin
if (sqr(b) – 4*a*c = 0) then write(‘кратный корень=’,–b/(2*a))
else if (sqr(b) – 4*a*c > 0) then
write(‘x1=’,(–b–sqrt(sqr(b)–4*a*c))/(2*a),‘x2=’,(–b+sqrt(sqr(b)–4*a*c))/(2*a));
end;
Для 16 операторов, 8 операндов, фиксируем новое время t = 538 сек. Время уменьшилось почти вдвое. Можно далее «вывести из программы» оператор sqr, вводя оператор D:= b*b–4*a*c; и уменьшить еще несколько время. Но оптимальный вариант программы, естественно, – по оптимальному алгоритму. В этой простой задаче можно предложить вариант, в котором используется основной блок вида:
if (sqr(b) – 4*a*c < 0) then write(‘нет корней’)
else if (sqr(b) – 4*a*c = 0)
then write(‘кратный корень x=’,–b/(2*a)) else begin
x1:=–b/(2*a); x2:=x1*x1–с/а;
if(x2>0) then begin
x2:=sqrt(x2); x1:=x1–x2; x2:=x1+2*x2; write(‘x1=’,x1,‘x2=’,x2)
end;
Затрачено меньше операций и операндов, чем в классическом алгоритме. И, хотя время уже уменьшилось лишь немного (до 455 сек), отметим, что «сэкономлены» наиболее длительные (с точки зрения микропрограммной реализации) операции – вычитание, вычисление корня, умножение.
Пространства программ, операторы над ними и их свойства
Рассмотрим множество программ M с несовпадающими входными множествами, например, решающих одну задачу различными методами. В пространстве X элементов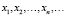 
вводится метрика
,
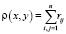n – количество модулей в x, y, rij – веса дуг орграфа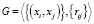 
.
Разобьем M на M1, M2,…, Mi ≠ ∅, Mi∩Mj= ∅, чтобы в каждое подмножество попали программы, рассматриваемые (разрабатываемые) одинаковым методом. На множестве M* оптимальных, минимизированных по вышеприведенным критериям программ на Mi, i = 1, 2,… выберем некоторую оптимальную по рассматриваемому параметру (длина, время, объем, полнота тестирования, сложность, устойчивость и др.) программу.
Рассмотрим вопрос о существовании и единственности неподвижной точки. Для оператора Ad (Af, At) она существует. Действительно, для любой программы х можно составить последовательность программ Xi+1 = A(Xi), X0 = X, i = 1, 2,…, тогда для любого i выполняется условие
,
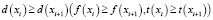но функция d(x) (f(x), t(x)) ограничена снизу нулем. Следовательно,
,
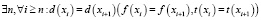т.е. A(xn) = xn и xn – неподвижная точка.
Реальный объем программы V – количество информации (бит), необходимое для записи программы на выбранном языке программирования. Минимальный объем программы Vi – минимальное количество информации (бит), необходимое для записи программы без учета конкретного языка программирования. Очевидно, Vl = min V, где {L} – множество языков программирования. Если реальный объем равен минимальному объему (количество операндов равно количеству входных-выходных переменных и количество типов операторов равно двум – существующая, реализующая цель программы и присваивания результатов функции выходным переменным), то стационарная точка существует (данная программа минимальна по f и по d).
Рассмотрим случай, когда реальный объем больше минимального. Выберем множество Pm из P такое, что для любой программы из Pm при любом уменьшении количества операндов увеличивается количество типов операторов и, наоборот, при уменьшении количества типов операторов увеличивается количество операндов. Докажем, что такое непустое Pm существует.
Пусть A1 – уменьшение операндов программы на единицу, а A2 – уменьшение типов операторов программы на единицу. Процедура действия оператора A1: выбираем переменную, которая не является входной-выходной, находим ее значение (текущее значение переменной – «формулу») и заменяем все вхождения переменной-операнда на ее выражение. Процедура действия A2: если возможно, выражаем выбранный оператор через остальные используемые операторы и переменные, затем подставляем найденное выражение вместо выбранного оператора, если это невозможно – конец.
Для программы x∈P составим последовательность {xi}: xi+1 = A(xi), x0 = x. Так как d(xi) убывает и d(xi) ограничено снизу, то {xi} сходится к некоторой программе X. Объединим такие программы X во множество P* (оно не пустое, оператор A1 существует для любого xi). Для программы y∈P* составим последовательность {yi}: yi+1 = A2(yi), y0 = y. Так как f(yi) убывает и f(yi) ограничено снизу, то {yi} сходится к некоторой программе Y. Объединение таких программ во множество и есть множество Pm. Конструктивное построение Pm и A2 для любой программы yi дает, что множества не пусты. Теперь Pm принадлежит P и для любого х и P: A(x) = y, где y∈Pm, т.е. Pm = infPm из определений A1, A2, Pm.
Рассмотрим уравнение A(x) = y и функцию V(x) получения какой-либо характеристики программы х. Следовательно, V(y) ограничено (снизу – нулем, сверху – V(x)), как и оператор A. Если вход-выход постоянен (для любых программ x, y из любого D входного множества x(D) = y(D)), то оператор A монотонен, так как в этом случае A(x) = A(y). Иначе, например, если используются различные алгоритмы, то оператор A – не монотонен.
Оператор линейный по функции (цели), нелинейный по структуре: A(x + y) = A(x) + A(y), A(B(x)) = B(A(x)). Если фрагмент Ni принадлежит и х, и у, то в программе A(x + y) он присутствует только один раз, а в программе A(x) + A(y) два раза (в A(x) и в A(y)).
Обратный оператор не существует. Корректность, надежность, структурированность, тестируемость и другие параметры программы зависят от сложности программы. Она определяется различными способами. Если Acj – оператор минимизации сложности программы, то Acj(z) = Bcj(z) означает, что по критерию Cj результаты действия операторов Acj и Bcj на программу z одинаковы, т.е. Cj(Acj(z)) = Cj(Bcj(z)).
Если оператор А – монотонный, отображает полную структуру программ Р в себя, то существует его неподвижная точка а: A(a) = a.
Действительно, B = {b:b∈P, b ≤ A(b)} ≠ ∅ в силу полноты (существования нуля из В). Следовательно, ?∃a = sup B, ∀b∈P:A(a) ≥ A(b) ≥ b, поэтому A(A(a)) ≥ A(a). Отсюда, A(a)∈P, a ≥ A(a). Из последних неравенств: A(a) = a.
Сложность программ (программных структур) и ее оценка
Сложность системы может быть различного типа и формы, но нас в работе интересуют больше формы.
Представление в форме орграфа. Представим логическую схему программы орграфом: вершины – модули, ребра – их связи, C1(x) – сложность программы, которую примем равной количеству ребер орграфа. Введем оператор Ac1: Ac1(x) = y, если для любого z из P: C1(y) = C1(z).
Любую программу можно структурировать (например, [3, с. 1]), поэтому оператор Ac1 cуществует. Он единственен: для C1 – оптимальной программы x нет модулей с одинаковыми целями, все связи между модулями необходимы и их минимальное количество, т.е. C1(x) = min C1(y), y∈P. Поэтому Ac1(x) = x и неподвижная точка существует.
Сложность структурированной программы меньше сложности неструктурированной, которая не может быть больше максимального количества связей: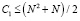 
, где N – количество модулей в программе. Следовательно, оператор Ac1 ограничен. Оператор Ac1 монотонен – для множества программ P результат действия оператора – одна программа. Оператор Ac1 нелинейный, условие Ac1(x + y) = Ac1 + Ac1(y) не выполняется: если фрагмент Ni принадлежит и программе х и программе y, тогда в программе Ac1(x + y) он присутствует только один раз, а в программе Ac1(x) + Ac1(y) два раза (в Ac1(x) и в Ac1(y)).
Обратный оператор существует, но не однозначен, достаточно ввести в C1 – оптимальную программу модуль-«заглушку» и рассмотреть программу zi, вызывающую новый модуль, тогда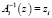 
, но и 
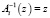, так как Ai(z) = z и Ai(zi) = z.
Критерий C1 и Ac1 лучше использовать при сложных взаимосвязях модулей, в многомодульных программах.
Представление в форме дерева. Пусть в программе N модулей и S связей, тогда минимальное количество связей модулей равно N – 1. Введем сложность C2(x) как относительную разницу реального и минимального количества связей: C2(x) = (S – N + 1)/(N – 1) и оператор минимизации сложности Ac2: Ac2(x) = y, ∀z∈P: C2(y) ≤ C2(z). Оператор Ac2 приводит структуру программы к древовидному виду. Для согласования связей возможно введение новых модулей.
Возьмем произвольную программу x, подействуем Ac2, получим y = Ac2(x) – программу с древовидной структурой. Тогда y = Ac2(y) и программа y – стационарная точка оператора Ac2. Для любой программы х C2(Ac2(x)) = 0, поэтому оператор ограничен снизу нулем; сверху ограничен значением C2(x) и, следовательно, оператор Ac2 ограничен. Для любой программы х из множества программ P, достигающих одну цель, результат действия оператора Ac2 – одна программа, и если z∈P, y = Ac2(z), то тогда ∀x∈P: y = Ac2(x).
Оператор Ac2 линеен, имеет обратный оператор, но он не однозначный. Критерий C2, оператор Ac2 эффективны, когда программа небольшая, необходимо вводить новые модули, она подвержена частым модификациям, содержит сложную обработку данных при сравнительно простых логических связях модулей.
Представление вектор-функцией. Положим Bik = 1, если в i-м модуле определяется (используется) k-я глобальная переменная; иначе – Bik = 0. Обозначим F(x) – вектор сложности программы, вектор-функция, длина которой равна количеству глобальных переменных. Пусть F(x)k равно сумме Bik по всем i. Сложность программы C3(x) оценим суммой F(x)k по всем k. Введем такой оператор Ac3, что Ac3 (x) = y и ∀z∈P:C3(y) ≤ C3(z).
Существование, ограниченность оператора Ac3 следует из принципов ООП, причем ∀x, y∈P: C3(x) ≤ C3(y) получим: C3(Ac3(x)) = 0,C3(Ac3(y)) = 0, C3(Ac3(x)) ≤ C3(Ac3 ( y)). Оператор – линейный, обратимый (не однозначно). Критерий C3 лучше использовать для написания программ на процедурных языках, он показывает, как хорошо задействованы языковые возможности структурирования программ. У хороших программ C3(x) равно примерно 3v, где v – количество глобальных переменных. В объектно-ориентированных языках программирования применение C3 не имеет смысла: почти все программы по нему оптимальны.
Две программы – эквивалентны (пока без уточнения – функционально или структурно, в общем, – по цели), если у них одинаковые цели, элементы, структура, а также можно конструктивно установить отношение «релевантности» (строго говоря, эквивалентности). Процедура выбора определяет на множестве M бинарное отношение типа «релевантность» (обозначим ≈). Можно распространить локальное отношение «релевантность» на всё многообразие M. Оно удовлетворяет свойствам (аксиомам) рефлексивности, симметричности, транзитивности, однозначности (две программы одинаковые по цели, результату – релевантны), непрерывности (мало отличающиеся по цели, структуре программы, незначительно отличаются по релевантности).
Для построения «дерева релевантности» можно применить следующую процедуру. Входные данные: непустые множества – программ P, буфер B, пустой изначально путь в дереве D (список). Процедура:
repeat
удаление из P программ, не отвечающих критериям релевантности D, помещая их в B;
добавление в Р и удаление из В программ, удовлетворяющих D;
if(D ≠ ∅) then if (значения последнего атрибута в D обработаны)
then изменить в D значение последнего параметра следующим
else удалить последний атрибут из D;
if (все программы из одного класса)
then добавить к D лист, содержащий идентификатор класса;
else определяется атрибут с наименьшей мерой релевантности;
добавить в D значение, наилучшее по релевантности;
until (D = ∅).
Метрик программ – много [4, c. 53]. Их можно разбить на классы:
- по сложности (например, информационной, структурной);
- надежности (устойчивые, самовосстанавливающиеся и др.);
- производительности программы;
- производительности программирования [5, с. 162];
- уровню языка (микрооперации, высокого уровня, запросов и др.);
- модифицируемости (кросс-платформенности, модульности) и др.
Часто рассматриваются меры, базирующиеся на понятии цели, например мера А. Харкевича (причинно-следственной обусловленности): если po, p1 – вероятности достижения критерия до и после получения информации о состоянии системы, то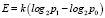 
. Применимы также общесистемные меры Н. Моисеева (мера релевантного управления), меры, учитывающие привлекаемые ресурсы типа Шеннона – Уивера, Маргалефа, Симпсона, Макинтоша и др. Широко применимы и проблемно-ориентированные меры – метрики Холстеда, Джилба, Майерса и др.
Метрики «опасны», как любая статистика по данным, распределение которых априори неизвестно полностью. Сотни метрик – разнородные, оценивают ПО, условия разработки, отклонения от норм, спецификаций и др. Наиболее важными являются метрики сложности (информационной, структурной, верификационной, языковой, прогнозной).
Аксиоматизация меры m сложности модульных структур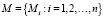 
может быть проведена на основе аксиом, аналогичных общесистемным, общефункциональным [6, с. 132]:
1) неотрицательность вводимой меры –
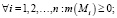
2) существование программы с нулевой мерой –
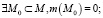
3) мера программы меньше меры всего комплекса –
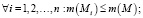
4) мера параллельно выполняемого комплекса –
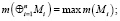
5) мера последовательно выполняемого комплекса –
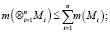
6) мера сложности вызова модуля –
,
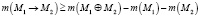где M1 > M2 – вызов модулем M1 модуля M2.
Выводы
В работе получены математические результаты (существование, единственность, релевантность, сложность), которые помогут формализовать и структурировать оценочную систему в программировании, провести верификацию, повысить релевантность и снизить алгоритмическую сложность программ. Метрическая теория программ – инструментарий практического исследования метрических качеств программ, верификации программ. Проведена аксиоматизация формальной сложности программ. Она может быть использована при построении формальной теории оценивания сложности программ в соответствующих пространствах программ.