Горные массивы в большинстве своем являются неоднородными по составу. Как показывает практика, свойства таких массивов могут значительно отличаться от свойств составляющих их компонент. Задачи о напряженно-деформированном состоянии неоднородной среды содержат дифференциальные уравнения с быстро меняющимися коэффициентами, которые характеризуют свойства отдельных компонент материала. Это серьезно усложняет решение данных краевых задач даже при использовании современных компьютеров, так как требует больших затрат машинного времени. Поэтому создаются модели, содержащие более простые уравнения с усредненными (эффективными) коэффициентами. Общая теория усреднения и примеры решения задач с применением этой теории даны, например, в работе [1]. Кроме того, подобные среды обладают способностью с течением времени медленно деформироваться при постоянных напряжениях, то есть обладают свойством ползучести [2, 3]. С помощью метода асимптотического усреднения в [4] построена математическая модель малых перемещений для комбинированной среды, состоящей из взаимно чередующихся слоев вязкоупругого материала и вязкой сжимаемой жидкости. Задача о прохождении плоской звуковой волны через композит конечной толщины со слоями упругого и вязкоупругого изотропных материалов решается в [5] также с использованием усредненной модели.
Работы [6, 7] иллюстрируют применение метода усреднения в задачах упругопластического изгиба пластин. Для гетерогенных сред, состоящих из упругого и вязкоупругого материалов [8], а также из двух ползучих материалов [9], построены соответствующие усредненные модели, описывающие совместное движение слоев. В работе [10] получены эффективные модули упругости слоистой упруго-ползучей среды.
Целью работы является моделирование напряженного состояния массива слоистых упругих пород, содержащего вертикальную шахту, с помощью теории усреднения, а при построении решения для массива из упруго-ползучих пород с помощью метода, основанного на комбинации теории усреднения и теории ползучести.
Методы решения. Использованы механические модели теории упругости и теории ползучести. В качестве основных реологических соотношений принимаются соотношения теории линейной наследственности Больцмана – Вольтерра
,
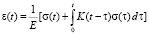где ε – деформация, t – время, E – модуль Юнга, σ – напряжение, K(t) – ядро ползучести, которое является убывающей функцией времени [2]. Параметры реологической модели определяются на основе лабораторных испытаний. Применение преобразования Лапласа сводит задачу для упруго-ползучего массива к задаче теории упругости с коэффициентами, зависящими от параметра. Кроме того, использовано имеющееся в литературе решение о напряженно-деформированном состоянии трансверсально-изотропного массива с вертикальной цилиндрической шахтой кругового поперечного сечения.
В статье рассматривается слоистый горный массив, ограниченный горизонтальной плоскостью. Изотропные слои, из которых он состоит, взаимно чередуются и расположены также горизонтально. В данном массиве имеется вертикальная полость в виде цилиндра кругового поперечного сечения радиуса R, идущая от граничной плоскости. Требуется определить напряжения в данном массиве в случае, когда объемная сила – это его вес.
Выберем цилиндрическую систему координат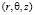 
с началом в центре верхнего кругового сечения полости и осью z, направленной вертикально вниз (рисунок).
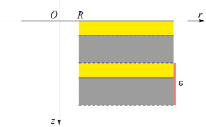
Сечение полуплоскостью Orz слоистого горного массива, содержащего вертикальную цилиндрическую полость кругового поперечного сечения радиуса R (ε – относительный период ячейки периодичности)
Массив, состоящий из чисто упругих слоев
Уравнения равновесия (1) и уравнения состояния (2) для каждого слоя, составляющего массив, имеют вид
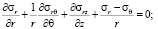
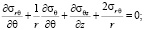(1)
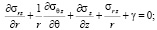
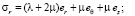
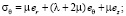
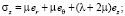(2)
,
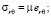
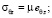
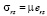где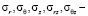 
компоненты напряжений, 
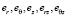– компоненты деформаций сплошной среды, λ, μ – постоянные Ламе, γ – величина удельного веса породы. Нагрузки на поверхности полости отсутствуют, то есть σr = 0 и σrz = 0 при r = R. На граничной поверхности z = 0 выполняются условия: σz = 0 и σrz = 0.
На горизонтальных граничных плоскостях слоев заданы условия идеального контакта: непрерывны все компоненты перемещений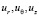 
и нормальная компонента напряжений σz, параллельная оси oz, то есть 
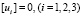и [σz] = 0.
Метод усреднения неоднородной упругой среды базируется на построении асимптотического решения по отношению к периоду составной среды [1]. Все модули упругости и удельный вес являются периодическими функциями координаты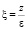 
(ε – относительный период ячейки) и кусочно-постоянными функциями этой переменной:
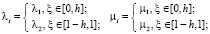
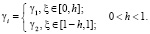(3)
После применения метода усреднения получаем однородный трансверсально-изотропный массив. Уравнения состояния такой среды можно записать в следующем виде [11]:
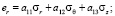
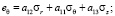
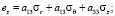
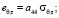
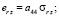
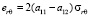, (4)
где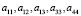 
– упругие податливости, являющиеся постоянными коэффициентами.
В работе [11] решена задача о распределении напряжений в массиве из трансверсально-изотропного материала с вертикальной цилиндрической полостью, имеющего плоскость изотропии, перпендикулярную оси z, получены следующие выражения для компонент напряжений (при условии, что uθ = 0 и, следовательно, τrθ = 0, τθz = 0):
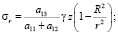
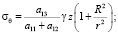
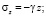
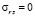. (5)
Подставим в (5) усредненные значения упругих податливостей а11, а12, а13, а33, а44, [12]. В результате получим
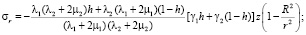
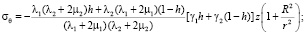(6)
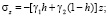
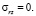
Напряжение σθ в радиальных сечениях у поверхности шахты:
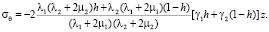
Это напряжение будет в два раза больше, чем в сплошном массиве без полости на таком же расстоянии z от горизонтальной плоскости, ограничивающей массив.
Если перемещения на поверхности шахты в радиальном направлении невозможны (например, когда боковая поверхность шахты закреплена трубой), то граничные условия на ней будут ur = 0 и σrz = 0 при r = R. В этом случае радиальное напряжение, оказываемое массивом на стенку трубы:
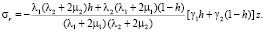
Если на поверхности шахты действует давление qz, меняющееся пропорционально расстоянию [11], то к напряжениям σr и σθ в формулах (6) добавятся соответственно
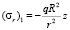и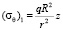 
.
Массив, состоящий из упруго-ползучих слоев
Пусть данный горный массив состоит из упруго-ползучих слоев, уравнения состояния для которых имеют вид
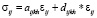, (i, j = 1, 2, 3). (7)
Здесь символ * обозначает оператор свертки:
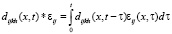. (8)
То, что ядра релаксации зависят от разности t – τ, как доказал Вольтерра, вытекает из условия инвариантности величин компонент тензора напряжений σij относительно изменений начала отсчета времени t.
Так как исходные слои упруго-ползучих материалов предполагаются изотропными, тензоры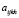 
и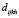 
(i, j, k, h = 1,2,3) в (7) соответственно имеют вид [2]:
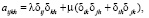(9)
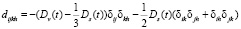. (10)
Здесь λ, μ – постоянные Ламе, δij – символ Кронекера, Ds(t) и Dν(t) – регулярные части ядер сдвиговой и объемной релаксаций соответственно. Предположим, что Dν(t) = kDs(t), где k = 0 или k = const > 1/3. Далее Ds(t) обозначим через D.
Пусть для каждого слоя ядро ползучести имеет вид: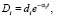 
где αi, di – постоянные, 
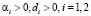, i – номер слоя, t – переменная, задающая время.
К уравнениям (7) с учетом (9), (10) применим преобразование Лапласа по времени:
.
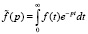В результате получим задачу теории упругости, в уравнениях которой все коэффициенты зависят от параметра p. К такой задаче применим метод усреднения [1]. Используя формулы (5) для компонент напряжений трансверсально-изотропного тела и выражения для усредненных (эффективных) модулей упругости, полученные в работе [12], запишем решение поставленной задачи в изображениях Лапласа:
;
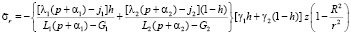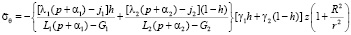; (11)
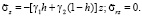
После применения к (11) обратного преобразования Лапласа формулы для компонент напряжений будут иметь вид
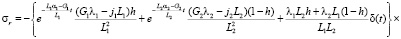
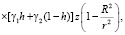(12)
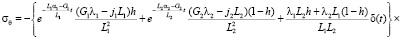
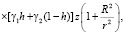(13)
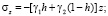
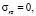
где δ(t) – дельта-функция Дирака. В этих формулах введены следующие обозначения
(i – номер слоя, i = 1,2):
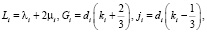
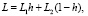
ki – коэффициенты пропорциональности ядер объемной релаксации ядрам сдвиговой для каждого слоя. Кроме того, p1, p2 – корни следующего квадратного уравнения:
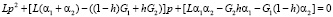, (14)
имеющего положительный дискриминант
.
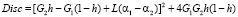Отсюда следует, что p1, p2 – действительные числа.
Напряжение σθ рядом с поверхностью круговой полости (r = R) для любых углов θ будет
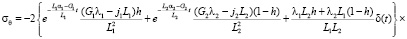
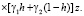
В случае, когда боковая поверхность шахты закреплена, например, трубой, шахта не оказывает влияния на напряжения, они будут такими же, как и в массиве без нее. На стенку трубы массив будет оказывать давление:
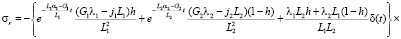
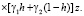
Если на поверхности шахты действует давление qz, меняющееся пропорционально расстоянию z (например, внутри находится жидкость [11]), то к напряжению σr в формуле (12) добавится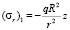 
, а к напряжению σθ в формуле (13) 
.
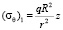Выводы
В работе применен метод усреднения, с помощью которого изучаются физические явления в неоднородных средах с периодической структурой. С помощью этого метода слоистый массив с вертикальной шахтой моделируется однородным трансверсально-изотропным полупространством с плоскостью изотропии, перпендикулярной вертикальной оси Oz. В результате получено распределение напряжений для различных граничных условий на поверхности шахты, когда между слоями выполнены условия идеального контакта. Рассмотрены два случая: изотропные чисто упругие слои и изотропные упруго-ползучие слои, для каждого из которых задано экспоненциальное ядро релаксации, зависящее от двух параметров. Эти параметры могут быть идентифицированы с помощью эксперимента.
Следует заметить, что использование в качестве ядер релаксации экспоненциальных ядер позволило в явном виде построить усредненную систему напряжений. Полученные в работе результаты могут быть весьма полезны для ряда прикладных задач.