Принцип аналитического гирокомпасирования широко применяется для определения ориентации неподвижных объектов по отношению к связанной с Землей горизонтальной, географически ориентированной системе координат, в частности, в инклинометрии скважин [1–3]. В общем случае в состав системы аналитического гирокомпасирования входят три датчика линейного ускорения (акселерометра), оси чувствительности которых направлены вдоль осей связанной с объектом системы координат, три гироскопических датчика угловой скорости (ДУС) с осями чувствительности, направленными параллельно тем же осям, и вычислитель. Если углы отклонения объекта по отношению к плоскости горизонта (вертикали места) ограничены, то возможен усечённый вариант системы, содержащий два акселерометра, два ДУС и вычислитель.
При использовании в системе акселерометров навигационного класса обеспечивается достаточно высокая точность определения параметров, характеризующих ориентацию объекта по отношению к плоскости горизонта. Проблемным является обеспечение необходимой точности определения ориентации объекта в азимуте. Для того, чтобы погрешность определения азимутального угла не превышала 1 ° на средних широтах, погрешности измерения ДУС не должны превышать десятых долей град/час. Для обеспечения погрешности определения азимутального угла на уровне 10 угловых минут погрешности ДУС не должны превышать сотых долей град/час. Для сравнения: тело, вращающееся вокруг оси с постоянной скоростью и делающее один оборот за год, вращается со скоростью 0,0416 град/час. Поэтому актуальной является разработка способов, приёмов и алгоритмов, позволяющих исключить либо уменьшить влияние погрешностей ДУС на точность определения азимутального угла.
Эффективным в этом отношении является метод, основанный на обработке результатов двух замеров каждым ДУС, у которых пространственное положение осей чувствительности изменяется на противоположное [4, 5]. В этом случае исключается влияние на результат гирокомпасирования смещения нулей ДУС и изменения их крутизны характеристики при условии, что в течение всего цикла измерения эти параметры остаются неизменными. Иногда этот метод называют методом двойного гирокомпасирования. Однако устройство для точной переориентации осей чувствительности ДУС делает прибор более сложным и дорогим.
Находит применение также метод, при котором один ДУС вращается с постоянной, достаточно малой скоростью вокруг вертикальной оси, в результате чего ось чувствительности ДУС непрерывно меняет свою ориентацию по отношению к вектору угловой скорости вращения Земли. Искомый угол, характеризующий ориентацию прибора в азимуте, определяется путём минимизации функции невязки между сигналом ДУС и вычисленным значением гармонической функции угла в определённые моменты времени. Такой метод определения азимута реализован в гироскопическом инклинометре ИГН73-100/80 [6]. Недостатком метода является необходимость выполнения большого объёма вычислений. Предлагаются также другие варианты определения направления на Север с помощью вращающегося вокруг вертикальной оси ДУС [7, 8].
Настоящая статья посвящена разработке приёмов и алгоритмов вычислений в системе аналитического гирокомпасирования, в которой используется один ДУС, установленный на платформе, вращающейся с постоянной скоростью. Причём жёстких требований к вертикализации прибора не предъявляется. Прибор может быть наклонён по отношению к вертикали места в любом направлении на угол до 15–20 градусов. Прибор входит в состав разрабатываемой системы ориентации и навигации горнопроходческого комбайна [9]. Составные части прибора и их положение относительно опорной и связанной с корпусом прибора системы координат показаны на рис. 1.
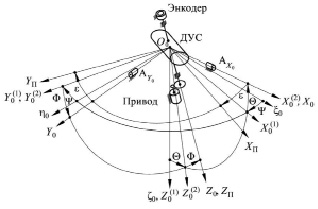
Рис. 1. Составные части прибора и их положение относительно опорной и связанной с корпусом прибора систем координат
На рис. 1 обозначено:
-О0ξ0η0ζ0 – горизонтальная, географически ориентированная, правая опорная система координат (СК), ось О0ζ0 которой направлена по вертикали вниз; оси О0ξ0 и О0η0 расположены в плоскости горизонта, причем ось О0ξ0 направлена на географический Север;
- О0X0Y0Z0 – правая СК, связанная с корпусом прибора; ось О0Z0 направлена вдоль оси вращения платформы в сторону нижней части прибора; оси О0X0 и О0Y0 лежат в экваториальной плоскости прибора;
- О0XПYПZП – правая СК, связанная с платформой; ось О0ZП совпадает с осью О0Z0; оси О0XП и О0YП в исходном положении совпадают с осями О0X0 и О0Y0 соответственно;
- Ψ, Θ, Φ – углы Эйлера – Крылова, характеризующие ориентацию СК О0X0Y0Z0 по отношению к СК 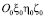 ; угол Ψ будем называть азимутальном углом прибора;
; угол Ψ будем называть азимутальном углом прибора;
- ε – угол поворота платформы вокруг оси О0ZП;
- 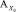 ,
, 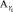 – акселерометры, установленные по осям О0X0 и О0Y0 соответственно.
– акселерометры, установленные по осям О0X0 и О0Y0 соответственно.
Принцип работы прибора
При вращении платформы с постоянной скоростью сигнал с ДУС изменяется по гармоническому закону в зависимости от угла ε, принимая нулевое значение дважды за один оборот. Определяются два первых последовательных угла (ε1, ε2), характеризующие положения платформы относительно корпуса в моменты времени, когда сигнал ДУС равен нулю. Вычисляется среднее арифметическое значение этих углов и таким образом находится угловое положение платформы, в котором ось чувствительности ДУС направлена либо на условный Север (εN), если в положении платформы, характеризующемся углом ε1, производная сигнала ДУС положительна, либо на условный Юг (εS), если в положении платформы, характеризующемся углом ε1, производная сигнала ДУС отрицательна (рис. 2).
Под условным Севером здесь понимается такое значение угла ε, при котором проекция вектора угловой скорости вращения Земли на ось чувствительности ДУС положительна и максимальна по модулю. Под условным Югом – значение угла ε, при котором проекция вектора угловой скорости вращения Земли на ось чувствительности ДУС отрицательна и максимальна по модулю. При строго вертикальном положении оси вращения платформы понятия «Север условный» и «Юг условный» совпадают соответственно с понятиями «Север» и «Юг» истинные. Зная угол εN (или εS) и ориентацию платформы относительно вертикали, можно определить азимутальный угол корпуса прибора. Ниже предлагается алгоритм вычисления угла Ψ по известным значениям углов εN, Θ и Φ. Алгоритмы вычисления углов Θ и Φ по информации с акселерометров здесь не рассматриваются. С ними можно ознакомиться, например, в [10].
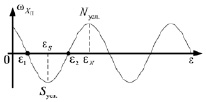
Рис. 2. График, поясняющий метод определения ориентации проекции вектора угловой скорости вращения Земли на экваториальную плоскость прибора Nусл. – условный Север; Sусл. – условный Юг
Вычисление угла Ψ по известным Θ, Φ, ε и φ0
Обозначим проекции вектора абсолютной угловой скорости вращения трёхгранника осей СК О0ξ0η0ζ0: 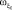 ,
, 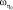 ,
, 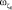 соответственно. Поскольку вращения трёхгранника происходят по причине вращения Земли с угловой скоростью
соответственно. Поскольку вращения трёхгранника происходят по причине вращения Земли с угловой скоростью 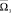 , то с учётом ориентации СК О0ξ0η0ζ0 относительно Земли имеем
, то с учётом ориентации СК О0ξ0η0ζ0 относительно Земли имеем
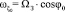 ;
; 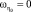 ;
; 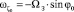 ,
,
где φ0 – широта местоположения прибора.
Найдём проекции вектора 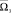 на ось О0XП. С этой целью сначала запишем выражения для проекций вектора
на ось О0XП. С этой целью сначала запишем выражения для проекций вектора 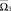 на оси СК О0X0Y0Z0:
на оси СК О0X0Y0Z0:
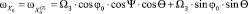 ;
;
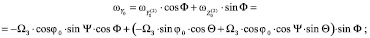
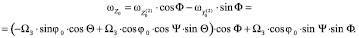
Искомая проекция вектора угловой скорости вращения Земли на ось чувствительности ДУС О0XП определится
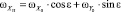 . (1)
. (1)
При ε = εN функция 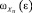 имеет экстремум и при этом положительна. Это позволяет записать следующие уравнение и неравенство:
имеет экстремум и при этом положительна. Это позволяет записать следующие уравнение и неравенство:
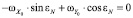 ; (2)
; (2)
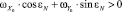 . (3)
. (3)
Поставив в уравнение (2) и неравенство (3) выражения для угловых скоростей 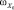 и
и 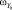 , получим
, получим
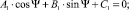 (4)
(4)
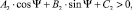 (5)
(5)
где
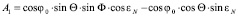 ;
;
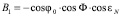 ;
;
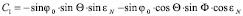 ;
;
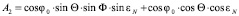 ;
;
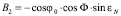 ;
;
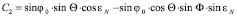 .
.
Уравнение (4) даже с учётом неравенства (5) не даёт однозначного решения для угла Ψ. Поступим следующим образом. Будем считать неизвестными в полученных уравнении и неравенстве значения sin Ψ и cos Ψ, добавив к этим уравнению и неравенству уравнение, связывающее между собой sin Ψ и cos Ψ
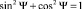 . (6)
. (6)
Выразим из (4) cos Ψ:
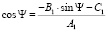 . (7)
. (7)
Подставив (7) в (6), получим квадратное уравнение относительно sin Ψ
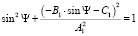 ,
,
которое можно записать в виде
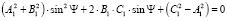 . (8)
. (8)
Дискриминант этого уравнения имеет вид
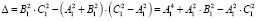 .
.
Если 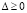 , то уравнение (8) имеет два решения. Первое решение будет
, то уравнение (8) имеет два решения. Первое решение будет
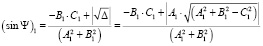 . (9)
. (9)
Подставив первое решение для sin Ψ в (7), получим
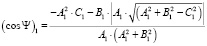 . (10)
. (10)
Тогда второе решение уравнения (8) будет иметь вид
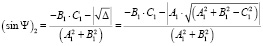 . (11)
. (11)
Соответственно, второе решение для cos Ψ будет иметь вид
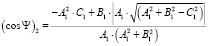 . (12)
. (12)
Из двух пар значений 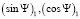 и
и 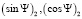 выберем ту, которая удовлетворяет неравенству (5). Эта полученная пара значений синуса и косинуса искомого угла позволяет определить его единственное значение. Главное значение угла вычисляется по формуле
выберем ту, которая удовлетворяет неравенству (5). Эта полученная пара значений синуса и косинуса искомого угла позволяет определить его единственное значение. Главное значение угла вычисляется по формуле
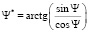 . (13)
. (13)
Здесь под главным значением понимается значение острого угла, который может быть как положительным, так и отрицательным. Действительное значение угла Ψ будет определяться с учётом квадранта, в котором лежит угол по известным формулам приведения. Квадрант определяется по знакам sin Ψ и sin Ψ. Алгоритм определения действительного значения угла Ψ представлен в виде табл. 1.
Таблица 1
Определение действительного значения угла Ψ
|
Квадрант, в котором лежит угол Ψ |
Действительное значение угла Ψ |
|
|
sin Ψ > 0, cos Ψ > 0 |
первый |
Ψ = Ψ* |
|
sin Ψ > 0, cos Ψ < 0 |
второй |
Ψ = Ψ* + 108 ° |
|
sin Ψ < 0, cos Ψ < 0 |
третий |
Ψ = Ψ* + 108 ° |
|
sin Ψ < 0, cos Ψ > 0 |
четвёртый |
Ψ = Ψ* + 360 ° |
Достоверность полученных алгоритмов подтверждена численными экспериментами.
Рассмотрим влияние основных погрешностей ДУС на точность определения угла εN .
Смещение нуля и изменение крутизны характеристики ДУС (чувствительности, масштаба) от пуска к пуску
Если указанные параметры остаются неизменными в пуске, то они не оказывают влияния на точность определения угла εN, а, следовательно, и угла Ψ. На рис. 3 показано изменение выходного сигнала ДУС в функции от угла Ψ при наличии смещения нуля и изменения чувствительности.
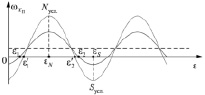
Рис. 3. Выходной сигнал ДУС при наличии смещения нуля и изменения крутизны его характеристики
Видно, что углы ε1 и ε2 при этом изменяются, но значение εN, как среднее арифметическое между ними, остаётся неизменным.
Фазовая погрешность ДУС
При измерении ДУС угловой скорости, изменяющейся по гармоническому закону, возникают известные динамические погрешности, которые относятся к категории методических и делятся на амплитудные и фазовые. При постоянной скорости вращения платформы эти погрешности постоянны. Выше показано, что изменение εN. Наличие фазовой погрешности (фазового сдвига) ДУС приводит к одинаковым погрешностям определения углов ε1 и ε2, следовательно, и угла εN.
Для ДУС, построенных на основе двухстепенного гироскопа с механическим упругим элементом, и компенсационного типа при условии безынерционности всех звенев, образующих цепь компенсации (цепь обратной связи), передаточная функция представляет собой передаточную функцию устойчивого колебательного звена. Сдвиг фазы такого звена определяется формулой [11]
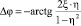 , (14)
, (14)
где Δφ – сдвиг фазы звена;
ξ – коэффициент затухания звена;
η – безразмерная частота, определяемая отношением круговой частоты изменения угловой скорости (скорости вращения платформы) к собственной частоте ДУС [12].
Величины сдвига фаз при различных значениях безразмерной частоты изменения угловой скорости η и близком к оптимальному значению коэффициента затухания ξ приведены в табл. 2.
Таблица 2
Результаты расчёта сдвига фаз по формуле (14)
|
п/п |
Коэффициент затухания звена ξ |
Безразмерная частота η |
Фазовая погрешность Δφ, угл. мин. |
|
1 |
0,6 |
0,000003 |
–0,012600 |
|
2 |
0,6 |
0,000030 |
–0,123600 |
|
3 |
0,6 |
0,000300 |
–12,37800 |
|
4 |
0,6 |
0,003000 |
–12,37620 |
|
5 |
0,6 |
0,030000 |
–123,8202 |
В ДУС, построенном на основе трёхстепенного гироскопа, в том числе на основе динамически настраиваемого гироскопа, в случае безынерционных цепей обратных связей, передаточная функция представляет собой передаточную функцию апериодического звена первого порядка. Фазовый сдвиг этого звена определяется формулой
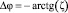 , (15)
, (15)
где η – безразмерная частота – отношение круговой частоты изменения угловой скорости к частоте изгиба асимптотической амплитудно-частотной характеристики звена.
Результаты расчёта сдвига фаз по формуле (15) представлены в табл. 3.
Таблица 3
Результаты расчёта сдвига фаз по формуле (15)
|
п/п |
Безразмерная частота ζ |
Фазовая погрешность Δφ, угл. мин. |
|
1 |
0,000003 |
–0,0103200 |
|
2 |
0,000030 |
–0,1031400 |
|
3 |
0,000300 |
–1,0313400 |
|
4 |
0,003000 |
–10,313520 |
|
5 |
0,030000 |
–103,10454 |
Из приведенных таблиц следует, что при определённых условиях величина ошибки в определении угла εN, вызванной фазовой погрешностью, может принимать недопустимо большие значения. Например, при скорости вращения платформы 10 град/с и собственной частоте колебаний ДУС на основе двухстепенного гироскопа, равной 10 Гц, при ξ = 0,6 имеем η = 0,00278, Δφ = 11,46 угл. мин.
Для исключения влияния фазовой погрешности ДУСа на результат определения угла εN предлагается после снятия отсчётов углов 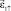 и
и 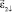 при вращении платформы в одну сторону изменить направление вращения на противоположное и снять отсчёты
при вращении платформы в одну сторону изменить направление вращения на противоположное и снять отсчёты 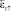 и
и 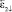 . В обозначениях углов ε1 и ε2 стрелки сверху означают направление вращения платформы (направление изменения угла ε). Стрелки после индекса означают знак производной при данном значении угла. Стрелка вверх – производная положительна, стрелка вниз – производная отрицательна.
. В обозначениях углов ε1 и ε2 стрелки сверху означают направление вращения платформы (направление изменения угла ε). Стрелки после индекса означают знак производной при данном значении угла. Стрелка вверх – производная положительна, стрелка вниз – производная отрицательна.
Для определения значения угла εN вычисляются значения углов 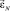 и
и 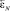 и находится среднее значение между ними.
и находится среднее значение между ними.
Устранение влияния фазовой погрешности в этом случае поясняется рис. 4.
На рис. 4 изображено:
- кривая 1 – график, отражающий изменение сигнала ДУС при отсутствии сдвига фаз;
- кривая 2 – график, отражающий изменение сигнала ДУС при вращении платформы в положительном направлении при наличии сдвига фаз;
- кривая 3 – график, отражающий изменение сигнала ДУС при вращении платформы в отрицательном направлении при наличии сдвига фаз.
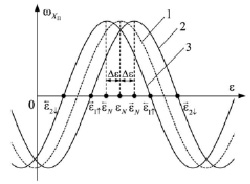
Рис. 4. К пояснению способа устранения влияния фазовой погрешности ДУС
При вращении платформы в положительном направлении будем иметь
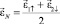 . (16)
. (16)
При вращении платформы в отрицательном направлении будем иметь
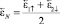 . (17)
. (17)
Вычислив среднее значение углов, определяемых выражениями (16) и (17), найдём
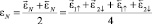 . (18)
. (18)
Значение εN, вычисляемое по формуле (18), не зависит от запаздывания, вносимого ДУС.
Запаздывание в определении угла ε по показаниям энкодера
В соответствии с принципом работы прибора с энкодера считывается код угла в тот момент времени, когда выходное напряжение ДУС с аналоговым выходом становится равным нулю. С этой целью используется компаратор, на первый вход которого подаётся напряжение с выхода ДУС, а на второй – напряжение, равное нулю. Выходной сигнал компаратора поступает в схему управления энкодера, в результате чего в вычислитель выдаётся тот код угла, который был на выходе энкодера на момент прихода сигнала с компаратора. Аналогично по сути всё происходит при использовании ДУС с цифровым выходом.
Однако в действительности за счёт наличия порога чувствительности компаратора и некоторой задержки выдачи кода схемой управления энкодера возникнет запаздывание. Если принять величину указанного запаздывания постоянной и не зависящей от направления вращения, то, очевидно, что при вычислении угла εN по формуле (18) это запаздывание на точность определения угла εN влияния также оказывать не будет.
Помехи (шум) в выходном сигнале ДУС
Реальный сигнал на выходе ДУС отличается от того, что изображён на рис. 3 и 4. Он содержит шум с широким частотным спектром. Характер спектра зависит от типа используемого ДУС, внешних механических воздействий на ДУС в процессе измерений, а также характера и уровня внутренних и внешних наводок на электронную часть прибора [13]. Например, в ДУС на основе роторных гироскопов присутствие сравнительно низкочастотных гармоник помех в выходном сигнале обусловлено воздействием на прибор внешних вибраций и ударов, шумом, создаваемым шарикоподшипниками подвеса ротора, дисбалансом последнего и другими дефектами механической части ДУС. Высокочастотные гармоники, как правило, обусловлены помехами электрического происхождения, возникающими в электронной части ДУС, а также внешними наводками.
Наличие помех в выходном сигнале ДУС приведёт к разбросу моментов срабатывания компаратора относительно момента равенства нулю сигнала ДУС при отсутствии помех. Возникает погрешность Δε, которая может быть как положительной, так и отрицательной. Возникновение погрешности Δε при наличии в выходном сигнале ДУС одной высокочастотной гармонической составляющей помехи показано на рис. 5.
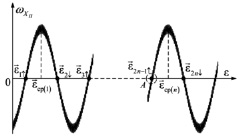
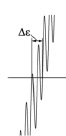
а) б)
Рис. 5. График, отражающий изменение выходного сигнала ДУС при наличии помехи (а) и этот же график в увеличенном масштабе для диапазона угла ε вблизи точки А (б)
Если принять, что погрешность Δε является случайной величиной с нормальным законом распределения относительно нулевого значения, то для снижения влияния этого фактора на точность определения угла εN можно рекомендовать следующий приём. Наблюдения и вычисления ведутся в течение промежутка времени, за который платформа делает n оборотов в одну и n оборотов в другую сторону. При этом угол 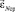 вычисляется как среднее между углами
вычисляется как среднее между углами 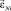
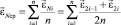 , (19)
, (19)
где n – число пар отсчётов (число оборотов платформы).
И угол 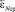 вычисляется как среднее между углами
вычисляется как среднее между углами 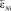
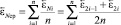 . (20)
. (20)
Проведённый анализ позволяет записать итоговую формулу, вычисление по которой угла εN обеспечит наибольшую точность
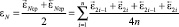 . (21)
. (21)
Влияние шума в выходном сигнале ДУС на точность определения азимутального угла будет снижаться по мере увеличения числа n, а это напрямую связано со временем определения азимутального угла.
Последовательность действий по определению углов Ψ, Θ, Φ
Приведём последовательность действий по определению углов Эйлера – Крылова Ψ, Θ, Φ, характеризующих ориентацию прибора по отношению к горизонтальной, географически ориентированной системе координат.
1. В вычислитель вводится значение широты места φ0, а также значение ускорения силы тяжести на экваторе g0.
2. Вычисляется величина ускорения силы тяжести g места [14].
3. Вычисляются углы Θ и Φ по сигналам с акселерометров с учётом найденного значения ускорения силы тяжести.
4. Платформа приводится во вращение в положительном направлении и с энкодера снимаются и записываются в память вычислителя отсчёты 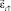 и
и 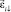 в течение промежутка времени, необходимого для снятия n пар отсчётов.
в течение промежутка времени, необходимого для снятия n пар отсчётов.
5. Меняется направление вращения платформы на противоположное, снимаются и записываются в память вычислителя n пар отсчётов 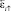 и
и 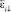 .
.
6. Вычисляется значение угла εN по формуле (21).
7. Вычисляются значения 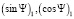 и
и 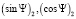 по формулам (9–12).
по формулам (9–12).
8. Определяется пара значений sin Ψ и cos Ψ, которая удовлетворяет неравенству (5).
9. Вычисляется главное значение угла Ψ по формуле (13).
10. Определяется действительное значение угла Ψ с использованием алгоритмов, представленных в табл. 1.
Заключение
Предложенные структура наземного прибора ориентации, приемы измерения и алгоритмы вычисления параметров его ориентации позволяют исключить влияние смещения нуля датчика угловой скорости, изменения крутизны его характеристики и фазовой погрешности на точность определения азимутального угла при условии, что в течение всего цикла измерения указанные параметры остаются постоянными. Кроме того, они позволяют уменьшить влияние шума в выходном сигнале датчика на точность определения этого угла.



