Потребности решения прикладных задач в реальном масштабе времени обуславливают интерес к разработке методов оптимизации с гарантийными оценками трудоемкости вычислений, а также к поиску возможностей повышения эффективности известных методов путем их модификации [1].
Применительно к задачам линейного программирования (ЛП) в качестве первой успешной попытки решения проблемы можно рассматривать результаты работы [2], распространенные в дальнейшем на некоторые классы задач нелинейного программирования. Несмотря на это, методы симплексного типа (МСТ) остаются по-прежнему основными для решения задач ЛП [3, 4], благодаря их более высокой статистической эффективности практически на всем многообразии прикладных задач, хотя и известны «искусственные» примеры, когда применение МСТ равносильно полному перебору опорных планов задачи [5, 6].
По-видимому, в связи с этим в теории и практике решения задач математического программирования относительно мало уделяется внимания исследованию вычислительной сложности решения задач ЛП другими методами.
В частности, еще в [7] отмечалось, что метод проекции градиента (МПГ) часто требует для решения задачи ЛП меньшего числа итераций по сравнению с МСТ. Интуитивно высокая эффективность МПГ объясняется тем, что при его реализации переход между точками на очередной итерации может осуществляться по внутренней части многогранника допустимых решений или по его граням, в то время как при МСТ переходы всегда происходят по ребру многогранника.
Однако в известных алгоритмах МПГ эти потенциальные возможности реализованы не полностью. Основной их недостаток состоит в том, что размерность пространства (граней), в котором осуществляется движение, на каждой итерации уменьшается на единицу до получения опорного плана задачи ЛП. Далее вычислительный процесс становится эквивалентным использованию двойственного симплекс-метода [8]. Это приводит в результате к таким же сложностям получения оценок эффективности МПГ, как и при рассмотрении МСТ.
Целью настоящей работы является обоснование модификации МПГ, эквивалентной методу наискорейшего спуска, и дальнейшей модификации с целью ускорения сходимости модифицированного метода к решению задачи ЛП.
Модифицированный метод проекции градиента
Задачу ЛП в Rn без нарушения общности рассмотрения можно представить в следующем виде:
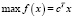(1)
при ограничениях
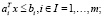
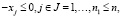(2)
где Rn – n-мерное арифметическое пространство, f(x) – целевая функция; с – матрица коэффициентов ai и bi; x – матрица переменных.
Будем считать, что условия (2) линейно независимы.
Для приведения к такому виду общей задачи ЛП с линейно-независимыми условиями вида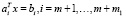 
достаточно разрешить эту систему уравнений относительно любых m1 переменных и исключить их из системы условий (2).
Для решения задачи ЛП методом ПГ на каждой итерации определяется [9, 10]: Nk (mk*n) – матрица, образованная транспонированными векторами-градиентами ограничений, которые по предположению на протяжении k-й итерации являются существенными, то есть выполняются как строгие равенства; Rk (n*n) – матрица проектирования; rk – n-вектор направления движения; δk – mk-вектор двойственных переменных, соответствующих существенным ограничениям.
При этом имеют место следующие соотношения
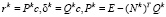, (3)
где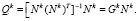 
Вычисления начинаются с допустимого решения системы (2) x0.
Значение вектора переменных после выполнения k итераций определяется выражением
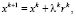(4)
где λk ≥ 0 – величина максимально допустимого шага в направлении rk.
Условия оптимальности решения xk имеют вид
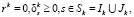(5)
где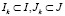 
– соответственно множества индексов существенных ограничений на k-й итерации.
В классической процедуре МПГ анализ существенности ограничений производится только в том случае, когда выполняется первое из необходимых условий оптимальности (5). При этом если xk не оптимально, одно из ограничений, для которого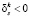 
переводится в несущественные (из матрицы Nk исключается строка) [11]. Затем осуществляется k + 1-я итерация.
Суть предлагаемой модификации МПГ состоит в том, что для перехода от xk к xk+1 определяется наилучшее из возможных направление движения по границе множества допустимых решений сокращенной задачи, которое далее используется для определения допустимого направления движения.
Один из возможных алгоритмов реализации модификации МПГ состоит из последовательности итераций, на каждой из которых (k ≥ 0) необходимо:
1) определить λk и xk+1;
2) сформировать Nk+1 путем присоединения к матрице Nk строки lT, соответствующей вектору градиента ограничения, определяющего λk, определить rk+1, δk+1;
3) проверить выполнение условий оптимальности.
Из матрицы Nk+1 последовательно исключить все строки, соответствующие несущественным ограничениям, для которых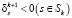 
, и скорректировать значения rk+1, δk+1, перейти к п.1.
Обоснование алгоритма модификации МПГ
Исследуем две вспомогательные задачи оптимизации, решение которых определяют направление движения: наилучшее в градиентных методах (задача А) и в методе ПГ (задача Б).
Задача А имеет вид [10]
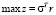(6)
при ограничениях
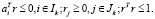(7)
Задача Б отличается от задачи А только характером ограничений, которые имеют вид:
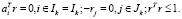(8)
Если задача Б разрешима, то ее решение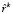 
может быть найдено по алгоритму МПГ. При этом выполнение последнего из условий (8) обеспечивается нормировкой (путем деления 
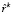на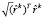 
). Оптимальность 
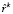для задачи Б следует непосредственно из определения проекции вектора на множество.
Понятно, что решения задач А и Б отличаются в том случае, когда среди ограничени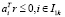й 
и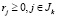 
есть несущественные для выбора наилучшего направления. Обозначим 
.
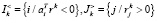По теореме Куна – Таккера необходимые и достаточные условия оптимальности решения r задач А и Б состоят в существовании векторов (α, αr) и rs ≥ 0 таких, что [10]:
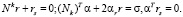(9)
При этом для задачи Б первое условие имеет вид Nkrk = 0, а последнее удовлетворяется при любых α, так как rs = 0.
Учитывая выражения для Pk и δk, легко видеть, что переменные α = δk удовлетворяют второму условию из (9) при αr = 0,5. Следовательно, δk являются множителями Лагранжа для задачи Б.
Представим линейные ограничения (8) в виде Nkr = β.
Известно, что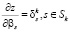 
.
Отсюда следует, что уменьшение любого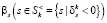 
приводит к увеличению значения целевой функции. Поэтому соответствующее ограничение является несущественным и его закрепление может быть снято. Исключив его из системы (8), приходим к задаче Б меньшей размерности.
Если имеются другие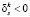 
, процесс исключения может быть повторен. В результате получим задачу Б для которой все 
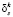неотрицательны. Решение последней задачи совпадает с решением задачи А.
В противоположном случае среди ограничений (8) должно найтись ограничение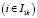 
или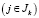 
, которое в задаче А несущественно. То есть, по крайней мере, для одного из этих ограничений должно быть 
.
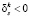Геометрически увеличение значения целевой функции в задаче Б или А означает увеличение значения косинуса угла между вектором-градиентом целевой функции и направлением движения, определяемым текущим решением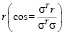 
и, следовательно, увеличение длины проекции вектора-градиента целевой функции на множество допустимых решений в задаче Б.
В силу единственности проекции вектора на множество – наилучшее направление также единственно. Следовательно, процесс исключения несущественных ограничений приводит к одной и той же задаче независимо от порядка их рассмотрения. При этом процесс может быть начат с любого ограничения, для которого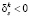 
. Отсюда следует, что все такие ограничения могут быть исключены одновременно.
Таким образом, МПГ при изменении правила выбора проектирующей матрицы на очередной итерации позволяет определить наилучшее направление движения по границе множества допустимых решений, которое совпадает с направлением наискорейшего спуска.
Определение эффективных допустимых направлений по данным модифицированного МПГ
Эффективность модифицированного МПГ в значительной степени определяется структурой множества допустимых решений и прежде всего количеством ограничений (2), которые могут оказаться существенными при реализации МПГ. Сокращение количества исследуемых гиперплоскостей может быть достигнуто при использовании полученных результатов для построения допустимых направлений движения во внутренней области МДР (максимально достижимым кодовым расстоянием) [12], которые приводят на каждом шаге к возможно наибольшему приращению целевой функции.
Пусть выполнено k итераций с использованием таких допустимых направлений и определено множество X = {xs|s = 0,…, k}.
На (k + 1)-й итерации очередная точка определяется в виде
,
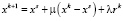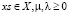. (10)
Очевидно, найдутся такие значения m, l, что xk + 1, определяемое таким образом, является допустимой точкой. В частности, при m = 1, l = lk получаем точку, соответствующую МПГ.
Для определения направления, приводящего к наибольшему приращению целевой функции, рассмотрим задачу
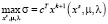(11)
при ограничениях
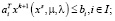
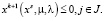
Возможны два случая решения этой задачи.
В первом случае m* = 1, l* = lk. Это означает, что нельзя найти допустимое направление выбранного вида, приводящее к большему значению целевой функции по сравнению с модифицированным МПГ. При этом выделяется одно новое существенное ограничение.
Во втором случае m* < 1, l* > lk. При этом выделяются два новых существенных ограничения.
Пусть при m = 1, l = lk существенным становится ограничение с номером q. Тогда для всех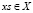 
имеем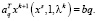 
Обозначим l = 1 – e, m = lk + d. Очевидно существуют такие e, d > 0, что имеет место
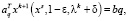
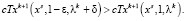
Для таких e, d получаем
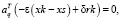
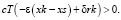
Исключая из равенства одну из переменных e, d и подставляя ее значение в неравенство, получаем, что при фиксированных значениях e, d наибольшее приращение целевой функции при движении в q-й гиперплоскости достигается тогда, когда
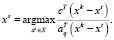
Выбор такого направления обеспечивает наилучшее приближение к направлению движения в q-й гиперплоскости при использовании модифицированного МПГ и поэтому может считаться наиболее целесообразным.
Задача (11) при фиксированном xs сводится к задаче линейного программирования с двумя переменными. Ее решение вычислительных трудностей не представляет.
Решение исходной задачи сводится, таким образом, к решению последовательности задач вида (11).
При этом, если m* = 1 определение rk и проверка условий оптимальности осуществляются по алгоритму модифицированного МПГ. При m* < 1 матрица Nk+1 формируется по двум ограничениям, определяющим решение задачи (11) и выражения (3) для определения rk, δk можно записать в явном виде.
Заключение
Сопоставление детального анализа оценок вычислительной сложности отдельных итераций и результатов многократной практической апробации алгоритма, реализующего предложенный подход, показывает, что незначительное увеличение вычислительной сложности, связанное с решением на каждой итерации задачи вида (11), компенсируется существенным уменьшением общего количества итераций по сравнению с алгоритмом МПГ. Предложенная схема формирования допустимых направлений не претендует на получение безупречно точного наиболее эффективного метода, а является только примером возможного синтеза методов градиентного спуска и симплексного типа в линейном программировании.