Задача формирования расписания экзаменов является задачей комбинаторной оптимизации, а по своей сложности относится к классу NP-полных задач. Последнее требует для своего решения применения таких эвристических методов, как раскраска графа [1, 2], поиск с запретами [3–5], алгоритмы муравьиных колоний [6], метод «великого» потопа [7], эволюционные алгоритмы [8] и другие [9, 10]. Наиболее близким к предлагаемому в статье способу решения задачи представляется многокритериальный подход [11].
Для решения задачи предлагаются две последовательно применяемые ресурсо-ориентированные эвристики, основанные на оценках загруженности и равномерности. Каждая эвристика является схемой формирования расписаний с правилами приоритетов [12]. Приоритетами являются многокритериальные критерии загруженности и равномерности для определения очередности конкурирующих по ресурсам заявок или экзаменов расписания. В основе правил приоритетов находятся методы ранжирования теории принятия решений.
Целью данной статьи является представление эвристик в программном решении задачи формирования расписания экзаменов российского вуза.
Аналогично задаче расписания занятий [13] расписание экзаменов связано с распределением трех ресурсов – студенческого контингента, преподавателей и аудиторий. Исходными данными являются формируемые для всех экзаменов сессии заявки с указанием группы, преподавателя и требуемой или желаемой аудитории. Для решения задачи использованы конструктивная эвристика формирования начального расписания SGS1 и оптимизационная эвристика SGS2.
Введем необходимые в математическом моделировании обозначения.
Исходные данные задачи:
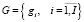 ,
, 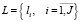 ,
, 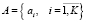 – множества академических групп, преподавателей и аудиторий;
– множества академических групп, преподавателей и аудиторий;
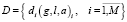 – множество заявок на прием экзаменов;
– множество заявок на прием экзаменов;
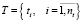 – множество таймслотов – временных интервалов приема экзаменов, однозначно определяющих номер смены – tn, день недели – td и ее номер – ts.
– множество таймслотов – временных интервалов приема экзаменов, однозначно определяющих номер смены – tn, день недели – td и ее номер – ts.
«Классическая» организация экзаменационной сессии предполагает ее трехнедельную продолжительность с двумя сменами в день, включая воскресенье. В этом случае 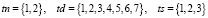 , а nt = 42.
, а nt = 42.
Исходные расчетные данные задачи:
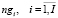 ,
, 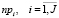 ,
, 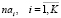 – количества заявок i-й группы, i-го преподавателя и i-й аудитории;
– количества заявок i-й группы, i-го преподавателя и i-й аудитории;
Переменные задачи:
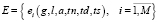 – множество экзаменов расписания;
– множество экзаменов расписания;
ni, nr – количества включенных и не включенных в начальное расписание экзаменов;
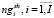 ,
, 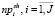 ,
, 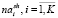 – количества включенных в начальное расписание экзаменов i-й группы, i-го преподавателя или i-й аудитории;
– количества включенных в начальное расписание экзаменов i-й группы, i-го преподавателя или i-й аудитории;
Таблица 1
Оценки загруженности заявок на прием экзаменов
|
i-й группы |
i-го преподавателя |
i-й аудитории |
|
|
|
|
wi – количество экзаменов в таймслоте ti интервала расписания сессии;
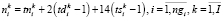 – номер таймслота проведения i-го экзамена k-й группы при «классической» организации экзаменационной сессии;
– номер таймслота проведения i-го экзамена k-й группы при «классической» организации экзаменационной сессии;
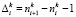 – интервал в таймслотах между i-м и (i + 1)-м экзаменами k-й группы. Для последнего экзамена группы (i + 1)-м экзаменом принимается первый экзамен с увеличением его номера на величину nt.
– интервал в таймслотах между i-м и (i + 1)-м экзаменами k-й группы. Для последнего экзамена группы (i + 1)-м экзаменом принимается первый экзамен с увеличением его номера на величину nt.
Для экзаменационной сессии использовано круговое представление (рис. 1), когнитивность [14] которого позволила ввести две оценки равномерности расписания экзаменов.
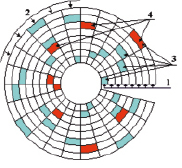
Рис. 1. Круговое представление экзаменационной сессии: 1 – кольцевые расписания экзаменов групп; 2 – таймслоты расписания; 3 – экзамены групп; 4 – первые включенные в расписание экзамены групп
Кольцевая оценка равномерности определяет распределение экзаменов группы в своем кольце представления. Радиальная оценка равномерности определяет распределение экзаменов в таймслотах представления. Выражения для определения кольцевых и радиальных оценок равномерности представлены в табл. 2.
Таблица 2
Оценки равномерности экзаменов
|
k-й группы |
i-го таймслота |
|
|
|
Критерий равномерности i-го экзамена расписания k-й группы
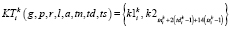 . (6)
. (6)
Критерии равномерности расписания экзаменов определяются двумя среднеквадратичными отклонениями (табл. 3).
Таблица 3
Критерии равномерности
|
расписания группы |
расписания |
|
|
|
Введем булевы обозначения занятости группы qg, преподавателя ql и аудитории qa.



Эвристика SGS1 (формирование начального расписания экзаменов) состоит в цикличном выборе наиболее загруженной заявки и ее включении в расписание так, чтобы минимизировать критерий равномерности группы включаемого экзамена
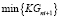 (9)
(9)
при обязательных ограничениях
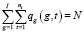 , (10)
, (10)
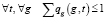 ,
, 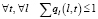 ,
, 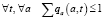 , (11)
, (11)
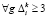 . (12)
. (12)
Целевая функция (9) обеспечивает наибольшую возможную равномерность экзаменов группы последней заявки. Ограничение (10) гарантирует включение всех заявок в начальное расписание. Неравенства ограничений (11) исключают возможность одновременного участия любой группы, преподавателя или аудитории более чем в одном экзамене расписания. Ограничение (12) обеспечивает необходимый интервал между ближайшими экзаменами любой группы в начальном расписании при «классической» организации экзаменационной сессии.
Каждый цикл эвристики SGS1 начинается перерасчетом оценок загруженности ресурсов (1–3), формирующих множество критериев загруженности заявок, не включенных в начальное расписание экзаменов.
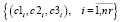 . (13)
. (13)
Обратное многокритериальное ранжирование [15] векторов (13) определяет самую загруженную заявку, которая становится очередным кандидатом dni+1 на включение в начальное расписание. Далее в эвристике SGS1 реализуются следующие действия. Если включаемый в начальное расписание экзамен является первым для группы, то он включается в первый таймслот с минимальным количеством экзаменов и для группы фиксируется множество таймслотов сессии (рис. 2) для размещения остальных экзаменов группы. Выделение этого множества осуществляется на основе ограничения (12). Если экзамен не первый, то из множества выделенных таймслотов выбирается первый с наименьшим значением оценки ki.
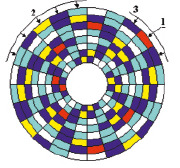
Рис. 2. Диапазоны допустимых таймслотов: 1 – первый включенный в расписание экзамен группы; 2 – допустимые таймслоты для начального расписания; 3 – допустимые таймслоты для оптимизации расписания
Если nr > 0, то переход к следующему циклу конструктивной эвристики. На рис. 3 представлено начальное расписание экзаменов для 50 групп, студенты которых сдают по 5 экзаменов. Программное решение реализовано для «классической» организации экзаменационной сессии. По периметру кругового представления (рис. 3) указаны количества программно определенных экзаменов в каждом таймслоте начального расписания. Критерий равномерности полученного расписания составляет KS = 26,93 %.
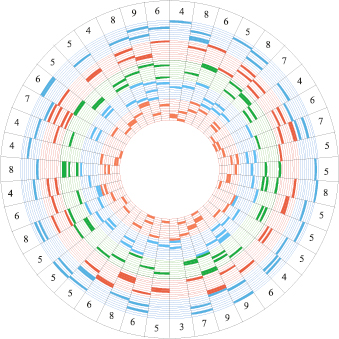
Рис. 3. Начальное расписание экзаменов
Эвристика SGS2 (оптимизация расписания экзаменов) состоит в цикличном выборе наиболее неравномерного экзамена и изменении расписания 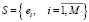 для минимизации критерия равномерности расписания (8) при обязательных ограничениях (10, 11) и уточнении ограничения (12).
для минимизации критерия равномерности расписания (8) при обязательных ограничениях (10, 11) и уточнении ограничения (12).
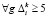 . (14)
. (14)
Каждый цикл оптимизации начинается переопределением оценок равномерности (4, 5) и формированием множеств первых и вторых оценок равномерности экзаменов расписания.
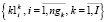 , (15)
, (15)
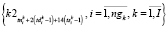 . (16)
. (16)
Многовекторным ранжированием [15] определяется самый неравномерный экзамен расписания следующим образом. Ранги, получаемые многокритериальным ранжированием векторов (15, 16), формируют множество векторов рангов:
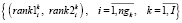 . (17)
. (17)
Многокритериальное ранжирование векторов (17) определяет самый неравномерный экзамен, становящийся очередным кандидатом на перестановку в расписании. Далее, как и в эвристике SGS1 определяется таймслот для перестановки. Работа эвристики SGS2 завершается при невозможности дальнейшего улучшения расписания экзаменационной сессии. На рис. 4 представлен один из вариантов оптимального расписания экзаменов. Критерий равномерности расписания составляет KS = 3,58 %, что существенно меньше аналогичного критерия начального расписания. Следует также отметить уменьшение количества аудиторий, требуемых для приема экзаменов.
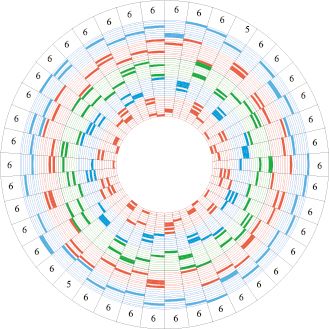
Рис. 4. Оптимальное расписание экзаменов
Заключение
Авторы считают что:
– разработан подход к формированию расписания экзаменов вуза с использованием двух последовательно применяемых эвристик;
– приведенная модель для «классической» организации экзаменационной сессии может быть трансформирована для других типов организации сессии.




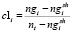 (1)
(1)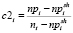 (2)
(2)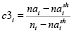 (3)
(3)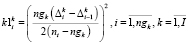 (4)
(4)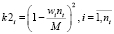 (5)
(5)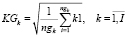 (7)
(7)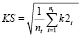 (8)
(8)