В настоящее время мобильные устройства широко используются в различных областях логистики, технического обслуживания и производства. Ключевые возможности геоинформационных систем (ГИС) в данных сферах позволяют выполнять мониторинг перемещений и координировать действия полевых сотрудников, что тесно связано со сбором, обработкой и хранением геоданных, поступающих с мобильных устройств [1–3]. Важность и актуальность задач обработки геолокационной информации обусловлена высокими требованиями к геоинформационным системам в различных областях применения [4–6].
Стратегия разделения ответственности по обработке геоинформации в ГИС, когда приоритет отдается мобильным приложениям, является предпочтительной. В этом случае существенно снижается нагрузка на серверную часть и уменьшается объем передаваемых данных, что в случае плохого соединения с сетью или полного отсутствия связи является ключевым фактором. Такая стратегия позволяет реализовать потоковую обработку данных в реальном времени на мобильном устройстве, что даст возможность получить высокоточные данные местоположения настолько быстро, насколько это возможно. Это, несомненно, важно для ГИС, которые предполагают немедленное реагирование на различные ситуации на основе данных местоположения.
Модели и методы фильтрации геоданных зачастую основаны на обработке информации в реальном времени [1, 2]. Их проектирование и разработка, а также экспериментальная оценка эффективности представляют собой нетривиальную задачу [7, 8]. Для оценки качества фильтрации обычно используют такую характеристику, как функцию ошибки, которую конструируют исходя из оценки идентичности целевой функции (целевого, реального маршрута, Ground Truth) и предсказаний классификатора или траектории движения на выходе фильтрации, учитывая специфику предметной области, таким образом, чтобы ошибка была максимально достоверной для данной конкретной задачи [9–11]. Значение функции ошибки должно уменьшаться с увеличением качества работы модели. При этом решая задачу минимизации функции, возможно найти оптимальные параметры модели. В качестве функции ошибки наряду с евклидовой метрикой часто используют кросс-энтропию или функцию потерь Хьюбера.
Определение функции ошибки
Рассматривая задачу фильтрации геокоординат, целевой маршрут можно представить в виде ломаной линии, заданной вектором кортежей. Каждый кортеж состоит из набора параметров: времени, широты и долготы, которые определяют точку в трехмерном пространстве:
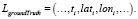 (1)
(1)
Траектория движения, полученная после фильтрации, также представляет собой ломаную:
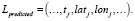 (2)
(2)
Особенностью такого представления является то, что количество элементов в векторах LgroundTruth и Lpredicted в общем случае может быть разным. Координаты широты lati(latj) и долготы loni(lonj) могут быть также разными в обеих ломаных. Только по параметру ti(tj) возможно однозначно определить две точки, соответствующие одному и тому же времени. По этому параметру существует некая неравномерная дискретизация координат: каждой единице времени tk соответствует не менее одного кортежа 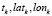 в векторах LgroundTruth и Lpredicted. То есть возможны случаи, когда:
в векторах LgroundTruth и Lpredicted. То есть возможны случаи, когда:
- 
- 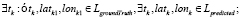
- 
Задача оценки качества фильтрации сводится к сравнению идентичности двух ломаных LgroundTruth и Lpredicted функцией ошибки 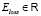 как по пространственным координатам lati и loni, так и по временным ti. Чем больше различаются ломаные, тем больше должно быть значение ошибки Eloss и наоборот. В общем случае
как по пространственным координатам lati и loni, так и по временным ti. Чем больше различаются ломаные, тем больше должно быть значение ошибки Eloss и наоборот. В общем случае 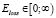 . При этом известно, что ломаные изначально так расположены в пространстве, что Eloss = min, так как всегда рассматривается одна и та же реальная траектория движения. Вектор Lpredicted в случае идеальной фильтрации должен совпадать с LgroundTruth, и Eloss = 0.
. При этом известно, что ломаные изначально так расположены в пространстве, что Eloss = min, так как всегда рассматривается одна и та же реальная траектория движения. Вектор Lpredicted в случае идеальной фильтрации должен совпадать с LgroundTruth, и Eloss = 0.
Идентичность ломаных в данном контексте следует понимать как степень соответствия каждой точки Lpredicted с соответствующей точкой в LgroundTruth. Степень подобия в отличие от идентичности не будет адекватной оценкой, поскольку ломаные могут быть схожи с высоким показателем подобия, однако расположены далеко друг от друга, при этом значение ошибки будет мало, что неверно.
Задача конструирования Eloss усложняется тем, что координаты точек на ломаных lati, loni и latj, lonj – это геокоординаты в замкнутом пространстве, эллипсоиде, а не точки на плоскости. Расстояние от точки до прямой здесь определяется дугой. Перевод геокоординат в прямоугольную систему координат может добавить существенную погрешность определения значения функции ошибки.
Конструирование функции ошибки
Рассмотрим возможные решения задачи нахождения максимально достоверной функции Eloss.
1. Ковариационный анализ. Метод предполагает составление матрицы ковариации между распределенными величинами, которые являются координатами точек на двух ломаных Lpredicted и LgroundTruth. После составления матрицы анализируются коэффициенты корреляции. По их значениям возможно определить степень идентичности двух ломаных, однако метод применим только в случае одинаковой дискретизации точек на ломаных, что в данном случае неверно.
2. Анализ Фурье и сравнение спектров. Проблема здесь аналогична п. 1. Для ее разрешения возможно аппроксимировать дискретные функции 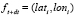 на интервалах времени t + dt непрерывными функциями для каждой ломаной, выполнить передискретизацию по времени и сравнить непрерывные функции ковариационным анализом, анализом Фурье или простым вычислением интеграла разницы функций на интервалах t + dt. Однако определение значения dt для максимально достоверной оценки представляет собой нетривиальную задачу. Дело в том, что ломаные могут описывать окружности на больших интервалах времени, и в таком случае аппроксимация не имеет смысла. На малых интервалах возможна большая погрешность вычисления ошибки Eloss.
на интервалах времени t + dt непрерывными функциями для каждой ломаной, выполнить передискретизацию по времени и сравнить непрерывные функции ковариационным анализом, анализом Фурье или простым вычислением интеграла разницы функций на интервалах t + dt. Однако определение значения dt для максимально достоверной оценки представляет собой нетривиальную задачу. Дело в том, что ломаные могут описывать окружности на больших интервалах времени, и в таком случае аппроксимация не имеет смысла. На малых интервалах возможна большая погрешность вычисления ошибки Eloss.
Предложим три подхода, основанные на векторном представлении ломаных. Первый определяет Eloss как разницу сумм изменения углов направления по двум ломаным. Второй подход заключается в сдвиге всех векторов в начало координат и подсчете разницы общих площадей под двумя ломаными. Однако в обоих случаях оценка может быть недостоверна, так как возможно построить два различных трека с нулевой ошибкой Eloss. Третий подход предполагает попарное сравнение векторов, но здесь появляется проблема дискретизации.
Все рассмотренные подходы с высокой степенью недостоверности вычисляют ошибку Eloss. Для декомпозиции задачи попробуем выделить частные случаи анализа двух ломаных. Допустим, моменту времени tk соответствуют две точки на обеих ломаных, то есть:
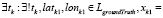
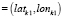
и 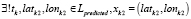 .
.
Ошибка здесь очевидно пропорциональна расстоянию между двумя точками 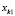 и
и 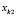 в метрах:
в метрах:
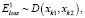 (3)
(3)
где D – функция расстояния между точками 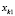 и
и 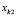 .
.
Рассмотрим второй случай, когда
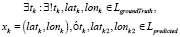
или
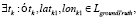
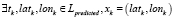 ,
,
то есть для момента времени tk существует только одна точка на одной из ломаных. Выполнение любого из условий сводится к одной и той же задаче, поэтому далее будем рассматривать точку 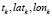 на одной ломаной (LgroundTruth или Lpredicted), для которой нет соответствующей точки на другой ломаной (Lpredicted или LgroundTruth). Ошибка здесь пропорциональна расстоянию от точки xk на первой ломаной до точки на второй ломаной
на одной ломаной (LgroundTruth или Lpredicted), для которой нет соответствующей точки на другой ломаной (Lpredicted или LgroundTruth). Ошибка здесь пропорциональна расстоянию от точки xk на первой ломаной до точки на второй ломаной 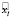 в метрах, которая на самом деле отсутствует:
в метрах, которая на самом деле отсутствует:
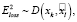 (4)
(4)
Эту точку целесообразно определить как местоположение на второй ломаной в момент времени tk. За 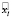 можно взять существующую точку на второй ломаной, ближайшую к моменту времени tk. Однако данный подход может существенно увеличить погрешность определения итоговой ошибки Eloss, так как ближайшая точка по времени может располагаться на значительном расстоянии от xk. Для нивелирования погрешности следует учитывать разницу во времени, что представляет собой нетривиальную задачу.
можно взять существующую точку на второй ломаной, ближайшую к моменту времени tk. Однако данный подход может существенно увеличить погрешность определения итоговой ошибки Eloss, так как ближайшая точка по времени может располагаться на значительном расстоянии от xk. Для нивелирования погрешности следует учитывать разницу во времени, что представляет собой нетривиальную задачу.
Второй способ определения 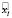 заключается в нахождении на второй ломаной двух точек
заключается в нахождении на второй ломаной двух точек 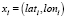 и
и 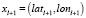 , предыдущей и следующей по отношению к моменту времени tk. Такой подход привнесет в определение ошибки Eloss не только оценку пространственной идентичности ломаных, но и временной. Следует учитывать, что в начале и/или в конце трека на одной из ломанных может не быть точек xl и/или xl+1. В этом случае ошибка пропорциональна расстоянию до существующей точки xl или xl+1:
, предыдущей и следующей по отношению к моменту времени tk. Такой подход привнесет в определение ошибки Eloss не только оценку пространственной идентичности ломаных, но и временной. Следует учитывать, что в начале и/или в конце трека на одной из ломанных может не быть точек xl и/или xl+1. В этом случае ошибка пропорциональна расстоянию до существующей точки xl или xl+1:
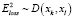 , (5)
, (5)
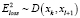 . (6)
. (6)
Если обе точки присутствуют на ломаной, имеем треугольник с геокоординатами xl, xl+1 и xk, и ошибка определяется как
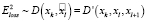 , (7)
, (7)
где D' – функция расстояния между точкой xk и дугой, составленной из точек xl и xl+1.
Рассмотрим подходы для определения функции D'.
1. Определение D' и 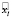 по скорости. В качестве
по скорости. В качестве 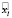 здесь рассматривается точка, которая находится на отрезке
здесь рассматривается точка, которая находится на отрезке 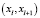 , на расстоянии dl,k от xl. При этом dl,k – расстояние, которое возможно преодолеть за время
, на расстоянии dl,k от xl. При этом dl,k – расстояние, которое возможно преодолеть за время 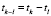 со скоростью spdl. Время tl здесь соответствует кортежу
со скоростью spdl. Время tl здесь соответствует кортежу 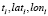 , spdl – моментальная скорость в точке xl. Итоговая ошибка определяется расстоянием между xk и
, spdl – моментальная скорость в точке xl. Итоговая ошибка определяется расстоянием между xk и 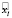 :
:
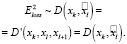 (8)
(8)
Однако скорость spdl может быть определена с большой погрешностью; движение в интервале времени от tl до tk может быть неравномерным, что предполагает учет ненулевого ускорения и/или градиентов ускорения, погрешность вычисления которых может лишь расти по отношению к погрешности определения spdl. В результате накопленная ошибка для 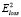 может быть значительна.
может быть значительна.
2. Определение D' как длины кратчайшего отрезка дуги от точки xk до отрезка дуги 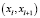 . При этом необходимо рассмотреть случаи, когда:
. При этом необходимо рассмотреть случаи, когда:
- точка 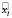 на дуге
на дуге 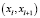 , которая лежит на кратчайшем отрезке дуги, не лежит на отрезке дуги
, которая лежит на кратчайшем отрезке дуги, не лежит на отрезке дуги 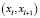 . В этом случае в качестве
. В этом случае в качестве 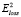 следует использовать расстояние до ближайшей точки:
следует использовать расстояние до ближайшей точки:
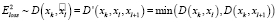 . (9)
. (9)
- точка 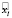 на дуге
на дуге 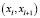 , которая лежит на кратчайшем отрезке дуги, лежит на отрезке дуги
, которая лежит на кратчайшем отрезке дуги, лежит на отрезке дуги 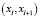 . В этом случае ошибка пропорциональна кратчайшему расстоянию:
. В этом случае ошибка пропорциональна кратчайшему расстоянию:
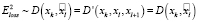 . (10)
. (10)
3. Определение D' как разницы расстояний. Данный подход предполагает расчет D' как разницы суммы расстояний от xl до xk, от xk до xl+1 и от xl до xl+1:
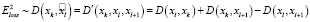 . (11)
. (11)
Иллюстрация приведена на рисунке.
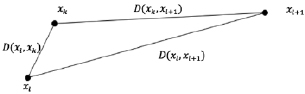
Иллюстрация расчета значения D' как разницы расстояний
Прямые между точками на рисунке эквивалентны дугам. Функция 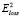 отражает оценку расстояния между xk и дугой
отражает оценку расстояния между xk и дугой 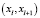 . Чем меньше
. Чем меньше 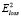 , тем ближе точка xk к дуге
, тем ближе точка xk к дуге 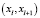 , чем больше – тем дальше. Если
, чем больше – тем дальше. Если 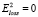 , точка xk лежит на дуге.
, точка xk лежит на дуге.
Исходя из минимизации погрешности и трудоемкости определения функции Eloss был выбран подход, учитывающий расстояние между точками в случае присутствия обеих точек в определенный момент времени на двух ломаных Lpredicted и LgroundTruth и разницу расстояний между точками (см. п. 3 выше) в противном случае.
Поскольку ошибка может быть неабсолютной величиной и не должна в общем случае отражать какие-либо параметры траектории движения, например сумму отклонений расстояний и др., знаки пропорциональности в формулах (1) и (9) заменим на знаки равенства. Общая ошибка Eloss будет являться квадратным корнем из среднеквадратической ошибки модели – отношения суммы квадратов расстояний 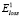 или
или 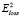 в зависимости от наличия или отсутствия обеих точек на двух ломаных соответственно к количеству точек:
в зависимости от наличия или отсутствия обеих точек на двух ломаных соответственно к количеству точек:
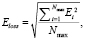 (12)
(12)
где 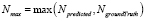 , так как вычисление ошибки должно быть выполнено для каждой точки ломаных Lpredicted и LgroundTruth;
, так как вычисление ошибки должно быть выполнено для каждой точки ломаных Lpredicted и LgroundTruth;
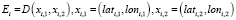 , при условии, что
, при условии, что 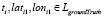 и
и 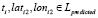 . В противном случае, когда на одной из ломаных нет точки в момент ti, т.е.
. В противном случае, когда на одной из ломаных нет точки в момент ti, т.е. 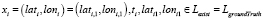 и
и 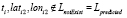 или
или 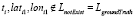 и
и 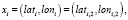
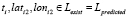 :
:
- 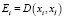 , при
, при 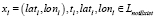 ,
, 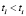 , если
, если 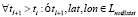 ;
;
- 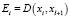 , при
, при 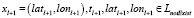 ,
, 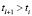 , если
, если 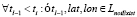 ;
;
- 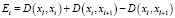 , при
, при 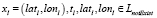 и
и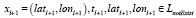 .
.
Стоит отметить, что алгоритм вычисления значения функции ошибки для одной траектории выполнится за линейное время, и его вычислительная сложность
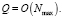 (11)
(11)
Заключение
В работе предложен метод расчета функции ошибки для оценки качества фильтрации геокоординат. Рассмотренный метод учитывает как оценку пространственной идентичности траекторий движения, так и временной, учитывая специфику предметной области задачи. Преимуществом метода является линейное время вычисления функции ошибки, что позволяет использовать его в качестве целевой функции при тренировке моделей машинного обучения в задачах фильтрации геокоординат, в том числе в переносимых мобильных устройствах. В качестве недостатка метода стоит отметить отсутствие учета метрики пространства в случае сравнения близости точки к отрезку дуги. Принимая во внимание скоростные и временные показатели движения, возможно сделать оценку более достоверной.



