В настоящее время прослеживается определенный исследовательский интерес к различным организационным структурам. В связи с этим активно развивается процесс моделирования, в том числе математического, как иерархических, так и гетерархических организационных структур. А именно для математического моделирования важнейшим моментом является процесс установления адекватности разработанной модели [1, 2]. То есть процесс установления адекватности однозначно отвечает на важнейший вопрос моделирования: соответствует ли разработанная математическая модель реальным (жизненным) процессам [3]. Кроме того, организационные структуры берут свое начало из природы, в частности гетерархия – это естественная и, соответственно, устойчивая организационная структура. Вследствие этого факта иерархия (особенно имеющая сложную структуру) должна рассматриваться с позиций искусственной организационной структуры, так как она является полной противоположностью гетерархии [4]. Изначально исследованием и описанием организационных структур занимались социологи, потому как в жизни эти системы присущи социальным группам, но постепенно происходит процесс переноса организационных структур на социально-экономические системы [5], и уже на данном этапе активно подключаются математики, которые, что естественно, по-своему осмысливают возникшую ситуацию, формулируют задачу и ставят вопросы, на которые хотят получить строгие ответы. Один из самых первых и, соответственно, наиважнейший вопрос, что будет являться неделимой и элементарной сущностью системы, в пределах которой действует любая организационная структура. В частности, для социальных групп такой сущностью, совершенно естественно будет являться человек, с позиций индивидуума. В принципе этот подход будет справедливым и для малых социально-экономических систем. Но если в качестве системы в рассмотрение вводится, например, региональный строительный кластер, а это уже достаточно большая социально-экономическая система, то уже в этом случае в качестве единичной сущности авторами предложено определять компании, относящиеся к этому кластеру. В качестве таких компаний (фирм) рассматриваются: инвесторы (девелоперы), застройщики, подрядчики, организации изыскателей и проектировщиков, фирмы – производители строительных материалов, и т.д. Именно эти организации и рассматриваются с позиций элементарных сущностей, составляющих региональный строительный кластер, причем необходимо отметить тот факт, что некоторые сущности могут входить в другие региональные кластеры, в частности это, например, относится к инвесторам.
В дальнейшем, для простоты изложения, будем называть сущности систем агентами, тем самым подводя читателей к идее выбора имитационного моделирования, которое является частью (важной) математического моделирования.
Постановка задачи
Введем в рассмотрение простейшую систему, где уже может возникнуть организационная структура, состоящую из двух агентов: агента_1 и агента_2. В течение жизни данной системы между агентами могут возникать связи и это в данном случае вероятностный процесс. Причем в первом случае агент_1 выступает инициатором возникшей связи, а во втором случае инициатором является агент_2. Естественно, связи возникают, некоторое время держатся и распадаются, причем они абсолютно несимметричны во времени даже у простейшей системы [6, 7]. Но уже в том случае появляется возможность смоделировать данные процессы с помощью систем массового обслуживания (СМО), причем в первом случае входящий поток будет ассоциироваться с агентом_1, а во втором случае – с агентом_2. Тут необходимо сделать небольшое отступление и обратиться к понятию системы массового обслуживания. Вообще говоря, это совершенно искусственная и абстрактная структура, которая функционирует по определенным правилам (дисциплинам прохождения заявок). Для любой СМО без очереди справедливым является тот факт, что входящая заявка либо мгновенно поступает на обслуживание (в случае одноканальной СМО), либо мгновенно получает отказ в обслуживании (если канал занят) и покидает систему (открытая СМО). Причем в нашем выборе простейшей системы речь может пойти, о СМО как с отказами, так и с очередями [8, 9]. Но именно использование СМО с очередями позволяет имитировать процесс установившихся связей между агентами. Кроме того, СМО случайность процесса как стохастичностью интервалов поступления, так и времени обслуживания в каналах. Таким образом, гетерархическую организационную структуру, а именно она была описана выше на простейшей системе, можно смоделировать посредством децентрализованного подхода к двум СМО с очередями.
В случае системы с тремя агентами (агент_1, агент_2 и агент_3) по сути появляется некая суперпозиция СМО, так как возникают цепочки связей где выходящий поток заявок из одной СМО неким образом добавляется к входящему потоку следующей СМО, а это уже говорит об использовании сетей массового обслуживания (СеМО) [10]. И кроме того уже появляются двухканальные СМО. Таким образом, можно сделать обобщенный вывод, что для моделирования гетерархической организационной структуры для системы из N агентов достаточно смоделировать многофазную СеМО где фазами будут являться СМО с очередями и с N – 1 каналами.
Теперь можно подходить к процессу установления адекватности разработанных СеМО. Любая СеМО состоит из фаз, имеющих последовательные или параллельные соединения, причем каждая фаза представляет собой СМО, в данном случае это система с ограниченным количеством мест в очередях. Таким образом, процесс установления адекватности разработанных СеМО сводится к установлению СМО, в нее входящих. Здесь необходимо сделать еще одно отступление и сделать анализ СМО с отказами. Эти системы также могут участвовать в качестве фаз при моделировании СеМО, описывающих гетерархическую организационную структуру в группе агентов, с некоторым допущением, а именно, любая заявка, получившая обслуживание в СМО, должна ставиться в соответствие с неким временным интервалом, например, если рассматривать его (интервал) как случайную величину, то зависящею от математического ожидания, и так же имеющую некий закон распределения. В этом случае моделируемая связь может быть в течении временного интервала устойчивой и размыкаться.
В рассмотрение вводятся два типа СМО с отказами: одноканальная и двухканальная. Для таких СМО, если удовлетворяют системам M/M/1 и M/M/2 (простейший входящий поток и экспоненциальный закон распределения обслуживающих устройств), то существует возможность аналитического расчета для функциональных характеристик, и именно данный факт будет являться основанием для установления адекватности разработанных СМО и СеМО. Все СМО разработаны в среде AnyLogic 8.2.3 с использованием библиотеки моделирования процессов (дискретно-событийный подход).
СМО с отказами и одним каналом обслуживания
На рис. 1 представлена блок-схема одноканальной СМО с отказами и основные свойства объектов, составляющих имитационную модель одноканальной СМО. Блок-схема включает в себя: объект Source (имитирует входящий поток), объект SelectOutput, объект Delay (имитирует канал обслуживания) и два объекта Sink и Sink1 (имитируют выходящий поток).
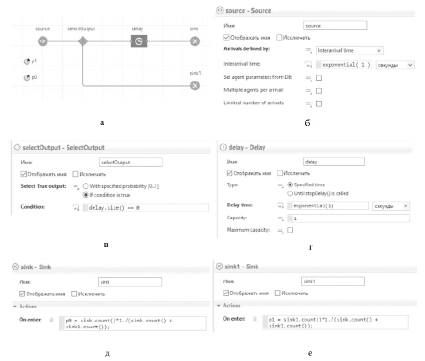
Рис. 1. a) блок-схема одноканальной СМО с отказами; б) основные свойства объекта Source; в) основные свойства объекта SelectOutput; г) основные свойства объекта Delay; д) основные свойства объекта Sink; е) основные свойства объекта Sink1
Здесь необходимо сделать некоторое отступление и рассмотреть процессы, возникающие в строительном кластере при гетерархической организационной структуре. Естественно, что работа всех компаний, входящих в данный кластер связана со строительством. Представим, что некий девелопер решил возвести жилой дом. Он связывается с компанией которая занимается изыскательскими работами, и данная фирма представляет для него канал обслуживания (Delay). По окончании изыскательских работ девелопер обращается к компании-проектировщику, тем самым открывая еще один канал (Delay), но с позиций СМО это будет одноканальная система, так как канал с застройщиком отработан и закрыт. При этом сам девелопер будет ассоциироваться с объектом Source – генератором заявок и т.д.
Кроме того, в модели определены две переменные p0 и p1. Они предназначены для хранения информации о вероятностях состояний системы. P0 – стационарная вероятность такого события, что поступившая в СМО заявка обнаруживает канал обслуживания свободным и мгновенно поступает на обслуживание. P1 – стационарная вероятность такого события, что поступившая в СМО заявка обнаруживает канал обслуживания занятым, мгновенно получает отказ и покидает систему.
Кроме того, для одноканальной СМО с отказами известны аналитические формулы [2], описывающие вероятности стационарного состояния системы. В частности, вероятность того что канал свободен,
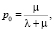
где l – частота плотности экспоненциального закона распределения простейшего входящего потока, m – частота плотности экспоненциального закона распределения интервалов обслуживания.
Вероятность того что канал занят,
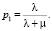
При запуске имитационной модели в обозначенной выше системе, существует возможность визуализации процесса прохождения заявок через объекты модели.
Видно (рис. 2), что в эксперименте было сгенерировано 49943 заявки, из них 24974 было обслужено в блоке Delay и поступило в бункер Sink, а остальные 24976 заявок поступили в систему с занятым каналом – получили отказ и поступили в объект-бункер Sink1. В имитационной модели l = m = 1 и, соответственно, p0 = p1 = 1/2, что абсолютно соответствует данным, рассчитанным в ходе имитационного эксперимента и хранящимися в переменных Р0 и Р1, которые равны 0,5.
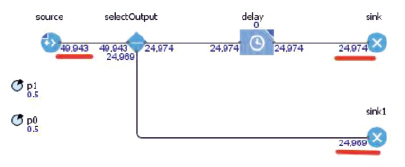
Рис. 2. Визуализация имитационного эксперимента одноканальной СМО
Рис. 3. a) блок-схема двухканальной СМО с отказами; б) основные свойства объекта Source; в) основные свойства объекта SelectOutput; г) основные свойства объекта Delay; д) основные свойства объекта Sink
СМО с отказами и двумя параллельными каналами обслуживания
На рис. 3 представлена блок-схема двухканальной СМО с отказами и основные свойства объектов, составляющих имитационную модель системы. Блок-схема включает в себя: объект Source (имитирует входящий поток), два объекта SelectOutput и SelectOutput1, два объекта Delay и Delay1 (имитируют каналы обслуживания) и три объекта Sink, Sink1 и Sink2 (имитируют выходящий поток). Кроме того, в модели определены шесть переменных P0, P1, Р2, P_otk, P_obs и P_obs1. Они предназначены для хранения информации о системе и в частности: P0 – стационарная вероятность такого события, что поступившая в СМО заявка обнаруживает каналы обслуживания свободными и мгновенно поступает на обслуживание любой канал (выбор канала осуществляется по равномерному закону распределения); P1 – стационарная вероятность такого события, что поступившая в СМО заявка обнаруживает один канал обслуживания занятым и мгновенно переходит на обслуживание в другой канал (естественно свободный) и P2 – стационарная вероятность такого события, что поступившая в СМО заявка обнаруживает оба канала обслуживания занятыми и мгновенно получает отказ и покидает систему. Переменная P_obs собирает информацию о количестве заявок, прошедших через канал, имитируемый объектом Delay. Переменная P_obs1 собирает информацию о количестве заявок, прошедших через канал имитируемый объектом Delay1. Переменная P_otk собирает информацию о количестве заявок, прошедших через False-порт объекта SelectOutput1. Необходимо обратить внимание на пользовательскую функцию FDistr(), присутствующую в блок-схеме. Данная функция используется для случайного выбора одного из каналов с использованием равномерного закона распределения (ситуация, когда все обслуживающие каналы свободны, а надо выбрать какой-то один). Ниже представлен программный код тела пользовательской функции FDistr() (язык программирования java).
Листинг функции FDistr()
if ((delay.size() == 0)&&(delay1.size() == 0)) {
int I_1 = uniform_discr(0,1);
Count++;
if (I_1 == 0){
c0 = true;}
else {
c0 = false;
c1 = true;}}
else {
c0 = delay.size() == 0;
c1 = delay1.size() == 0;}
Для объекта SelectOutput1 в поле условия используется переменная булевского типа с1.
Свойства объекта Delay1 совпадают с объектом Delay.
Свойства объектов Sink1 и Sink2 совпадают с объектом Sink.
Для двухканальной СМО с отказами известны аналитические формулы, описывающие вероятности стационарного состояния системы. В частности, стационарные вероятности равны
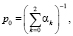
где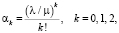 
l – частота плотности экспоненциального закона распределения простейшего входящего потока, m – частота плотности экспоненциального закона распределения интервалов обслуживания.
При запуске имитационной модели в обозначенной выше системе существует возможность визуализации процесса прохождения заявок через объекты модели (рис. 4).
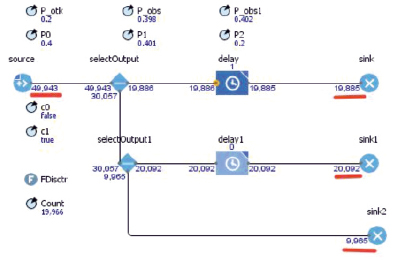
Рис. 4. Визуализация имитационного эксперимента двухканальной СМО
Видно, что в эксперименте было сгенерировано 49943 заявки, из них 19885 было обслужено в блоке Delay и поступило в бункер Sink, 20092 заявок было обслужено в блоке Delay1 и поступило в бункер Sink1 и 9965 заявок поступило в систему с занятыми каналами – получили отказ и поступили в объект-бункер Sink2. В имитационной модели l = m = 1 и, соответственно, p0 = 0,4, p1 = 0,4 и p2 = 0,2, что абсолютно соответствует данным, рассчитанным в ходе имитационного эксперимента и хранящимся в переменных P0, P1 и P2.
Кроме того, из результатов имитационного эксперимента видно, что нагрузка на каналы распределилась пропорционально частотам обслуживания в каналах, а так и должно быть, чему мы получили экспериментальное подтверждение.
Выводы
В данной работе было обоснованно применение СеМО для имитационного моделирования как гетерархической организационной структуры системы, так и иерархической. Показано, что даже при очень сложной топологии СеМО она (сеть) состоит из фаз, которыми являются СМО (причем как с очередями, так и с отказами). Разработаны и описаны имитационные модели СМО с отказами одноканальной и двухканальной систем. Проведены имитационные эксперименты и полученные результаты были сравнены с существующими аналитическими расчетами стационарных вероятностей физических состояний (система Колмогорова), установлено их соответствие. И на основании данного факта сделан вывод об адекватности как СМО, так и СеМО.