Применение математических методов при моделировании сложных процессов предполагает построение математической модели, формализованно представляющей проблемную ситуацию, где выявляется целевая функция, по сути, являющаяся формализацией цели моделирования. Очевидно, что возможно выделение нескольких вариантов решения или целевых альтернатив [1], которые являются логически непротиворечивыми и могут быть осуществлены, после чего осуществляется сравнение альтернатив, где наиболее объективной является оценка, получаемая путем вычислений и проведения экспериментов. Для задач принятия решений (задач оптимизации) в условиях определенности, компонентами такой модели являются множество всех (альтернативных) решений, из которых и делается выбор одного наилучшего или оптимального решения.
Постановка задачи
Наибольший интерес представляет моделирование технологических процессов [2, 3], когда математические модели охватывают весь процесс со сложными взаимосвязями между технологическими параметрами, что делает их основой для проведения расчетных экспериментов и позволяет проверить корректность решений и условий поставленных задач управления процессом. Методы получения математических моделей подразделяются на теоретические и экспериментальные. Теоретический метод заключается в аналитическом исследовании физической сущности процесса, а экспериментальный метод связан с обработкой данных, полученных непосредственно на физической модели процесса, с получением эмпирических выражений. Наиболее эффективным методом получения математической модели является сочетание теоретического и экспериментальных методов. Примерами использования теоретического метода являются моделирования процесса прецизионной корректировки дисбаланса цилиндрических инерционных тел и сферических узлов [4–6], что обеспечивается формированием на детали тонкопленочного покрытия с требуемым характером распределения массы покрытия по ее поверхности. В данном случае моделирование процесса, исходя из схемы корректировки дисбаланса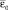 
, при которой в поперечном сечении цилиндра, или в диаметральном сечении сферического узла, центр окружности O* покрытия 2 смещен относительно геометрического центра О детали 1 на заданную величину δ в сторону, противоположную направлению вектора дисбаланса 
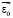(рис. 1), позволяет получить аналитическую зависимость смещения δ от величины дисбаланса 
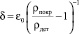, где ρпокр и ρдет – плотности материалов детали и покрытия [4, 6]. Для балансировки цилиндрической детали [4], задавая исходное условие в виде переменной скорости вращения цилиндра, математическое моделирование позволяет с известными допущениями получить целевую функцию, однозначно определяющую совокупность аргументов, выбор которых обеспечивает решение задачи. Конечные математические зависимости скорости напыления покрытия от угла поворота детали или времени процесса являются эмпирическими, поскольку учитывают экспериментальное определение используемых при моделировании констант.
Однако в ряде случаев возникают ситуации, когда в процессе моделирования появляются альтернативные варианты математических преобразований, позволяющие получить различные выражения для целевой функции. Это может быть связано с принятыми допущениями и предпочтениями при выборе аргументов. Поэтому важным аспектом моделирования сложного технологического процесса является корректная интерпретация возможных альтернативных целевых функций, полученных при формализации модели.
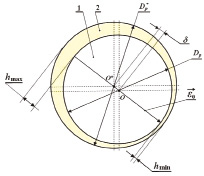
Рис. 1. Поперечное сечение детали с покрытием. 1 – деталь, 2 – покрытие, Dp и Dp* – диаметры до и после напыления, h – толщина покрытия, δ – разнотолщинность покрытия, ε0 – исходный дисбаланс
Цель работы заключалась в сравнительной оценке адекватности представленных в виде аналитических и эмпирических выражений целевых функций, полученных при моделировании технологического процесса корректировки дисбаланса сферических узлов.
Формирование целевых функций при моделировании процесса прецизионной балансировки сферических узлов
Определение аналитической зависимости. Моделирование процесса корректировки дисбаланса сферических узлов связано с решением задачи получения методом магнетронного напыления покрытия переменной толщины на поверхности узла [6] и основано на использовании обратной квадратичной зависимости скорости напыления vн от L – расстояния от сферического узла до источника напыляемого материала: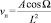 
[7], где 
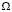– угол между направлением потока напыляемого материала и нормалью к поверхности ротора, А – размерная константа, определяемая параметрами процесса напыления. Исходное условие построения процесса напыления связано с управляемым изменением расстояния L от источника до вращающегося узла, т.е. с циклическим возвратно-поступательным перемещением узла. При этом амплитуда ΔL этого перемещения будет задавать характер изменения толщины покрытия, т.е. величину смещения δ, которая определяется как разность максимальной hmax и минимальной hmin толщины (рис. 1). Очевидно, что должна быть обеспечена согласованная взаимная ориентация вектора дисбаланса 
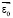и участков покрытия с толщинами hmax и hmin, определяемая с учетом требуемой величины конечного диаметра Dр* (рис. 1). Можно представить выражение для изменения угла Ω для произвольной точки на сфере при ее вращении: 
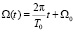, где t – данный момент времени, T0 – период вращения, Ω0 – начальное угловое положение рассматриваемой точки. А поскольку за один оборот сферы угол Ω меняется в пределах от Ω0 до 
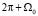, и угол Ω0 лежит в пределах от 0 до 2π, тогда диапазон изменения угла Ω составит 
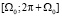в области от 0 до 4π, в которой и нужно определить функцию vн. Тогда
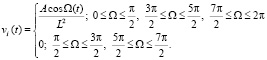. (1)
Закон возвратно-поступательного движения сферического узла, синхронизированного с его вращением, можно описать выражением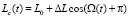 
, где Lc – текущее расстояние от источника до центра сферы, а L0 – среднее расстояние. А так как это выражение написано с учётом того, что в начальный момент времени сфера находится на минимальном расстоянии от источника, то можно написать:
,
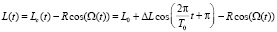где R – радиус сферы.
В итоге получается зависимость для толщины напыления за один оборот:
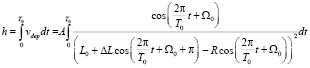, (2)
Выносим в знаменателе R за знак интеграла и, вычисляя дифференциал от выражения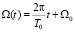 
, переходим к угловой переменной 
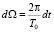и 
:
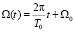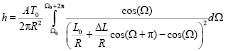. (3)
Обозначая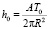 
, интеграл (4) можно преобразовать в выражение
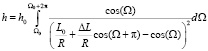, (4)
Здесь h0 является масштабной размерной константой, зависящей от радиуса сферы, периода вращения и параметров источника. Очевидно, что в интеграле (4) подынтегральное выражение равно нулю для угловых диапазонов, приведённых в выражении (1). С их учётом получаем конечное выражение для толщины покрытия за один оборот:
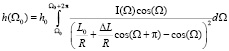, (5)
где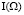 
– функция-индикатор:
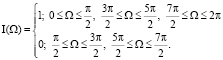. (6)
Поскольку интеграл (5) не выражается через простые функции, что ограничивает его практическую применимость, важно получить простое эмпирическое выражение, определяющее зависимость δ(L0, ΔL). Пренебрегая всеми угловыми множителями в выражении (5), запишем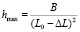 
и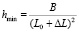 
, где B – некий численный коэффициент, зависящий от угловых множителей в выражении (5). Из очевидных геометрических соображений следует 
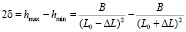, откуда после приведения к общему знаменателю получаем
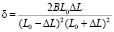. (7)
Для заданного значения δ можно определить величину ΔL, исключив константу В из конечной зависимости, т.е. представляя аналитическую зависимость амплитуды ΔL от требуемого смещения δ и задавая при этом значения расстояния L0 и средней толщины покрытия h. Согласно (рис. 1) смещение δ составляет величину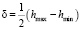 
, а средняя толщина покрытия 
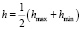, тогда их соотношение 
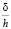после очевидных преобразований, разделив выражение 
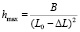на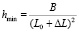 
и представив соотношение 
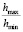в виде 
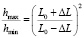, можно получить в виде зависимости
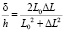, (8)
которая не содержит константы В и из которой определяется зависимость ΔL от δ и h.
Выражение (8) преобразуется в квадратное уравнение вида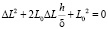 
, решение которого определяет требуемую зависимость
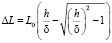. (9)
Очевидно, что второй корень квадратного уравнения (9) не имеет физического смысла, так как выражение в скобках больше единицы, что соответствует ΔL > L0, чего быть в принципе не может. Представленная зависимость позволяет установить требуемые значения амплитуды ΔL, поскольку использует выявленную на первом этапе величину смещения δ, определяемую дисбалансом ε0, и основана на задаваемом значении средней толщины покрытия h.
Определение эмпирической зависимости. Вместе с тем, предполагая, что допущения, основанные на исключении константы В, не позволяют получить требуемую точность расчета процесса балансировки, целесообразно экспериментально определить значение этой константы и использовать для расчетов эмпирические зависимости. Можно считать, что выражение (5) определяет толщину покрытия за 1 оборот для каждой точки поверхности сферического узла, и, следовательно, форму сферического узла после нанесения покрытия. Для получения численных результатов необходимо определить константу h0, используя эмпирические данные. Предположим, что без возвратно-поступательного движения за 30 минут на поверхности ротора осаждается слой вещества толщиной 1 мкм. Период вращения равен 3 сек, тогда за 30 минут сфера совершает 600 оборотов.
При значениях параметров: L0 = 80 мм, R = 5 мм, ΔL = 0 мм (поступательное движение отсутствует), получаем численное значение интеграла из выражения (5), равное 0,0086. Тогда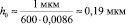 
. Таким образом, выражение (5) позволяет определить толщину напыления в любой точке поверхности сферы, включая значения hmax и hmin. Определив величину δ как разность 
, из выражения (5) можно построить зависимости смещения δ центра сферы от амплитуды ΔL возвратно-поступательного движения ротора при различных значениях L0, представленную на рис. 2. Чтобы определить константу B, аппроксимируем зависимости, полученные из выражения (5), выражением (7). Аппроксимация приведена на рис. 2, и с разумной точностью можно считать, что зависимость δ от ΔL и L0 определяется эмпирическим выражением (ΔL и L0 в мм):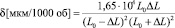 
, т.е. константа В = 0,825•104.
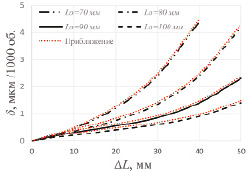
Рис. 2. Зависимости δ от ΔL для различных L0 , полученные численным расчетом и приближением (пунктир)
Интерпретация альтернативных целевых функций. Очевидный интерес представляет сопоставление результатов вычислений по зависимости (5), которые носят численный характер, и по аналитическому выражению (9), которое является приближенным, так как там используется допущение только обратной квадратичной зависимости величин hmax и hmin от максимального и минимального расстояния до источника, тогда как реальная функция предполагает зависимость от общего характера поступательно-вращательного движения, что и выражено интегралом по всему периоду в формуле (5).
Из рис. 3 видно, что разница в величинах ΔL для численного и аналитического вариантов расчета при конкретных значениях L0 и соотношений h/δ достигает ~ 25–30 % от данного ΔL. Поэтому использование выражения (9) возможно для приблизительной оценки условий формирования покрытия. Таким образом, приведенное аналитическое выражение хоть и не является точным математическим описанием объекта моделирования, но позволяет приближенно оценивать параметры процесса корректировки дисбаланса на уровне десятых долей микрометра без применения численных вычислений. Для более точных оценок (до тысячных долей микрометра) необходим расчет процесса по выражению (5). Основой для построения алгоритмов при реализации модели может являться эмпирическая зависимость (7), наименее общая, но наиболее удобная в применении.
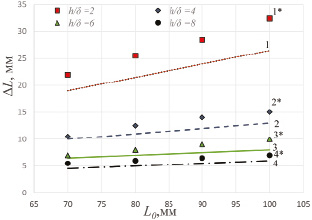
Рис. 3. Зависимость ΔL от L0 для заданных отношений h/δ. Линии 1, 2, 3, 4 – расчёт согласно формуле (9), линии из фигурных точек 1*,2*,3*,4* – результат, полученный по формуле (5)
Заключение
Определены условия моделирования процесса балансировки сферических узлов с интерпретацией альтернативных целевых функций и отработкой модели до достижения приемлемого уровня адекватности. Проверка адекватности модели доказала правомерность принятых при моделировании положений и требуемую точность моделирования, с получением как качественного, так и количественного согласия результатов. Обоснованы преимущества использования математических моделей, в том числе и посредством экспериментальной проверки, выраженных в виде эмпирических зависимостей, в которых используются константы, определяемые условиями процесса формирования покрытия и учитывающие интегральную зависимость изменения толщины покрытия от угла поворота сферического узла относительно потока напыляемого материала.