При исследовании позвоночника с целью диагностики грыж межпозвонковых дисков, внутримозговых опухолей спинного мозга и других процессов используют как компьютерную, так и магнитно-резонансную томографию. При этом МРТ является более предпочтительным методом исследования, так как позволяет визуализировать мягкие ткани с высокой контрастностью. Наиболее часто, для диагностики получают Т1-, Т2-взвешанные изображения.
При работе с МРТ изображениями заключение врача-рентгенолога строится на визуальном сравнении окружающих тканей на снимке, а применяемые методы оценки основываются на различиях в контрасте, размерах и пространственном положении патологий на изображении. Такой подход может привести к неверной интерпретации данных и, как следствие, к неправильному диагнозу, из-за схожести визуальной МРТ картины для разных патологий или различий визуальной картины органов в норме, полученной с разных томографов. Данные, подтверждающие возможные ошибки в интерпретации визуальной МРТ картины, были приведены во многих работах [1–2].
Одной из составляющих, ограничивающей методы оценки для диагностики по классической МРТ (позволяющей получать Т1-, Т2-взвешанные изображения), является то, что интенсивность пикселя на изображении зависит не только от биофизических свойств ткани, но и от примененных протоколов и времен захвата (TE, TR) при настройке томографа [3]. Протоколы и времена захвата различаются у разных производителей томографа, а также могут быть изменены лаборантом по усмотрению врача-радиолога. В связи с этим интенсивность пикселей на полученном изображении, отраженная в оттенках серого (grey value), может сильно различаться для одного пациента, обследованного на разных томографах.
В связи с численным различием интенсивности пикселей на снимках МРТ, полученных с разных томографов, для врача-радиолога МРТ изображение предоставляет только качественную информацию. Значения интенсивности не позволяют численно оценивать области интереса на снимке и сравнивать численные значения интенсивности между разными пациентами, или со значениями для ткани в норме и при патологии.
Для повышения точности постановки диагноза по МРТ изображениям врачу-радиологу, к качественной информации о различии контраста (в терминах гипер-, гипо-интенсивный) и пространственному положению, необходимо ввести количественный признак [4]. Такой признак должен оцениваться как характеристика ткани в норме и при патологии. Задача получения количественного признака на основе интенсивности пикселей МРТ изображения не является тривиальной и требует решения нескольких локальных задач.
Для применения в диагностике количественные признаки должны быть воспроизводимы, то есть измеренные параметры должны определяться взаимной близостью, при исследованиях, выполненных с различными условиями, такими как разные фирмы томографов и различные времена захвата, и импульсные последовательности. Как было сказано ранее, значения интенсивности, полученные при классических МРТ (Т1-, Т2-взвешанные изображения), различаются между собой в изображениях в зависимости от использования разных настроек томографа. Отсюда следует, что интенсивность пиксела от Т1-, Т2-взвешенных изображений не могут быть использованы в качестве количественного признака в диагностике в чистом виде. Так как воспроизводимость является важным требованием к количественным признакам, то для использования значений интенсивности в качестве оценочного признака необходимо осуществить обработку, направленную на восстановление интенсивности относительно параметров томографа. Проблема, связанная с восстановлением интенсивности на МРТ изображениях, осложняется не только многообразием томографов и их настроек, но и изменениями интенсивности, вызванными неоднородностью магнитного поля и нелинейностью градиента.
Другой характеристикой количественного признака является его способность идентифицировать патологический процесс, путем сравнения численных значений с принятыми нормами для здоровой или поражённой ткани. В ходе литературного обзора были найдены шкалы классификации патологического процесса, при диагностике по МРТ изображениям. Они основаны на разности контраста (в терминах гипер-, гипоинтенсивный) в сочетании с формой и размером образования. Данные шкалы являются визуальными и ни одна из них не использует численные значения интенсивности МРТ изображения. Таким образом, из-за того, что значения интенсивности численно не соотносятся с стандартизированной оценочной шкалой, необходимо рассмотреть методы сопоставления восстановленной интенсивности МРТ с значениями, нормированными по оценочной шкале. В данной работе предлагается сопоставлять восстановленную интенсивность МРТ с радиологическими свойствами ткани, такими как коэффициент ослабления рентгеновского излучения с последующей их привязкой к оценочной шкале Хаунсфилда.
В качестве примера, в компьютерной томографии на этапе диагностики врач-радиолог, помимо качественной информации о визуальной картине патологической области на снимке и ее пространственном расположении, имеет возможность получить дополнительный признак, выполнив количественные измерения, заключающиеся в определении плотности в единицах шкалы Хаунсфилда [5]. Каждой здоровой ткани (органу) в теле человека или патологии ставится в соответствие определенный диапазон плотностей в единицах шкалы Хаунсфилда, тем самым у врача-радиолога появляется дополнительная опора при постановке диагноза.
В соответствии с поставленными критериями к количественному признаку, для использования значений интенсивности от МРТ изображений в качестве дополнительного диагностического признака, необходимо решить две группы задач:
– уменьшить влияние томографа и его настроек на изменчивость интенсивности, а также устранить артефакты неоднородности магнитного поля и нелинейности градиента, которые вносят изменения в интенсивность;
– получить модель перевода МРТ данных в другую модальность, путем сопоставления восстановленной интенсивности МРТ с рентгенологической плотностью (от КТ), используя методы математической статистики.
Модель перевода модальности. При МРТ и КТ исследовании сканируется один и тот же объект, однако сигналы, зарегистрированные с МРТ, не соответствуют значениям, полученным в результате КТ. Интенсивности МРТ коррелируют с плотностью протонов и временами магнитной релаксации, но не коэффициентом ослабления рентгеновских лучей. Отсутствие соответствия между интенсивностью МРТ и рентгенологическими свойствами ткани приводит к необходимости рассмотрения подходов математической статистики по сопоставлению результатов исследования КТ и МРТ.
В ходе литературно-аналитического обзора были проанализированы подходы к сопоставлению данных от медицинских изображений разной модальности. Целью таких подходов является как определение общих свойств или различий между исследуемой областью интереса, так и установление зависимости между ними по выбранному признаку.
Рассмотренные подходы к сопоставлению и установлению зависимости можно разделить на следующие:
1 подходы, основанные на сегментации областей интереса со статическим распределением значений;
2 подходы, основанные на использовании атласов;
3 подходы, основанные на методах обучения нейронных сетей;
4 подходы, основанные на функции отображения.
Подход на основе сегментации
Данный подход заключается в сегментировании изображения по разным типам тканей и назначении сегментированным областям заранее определенных значений. В частности, по результатам сегментации МРТ изображения каждой сегментированной области может быть назначено значение в единицах Хаунсфилда. Подход на основе сегментации рассмотрен в работах [6–7]. Такой подход ограничивается областью применения из-за сложности анатомической структуры в теле человека. Также такой подход действителен лишь для небольшого значения типов тканей с ранее известными значениями плотности Хаунсфилда и не обеспечивает определение значений для несегментированных структур.
Подход на основе использования атласов
Данный подход заключается в наличии базы данных с набором изображений, полученных при разном виде неинвазивного исследования. В ходе такого подхода выполняется поиск наиболее схожего атласа в базе данных, по морфологическим признакам [8–9]. В отличие от методов сегментации рассмотренных ранее, подход основанный на атласах, позволяет назначить не заранее установленный диапазон значений плотности для выбранной области, а множество значений из схожего клинического случая, входящего в набор атласа. Недостатком такого подхода является необходимость использования большой базы данных изображений от разных исследований и решения задач арбитража между несколькими схожими снимками из атласа.
Подход на основе методов обучения нейронных сетей
Использование методов машинного обучения в рамках рассматриваемых подходов заключается в выявлении закономерностей между наборами данных, путем обучения на прецедентах, на основе ранее рассмотренных медицинских изображений. Такой подход может использоваться для определения вероятности нового значения для каждого пикселя. Подходы на основе машинного обучения различаются в соответствии с используемыми алгоритмами обучения [10–11]. Достоверность подходов на основе машинного обучения определяется наличием большого количества учебных данных, а также правильного подбора учебных данных и эффективности обучения.
Подход на основе функции отображения
Подход на основе функции отображения заключается в расчете и применении функции для преобразования значений интенсивности. Данный подход состоит в попиксельном присвоении интенсивности МРТ новых значений, таких как электронная плотность. В таком подходе применяются методы математической статистики для описания зависимости данных на небольшой выборке и использование полученной зависимости к данным, не вошедшим в выборку. В работе Rank CM et al. [12] был рассмотрен метод анализа дискретной функции, заключающийся в прогнозировании одной категориально-зависимой переменной к одной или нескольким независимым переменным. Метод регрессии на основе смесей распределения был рассмотрен в работах [13]. В данной работе в качестве функции распределения была выбрана гауссова функция. Точность полученных результатов напрямую зависит от количества выбранных смесей и правильности поиска экстремума в целевой функции. Такие методы не берут во внимание пространственное положение, а действуют пиксель за пикселем.
Для решения задачи по переводу данных в новую модальность, к подходам, по сопоставлению восстановленной интенсивности МРТ с плотностью в единицах Хаунсфилда, предъявляются следующие критерии:
1. Область применения (ОП) – критерий определяет применимость подхода для одной отдельной выделенной области интереса или нескольких.
2. Объём обучающей выборки (ООВ) – критерий, определяющий количество необходимых исходных данных для произведения настройки (оптимизации параметров) модели зависимости.
3. Ресурсоемкость (Р) – критерий, определяющий количество данных, хранимых в памяти компьютера и используемых для получения результата.
4. Сложность реализации (СР) – критерий, определяющий сложность алгоритмического описания рассматриваемого подхода.
5. Точность подхода (ТП) – критерий, определяющий возможность определить достоверность полученных результатов.
В ходе оценки рассмотренных подходов по сопоставлению данных МРТ данным КТ, при парных сравнениях использовалась шкала словесных определений уровня важности.
Общая картежная модель оценки аналогов (ОА) методов к сопоставлению данных от медицинских изображений разной модальности:
ОАп = <О(ОП), О(ООВ), О(Р), О(СР), О(ТП); R>, (1)
где О – оценка; R – матрица связей.
Область применения. Данный критерий будем оценивать по двухбалльной шкале:
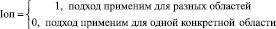
Объём обучающей выборки. Данный критерий будем оценивать по трехбалльной шкале:
Ресурсоемкость. Данный критерий будем оценивать по двухбалльной шкале:
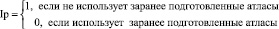
Сложность реализации. Данный критерий будем оценивать по трехбалльной шкале:
Точность подхода. Данный критерий будем оценивать по двухбалльной шкале:
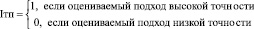
Таким образом формула для оценки аналогов принимает вид
+ 
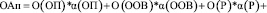
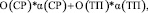(2)
где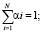 
αi – весовой коэффициент i-го критерия.
Оценка производилась с использованием методики Томаса Саати. Итоговая оценка рассмотренных групп подходов по критериям представлена в таблице.
Оценка подходов сопоставления данных МРТ и КТ по критериям
|
ОП |
ООВ |
Р |
СР |
ТП |
α |
|
|
Интегральная оценка |
0,22 |
0,21 |
0,10 |
0,05 |
0,42 |
1 |
|
подходы, основанные на сегментации областей интереса с статическим распределением значений; |
0 |
0,21 |
0,10 |
0,05 |
0 |
0,36 |
|
подходы, основанные на использовании атласов; |
0 |
0,21 |
0,10 |
0 |
0,42 |
0,73 |
|
подходы, основанные на методах обучения нейронных сетей; |
0,22 |
0 |
0 |
0 |
0,42 |
0,64 |
|
подходы, основанные на функции отображения |
0,22 |
0,105 |
0,10 |
0,025 |
0,42 |
0,87 |
Проведенная оценка подходов позволяет сделать следующий вывод. Наиболее удовлетворяющим заданным критериям является подход, основанный на функции отображения полученной как результат использования алгоритмов регрессии математической статистики. Такой подход позволяет получить математическую модель, описывающую зависимость между данными разной модальности, используя небольшой набор пар входных данных для исследования. Однако точность сопоставления данных МРТ и КТ при использовании данного подхода будет зависеть от правильности подготовки исходных данных для расчета коэффициентов регрессии. Таким образом, на подготовительном этапе статистических расчетов необходимо дополнить данный подход алгоритмами устранения перепадов интенсивности, вызванных неоднородностью магнитного поля и алгоритмами усреднения интенсивности относительно параметров томографа, и использовать данные алгоритмы на этапе оценки. Также подход, основанный на обработке попиксельно, использует информацию лишь об интенсивности пикселей и не использует информацию о пространственном расположении пикселя, то есть не учитывает, от какой анатомической структуры были получены значения интенсивности.
Таким образом, проблема в области медицинской визуализации на этапе диагностики, связанная с отсутствием стандартизированной оценочной шкалы для значений интенсивности на МРТ, и их численным различием между изображениями, полученными с разных томографов, и настройками, является предпосылкой к выдвижению гипотезы: разработать модель оценки МРТ изображений на основе значений интенсивности, нормированных по шкале Хаунсфилда, используя функцию отношения между значениями МРТ и КТ. Данная модель должна быть способна нормализовать значения интенсивности от разных МРТ изображений и соотнести их с соответствующими им плотностными значениями в единицах Хаунсфилда с учетом их пространственного положения. Предполагается, что создание такой модели позволит повысить качество диагностики путем получения информации о рентгенологической плотности по результатам МРТ без использования КТ. Кроме того, использование такого метода уменьшит количество сканирований КТ и связанный с ними дискомфорт для пациентов и уменьшит связанные со сканированием затраты.
Для описания специфики предлагаемого решения нами был разработан пакет структурных и математических моделей.
Общая схема предлагаемого решения по извлечению из МРТ изображения количественных признаков и оценки их в соответствии со шкалой Хаунсфилда приведена на рис. 1.
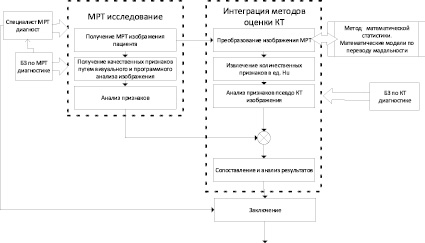
Рис. 1. Общая схема предлагаемого решения
Для наиболее полного понимания процесса функционирования разрабатываемого метода оценки была создана функционально-структурная модель в соответствии с Р50.1.028-2001. Для построения моделей использовано программное средство AllFusion Process Modeler 7.3.
На рис. 2 приведена функционально-структурная модель проектируемого решения нулевого уровня, отображающая входящие и исходящие данные на этапе работы с МРТ изображением, а также механизмы управления и функционирования в целом.
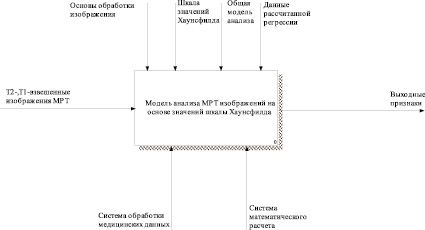
Рис. 2. IDEF0-модель TO-BE нулевого уровня
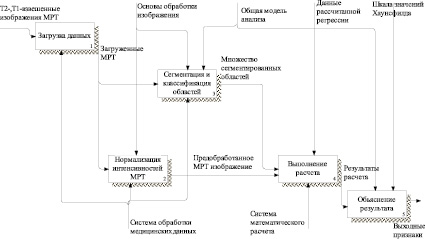
Рис. 3. IDEF0-модель TO-BE первого уровня
На рис. 3 приведена функционально-структурная модель проектируемого решения первого уровня. На ней отображены основные направления деятельности системы, представляющие собой подсистемы данной системы.
Описываемая модель состоит из следующих подсистем:
1. Подсистема загрузки данных.
2. Подсистема нормирования интенсивностей.
3. Подсистема сегментации.
4. Подсистема объяснений.
5. Подсистема расчета.
Подсистема загрузки данных
Подсистема должна принимать на вход МРТ изображения одного пациента, для расчета плотностных значений шкалы Хаунсфилда, используя ранее рассчитанную модель. Загружаемые файлы должны находиться в формате DICOM, при необходимости подсистема должна преобразовывать входную информацию для дальнейшей работы других подсистем.
Подсистема нормирования интенсивностей
На вход подсистемы подается матрица интенсивностей изображения и данные о параметрах сканирования из тегов DICOM. Выполняются алгоритмы по устранению искажения интенсивности, полученные при МРТ исследованиях с применением различных импульсных последовательностей и с различными настройками времен захвата. Устраняются перепады интенсивности, вызванные неоднородностью магнитного поля, и усредняются интенсивности относительно параметров томографа.
Подсистема сегментации
Подсистема классифицирует анатомические структуры на изображении, получая сетки для каждого класса. Для каждой сетки используется свой набор смесей распределения для выполнения расчетов в следующей подсистеме.
Подсистема расчета
На вход, в систему расчета, поступает множество значений интенсивности и множество сеток (сегментированных областей). При расчете значений шкалы Хаунсфилда от значений интенсивности МРТ одной сегментированной области выполняется итеративное сложение значений от весов вероятности и элементов ковариационной матрицы в соответствии с примененным математическим аппаратом. Все веса вероятности и матрицы были рассчитаны по тестовой выборке с применением порождающей модели смеси распределения [14]. При расчете параметров модели по набору пар значений выполняется EM-алгоритм. Условием для прекращения итераций алгоритма является заданный порог для логарифмической вероятности. На выход из подсистемы поступают данные необходимые для анализа, в виде значений шкалы Хаунсфилда.
Также нами был предложен пакет математических моделей. Основная идея, изложенная в модели, заключается в возможности определения рентгенологической плотности в единицах шкалы Хаунсфилда только лишь по результатам МРТ.
Дано: набор пар изображений МРТ и КТ одного пациента.
Требуется: синтезировать математическую модель метода определения рентгенологической плотности в значениях шкалы Хаунсфилда по МРТ изображению.
Порядок проведения эксперимента. Были получены серии изображений КТ и МРТ одного и того же пациента. Каждое изображение представлено множеством значений интенсивности. Область на снимках – шея. Из-за того, что связь между значениями коэффициента ослабления в КТ и интенсивностью в МРТ не может быть получена по уравнениям, описывающим рентгеновские явления и явления ЯМР, для получения регрессионной функции предлагается использовать статистические методы регрессии, опираясь на совместное сопоставление значений КТ и МРТ от одной и той же области интереса. К изображениям применяются алгоритмы устранения артефактов, вызванных неоднородностью магнитного поля, нелинейности градиента, артефакты химического сдвига. На изображении выделяются основные анатомические структуры, такие как спинномозговая жидкость, спинной мозг, пульпозное ядро, жир, мышцы шеи, воздух. Для каждой из сегментированных анатомических структур выполняется фиксация значений интенсивности Ii, где i – номер области захвата на изображении, и вычислено среднее значение в каждой из структур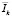 
, где k – номер класса анатомической структуры. Для выбранного в аналогах протокола исследования влияние времен релаксации Т1 сводится к минимуму, из-за большого TR, что позволяет оценить сигнал уравнением
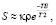(3)
где κ – константа, зависящая от используемого томографа,
ТЕ – время эхо, величина характеризующая настройки выбранного протокола.
Из уравнения видно, что контраст между тканями определяется величиной Т2 и ρ. Самую наибольшую протонную плотность и наименьшую разницу значения времен релаксации Т2, полученных в разных экспериментах согласно данным, приведенным в статье J.Z. Bojorquez [15], имеют жировые структуры, что делает его наименее чувствительным к различиям МР-исследования.
Поскольку значения интенсивности в МРТ изображениях варьируются, при разных настройках протокола (переменная TE для выбранных настроек протокола), необходимо для каждого значения интенсивности МРТ рассчитать интенсивность Ii* в долях относительно средней интенсивности, полученной от жира в этом изображении:
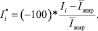(4)
Полученные значения Ii* для разных тканей сравнимы между Т2-взвешенными МРТ изображениями, полученными при разных временах захвата и силы магнитного поля.
Сопоставив совместно значения плотности в единицах шкалы Хаунсфилда по КТ изображениям и значения интенсивности* МРТ изображения в каждой из областей было получено множество пар значений (x, y), где x – значение Ii* МРТ изображения, а y – соответствующее ему значение КТ, для дальнейшего расчета регрессии в соответствии с выбранным аналогом.
Для описания сложных форм распределений полученных пар значений воспользуемся уравнением порождающей модели смеси распределения [14]:
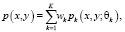(5)
где pk(x, y; θk) – функция правдоподобия k-й компоненты;
wk – веса k-й компоненты модели;
θk – вектор параметров распределения.
Параметр θk = (μk, Σk), где μk – математическое ожидание, Σk – ковариационная матрица. Использование смеси распределения позволит описать сложные формы распределения пар значений. В качестве функции плотности распределения в модели смеси используется гауссова функция распределения (6), а модель смеси называется гауссовой смесью.
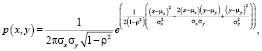(6)
где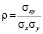 
– коэффициент корреляции.
При разделении смеси происходит подбор параметров θ и w, таким образом, чтобы доставить максимум функции правдоподобия. Для оценки параметров используем алгоритм EM, состоящих из двух этапов:
1) оценка параметров:
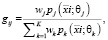(7)
где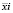 
– i-й вектор значений (x, y) в выборке;
i = 1,..,m – номер вектора в выборке;
j = 1,..,K – номер компоненты смеси.
2) подбор параметров:
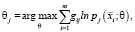(8)
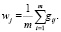(9)
После оценки параметров для заданных пар значений уравнение (5) можно использовать для регрессии. Для этого представим двумерную функцию распределения плотности как произведение условной плотности y и плотности x и выразим условную плотность y:
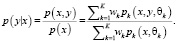(10)
Запишем уравнение (10) в следующем виде:
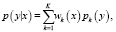(11)
где
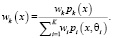(12)
Предполагаемое значение в единицах шкалы Хаунсфилда по заданному значению интенсивности МРТ можно получить как условную среднюю:
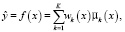(13)
где
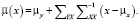(14)
Используя рассчитанные значения матрицы ковариации и веса вероятности, для исходного набора данных, становится возможным рассчитать плотностные значения в единицах шкалы Хаунсфилда для нового МРТ изображения, не входящего в исходную выборку, используя уравнение (13), где x – нормализованные значения интенсивности МРТ.
Выводы
Таким образом, научная новизна заключается в том, что предлагаемое решение позволяет получить дополнительный количественный диагностический признак из МРТ изображений, нормированный по оценочной шкале Хаунсфилда.
В ходе работы были получены как научные, так и практические результаты:
1. Рассмотрены особенности задачи оценки классических МРТ изображений (Т1-, Т2-взвешенных изображений), направленных на диагностику патологий позвоночника. Проанализированы требования к количественным диагностическим признакам. Показана перспективность и актуальность предлагаемой разработки.
2. Проведен литературно-аналитический обзор существующих методов восстановления интенсивности с учетом настроек томографов и артефактов неоднородности и нелинейности и подходов по сопоставлению данных разной модальности. Была выдвинута гипотеза предлагаемого решения.
3. Предложена концепция модели оценки МРТ изображений на основе значений, нормированных по шкале Хаунсфилда.