Для очистки прибордюрных зон улиц от смерзшихся отложений грунто-ледовых масс предлагают применять режущие рабочие органы [1, 2], в том числе торцевую фрезу [3]. Фреза представляет собой вращающийся диск с закрепленными на нем резцами на упругих подвесах [4]. Стабильное положение резцов при работе фрезы в плоскости резания определяет характер взаимодействия сил сопротивления в точке приложения основного усилия резания к резцу фрезы.
Если крепление резца происходит на одном подвесе, который выполнен из отрезка троса (стального каната), при контакте резца с смерзшейся массой его положение дестабилизируется и резец отклоняется и выходит из плоскости резания. В результате угол резания и направление усилия резания меняются (рис. 1, а). Если резец крепится на двух продольно расположенных подвесах, то за счет изгиба упругих стержней по схеме, показанной на рис. 1, б, появляется возможность удержания резца в режущей плоскости при отклонении резца с подвесом.
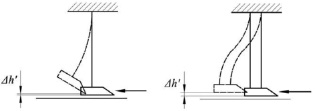
а) б)
Рис. 1. Схемы отклонения подвеса при случайном контакте резца под действием суммарного с дорожным покрытием отклоняющего усилия
Расчетная система определения сил взаимодействия при закреплении резца на двух параллельных подвесах, смещенных в продольном направлении, становится статически неопределимой системой [5]. Контур данной системы образуют элементы: «Диск – подвес передний – резец – подвес задний – диск». Это переводит задачу расчета образовавшейся рамы к трижды неопределимой системе.
В связи с отсутствием в литературе сведений по возможности и стабилизации резцов путем закрепления их на двух подвесах и по механизму отклонения резца в точке сопротивления среды возникает необходимость проведения аналитического и экспериментального исследований силового взаимодейстия резца при контакте с твердым полотном дороги.
Цель исследования
Выполнение анализа смещения резца при совместном действии силы резания и реакции дорожного полотна. Оценка возможности стабилизации положения резца при его закреплении на двух параллельных упругих подвесах.
Результаты исследования и их обсуждение
В процессе резания на резец действует внешняя нагрузка случайного контакта его с дорогой, которую можно разложить на две составляющие: силу резания Fτ, направленную параллельно плоскости дорожного полотна, и его вертикальную реакцию Fz, направленную перпендикулярно плоскости дороги. Рассмотрим рис. 2, а, на котором представлена исходная система усилий.
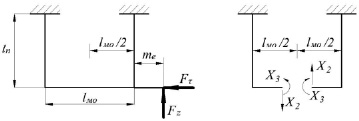
а) исходная система усилий б) основная система усилий
Рис. 2. Схемы исходной и основной систем
Параметр me является вылетом режущей кромки лезвия относительно оси переднего подвеса.
Для расчета данной статически неопределимой системы нами выбрана основная система, освобожденная от дополнительных связей и представленная на схеме рис. 2, б.
В результате замены отброшенных связей силовыми факторами Х1, Х2, Х3 система становится статически определимой. Данные силовые факторы имеют следующие смыслы: Х1 – неизвестное продольное усилие в резце; Х2 – неизвестное поперечное усилие в резце; Х3 – неизвестный изгибающий момент в резце.
Полученная статически определимая система имеет 6 неизвестных, а степень статической неопределимости ее остается равной трем. Это позволяет составить три канонических уравнения системы, после решения которых путем раскрытия статической неопределимости методом сил [6] будут определены 3 неизвестных фактора.
В этом случае для трижды статически неопределимой системы система канонических уравнений метода сил примет вид
δ11?X1 + δ12?X2 + δ13?X3 + Δ1P = 0, (1)
δ21?X1 + δ22?X2 + δ23?X3 + Δ2P = 0, (2)
δ31?X1 + δ32?X2 + δ33?X3 + Δ3P = 0, (3)
где δik – единичные коэффициенты канонических уравнений;
ΔiP – грузовые коэффициенты канонических уравнений.
1-е уравнение приводит к нулю взаимное сближение или удаление среднего сечения резца (в плоскости симметрии системы).
2-е уравнение приводит к нулю взаимный сдвиг среднего сечения резца (в плоскости симметрии системы).
3-е уравнение приводит к нулю взаимный поворот среднего сечения резца (в плоскости симметрии системы).
Коэффициенты уравнений определяются способом Верещагина путем перемножения единичных и грузовых эпюр [7].
После определения единичных и грузовых коэффициентов нами получены следующие решения канонических уравнений:
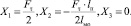
Это позволило получить следующие эпюры внутренних силовых факторов (рис. 3).
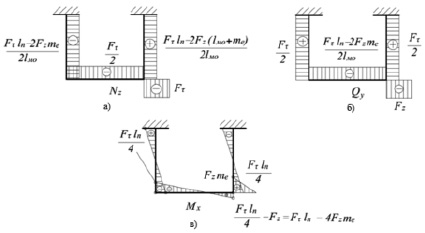
Рис. 3. Итоговые эпюры: продольных усилий (а), поперечных усилий (б) и изгибающих моментов (в)
Уравнение изогнутой оси каната можно представить в виде момента Mx(z):
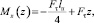 (4)
(4)
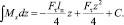 (5)
(5)
При сохранении резца в плоскости резания угол поворота каната в заделке равен нулю, и постоянная величина интегрирования «С» также равна нулю (С = 0).
После вторичного интегрирования получаем
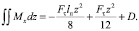 (6)
(6)
Постоянная интегрирования «D» может быть определена из условия равенства нулю смещения каната в заделке (D = 0).
Само смещение (Δ) как функция продольной координаты z определится выражением
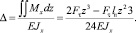 (7)
(7)
Следовательно, при z = lп смещение резца равно
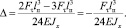 (8)
(8)
При условии использования в качестве материала подвесов троса (стального каната) диаметром 19 мм ГОСТ 3063-80 [8] величина смещения резца с рациональными геометрическими параметрами подвеса, закрепленного на двух продольных подвесах, Δ2 снижается в 8 раз по сравнению с одноподвесной системой Δ1:
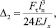 (9)
(9)
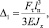 (10)
(10)
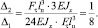 (11)
(11)
Выполнен расчет смещений резца при образовании изгибных усилий в подвесах от реакции дорожного покрытия (рис. 2, а) в точке контакта с резцом.
Ввиду сохранения основной системы все единичные коэффициенты канонических уравнений не претерпят изменений, поэтому достаточно выполнить определение только трех грузовых коэффициентов, которые имеют значения
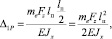 (12)
(12)
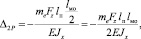 (13)
(13)
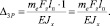 (14)
(14)
В итоге это дает следующие решения канонических уравнений:
X1 = 0, (15)
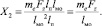 (16)
(16)
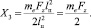 (17)
(17)
В соответствии с уравнениями получены итоговые эпюры внутренних силовых факторов, показанных на рис. 3.
Анализируя полученные эпюры, можно заметить, что нормальная реакция дорожного полотна приводит к сжатию переднего подвеса усилием 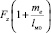 и растяжению заднего усилием
и растяжению заднего усилием 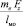 . При этом их значения по сравнению с усилиями деформации изгиба ничтожно малы. Реакция дорожного полотна не вызывает изгиб подвесов, а приводит к плоскопараллельному смещению резца.
. При этом их значения по сравнению с усилиями деформации изгиба ничтожно малы. Реакция дорожного полотна не вызывает изгиб подвесов, а приводит к плоскопараллельному смещению резца.
Принцип независимости действия сил гласит, что совместное действие силы резания и нормальной реакции дорожного полотна определится алгебраической суммой каждой из внешних сил. Представим исходную систему, на которую воздействуют обе силы (Fτ, Fz), схемой представленной на рис. 4.
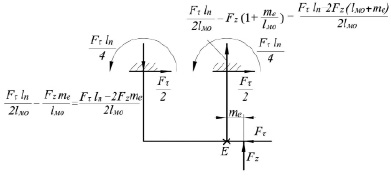
Рис. 4. Исходная система сил
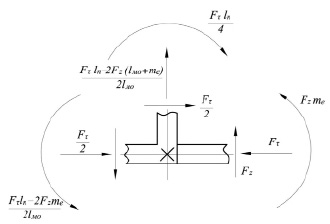
Рис. 5. Схема проверки адекватности раскрытия системы
Правильность раскрытия статической неопределимости подтверждает равновесие узла (×Е), в котором сходятся 3 силовых участка (передний подвес – режущая кромка резца – корпус резца) (рис. 5).
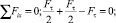 (18)
(18)
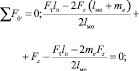 (19)
(19)
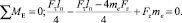 (20)
(20)
Поскольку в узле Е устанавливается равновесие сил, то адекватность раскрытия статической неопределимости системы крепления резца на двух подвесах правомерна. Кроме того, очевидно, что равноопасное сечение обоих подвесов в системе находится в верхней и нижней заделках.
В каждой их них изгибающий момент равен 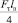 .
.
Режущая способность резцов фрезы ограничена пределом текучести материала проволок каната σт. Тогда
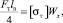 (21)
(21)
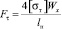 . (22)
. (22)
Это определяет режущую способность для двухподвесного крепления резцов на диске фрезы.
При этом Wx каната будет равен
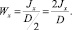 (23)
(23)
Стабилизация рабочего положения резца при резании подтверждена экспериментально при испытании рабочего макета торцевой фрезы диаметром диска 310 мм.
Заключение
Исследованием характеристик подвеса резцов на двух параллельно смещенных канатах показано, что равноопасное сечение по обоим канатам находится в верхней и нижней заделках. Анализ смещения резцов показывает достижение стабилизации их положения при совместном воздействии усилий резания и реакции дорожного покрытия при контакте с дорогой в случае крепления резцов на двух параллельных подвесах. Увеличение смещения при этом не происходит, а действие вертикальной реакции приводит лишь к перераспределению сжимающих и растягивающих усилий в канатах подвеса. Резец претерпевает плоскопараллельное смещение, сохраняя режущее положение относительно плоскости очищаемого дорожного полотна, что подтверждено испытаниями опытного макета торцевой фрезы.



