Работа электрогенерирующего оборудования в энергосистеме РФ регламентирована для следующих основных режимов – первичного регулирования частоты (общего или нормированного) и автоматического вторичного регулирования частоты и перетоков мощности [1, 2]. Причём для небольших (до 100 МВт) объектов электрогенераций (ТЭС, ТЭЦ) главной задачей, как правило, остаётся обеспечение требований к качеству именно вторичного регулирования [3, 4]. Подобные требования (диапазон регулирования, требования к динамике изменения мощности) в большой степени определяют конструктив применяемого электрогенерирующего оборудования, равно как и налагают ограничения на область его применения. В части паровых турбин, как приводных двигателей для электрических генераторов, исследования их динамики и влияния на неё конструктивных параметров ведутся достаточно давно [5, 6] и хорошо систематизированы, особенно для турбин средней и большой мощности (100 и более МВт). Однако и турбины меньшей мощности (с постоянной времени до 10–12 секунд [7]) также остаются хорошим и наглядным объектом для теории автоматического регулирования (ТАР), по которой для обеспечения устойчивой работы с заданным качеством важны и свойства самого объекта, и настройки его регулятора. Обеспечение заданных свойств в части профильного, «целевого» проектирования узлов регулирования и защиты, а также оптимальных настроек регулятора – по-прежнему является нетривиальной нелинейной задачей ТАР, представляющей практический интерес для проектных организаций, о чём свидетельствует большое количество работ по той теме [4, 6, 8].
Цель исследования
Целью настоящей работы явилась выработка практических рекомендаций по определению настройки параметров регулятора в контуре регулирования конкретного объекта. Не рассматривая здесь многокритериальную задачу оптимизации выбранной структуры системы регулирования, остановимся на некоторых практических вопросах её конструирования и настройки. Настоящая работа служит продолжением цикла, посвящённого исследованию быстродействующего прецизионного электромеханического привода, как исполнительного механизма системы регулирования частоты вращения паровой турбины малой мощности [9, 10]. Практический интерес к данному вопросу вызван тем обстоятельством, что большинство паровых турбин Калужского турбинного завода в настоящее время перешло на комплектацию системой регулирования электрогидравлического типа, обладающих рядом эксплуатационных преимуществ по сравнению с прежней гидродинамической системой [11]. Такая система, как правило, состоит из двух функциональных частей: электронной управляющей (ЭУЧ) и гидромеханической исполнительной (ГМЧ), её принципиальная схема показана на рис. 1.
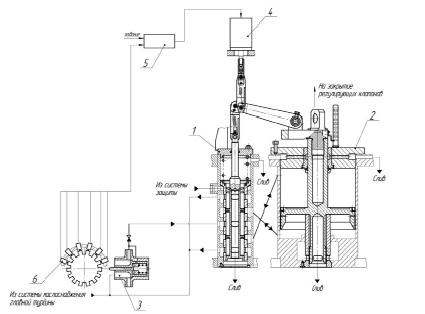
Рис. 1. Принципиальная схема системы регулирования с ЭУЧ ЭГСАР для турбины типа К-17 со следующими условными обозначениями: 1 – отсечной золотник; 2 – сервомотор; 3 – насос-регулятор; 4 – электромеханический преобразователь; 5 – электронное управляющее устройство; 6 – датчик частоты вращения
В состав электронной управляющей части входят (рис. 1):
– электронное управляющее устройство 5;
– электромеханический преобразователь 4;
– шесть датчиков частоты вращения 6.
Материалы и методы исследования
Гидромеханическая исполнительная часть, традиционная для КТЗ, состоит из силовой части – блока регулирования (гидропривод управления положением регулирующего паровпускного клапана турбины) и механической части – парораспределения турбины [7]. В блоке регулирования скомпонованы отсечной золотник (ОЗ) 1 и сервомотор (СМ) 2 – классический следящий гидропривод с перекрёстными обратными связями и управлением СМ по отклонению от нейтрального положения ОЗ [3]. В блоке регулирования масло высокого давления подается от насоса-регулятора 3 на рабочих режимах и от пускового масляного электронасоса в режимах пуска и останова. Давление масла в линии нагнетания насоса-регулятора при номинальной частоте вращения ротора турбины составляет не более 1 МПа.
Теоретические исследования и опыт эксплуатации турбин с системами регулирования типа ЭГСАР (рис. 1) показывают, что для обеспечения требований к качеству процессов регулирования следящий электромеханический привод (ЭМП) отсечного золотника должен обеспечивать высокую скорость перемещения отсечного золотника (до 0,25 м/сек). Ошибка достижения заданного положения отсечного золотника не должна превышать его зоны нечувствительности по гидравлике, обусловленной конструкцией подвижной пары вида «золотник – втулка» (от нескольких сотых до десятых долей мм). Перемещение отсечного золотника с помощью ЭМП должно при этом иметь характер, близкий к монотонному (относительное перерегулирование более 30 % нежелательно с точки зрения потери устойчивости контура регулирования).
Функциональная и структурная схемы блока регулирования гидромеханической части на основе такого ЭМП, полученные на первоначальных этапах исследования [11, 12], показаны на рис. 2 и 3 соответственно.
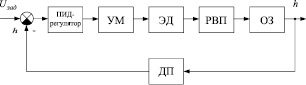
Рис. 2. Функциональная схема блока регулирования с ЭМП и ОЗ, со следующими условными обозначениями: УМ – усилитель мощности; ЭД – электродвигатель; РВП – ролико-винтовая передача; ОЗ – отсечной золотник; ДП – датчик положения
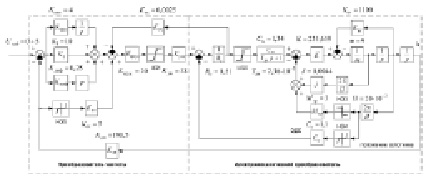
Рис. 3. Структурная схема модели ЭМП с ОЗ (подробности приведены в [12])
В рамках исследования динамики данного контура регулирования модель была упрощена и исследована на устойчивость в области выбранных варьируемых параметров (настройки регулятора), а также выполнена её отработка и частичная верификация по результатам стендовых испытаний опытного образца ЭМП [10], подтвердившая обоснованность базовых параметров модели. На последующем этапе был выполнен анализ результатов выполненных работ. Путем подбора оптимальных значений параметров регулятора из определённой ранее области устойчивости были получены переходные процессы по положению ОЗ с параметрами качества (таблица, строки 1–5), удовлетворяющими требованиям ТЗ на систему регулирования в части времени переходного процесса (tпер) и относительного перерегулирования (σ) [11].
Однако данный результат был получен подбором оптимальных параметров настройки в ручном режиме. Следующей задачей, имеющей более практическую направленность, стало определение оптимальных настроек регулятора данной системы автоматическим путём. Известно, что большинство современных зарубежных промышленных регуляторов для систем автоматического регулирования широкого круга задач уже наделены свойством адаптивности – способности самостоятельно изменять свои настройки под действием внешних факторов, воздействующих на систему, в том числе способных изменять свойства объекта регулирования.
Автоматизированная настройка ПИД-регулятора
Существует множество методов настройки ПИД-регуляторов, в том числе и для сложных, существенно нелинейных объектов управления, таких так турбина со своей системой регулирования скорости вращения. Как правило, при этом стараются придерживаться следующих общих закономерностей:
- увеличение пропорционального коэффициента усиления увеличивает быстродействие и снижает запас устойчивости;
- при уменьшении интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;
- увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие.
Один из способов автоматической настройки параметров ПИД-регулятора, удобный для анализа, реализован в программном обеспечении среды Simulink пакета программ Matlab [13, 14]. Для этого используется встроенный регулятор из библиотеки PID Controller, а также блок Signal Constraint. Их использование применительно к разработанной модели (рис. 3) позволяет добиться получения переходного процесса, близкого к оптимальному, при этом параметры настройки регулятора рассчитываются автоматически методом Монте-Карло. При этом решается так называемая задача сглаживания, для которой критерий оптимизации имеет вид
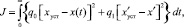 (1)
(1)
где x и x' – значения выходного сигнала и его производной в установившемся режиме (после завершения переходного процесса), q0 и q1 – весовые коэффициенты, которые должны удовлетворять условию
q0 + q1 =1. (2)
На практике вычисления интеграла проводятся на конечном отрезке времени [0; T], который выбирается примерно равным (2 – 3)Tпп (Tпп – время переходного процесса), а если оценить ожидаемое Tпп трудно, то (5 – 6)Ti(max), где Ti(max) – максимальная постоянная времени неизменяемой части системы. Кроме того, вводится нормирующий множитель 1/T, величина xуст заменяется величиной уровня ступенчатого входного сигнала g0, a x'уст = 0.
Таким образом, реально минимизируется функционал
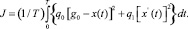 (3)
(3)
Выбор значений весовых коэффициентов q0 и q1 представляет самостоятельную, трудноразрешимую проблему, поэтому на начальных стадиях проектирования полагают q0 = q1 = 0,5.
Следует отметить, что выбор метода решения может быть изменён программными настройками пакета (доступны также методы Рунге – Кутта, Зиглера – Никольса, Стогестада, Шеделя и др.), в данном случае при выборе руководствовались практическими рекомендациями работы В.А. Жмудь [15].
Результаты исследования и их обсуждение
Переходные процессы по положению выходного штока ЭМП в исследуемом контуре при различных вариантах настройки представлены на рис. 4.
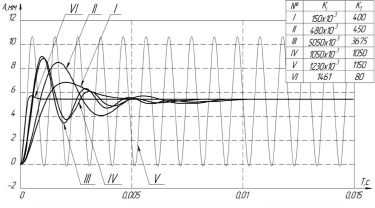
Рис. 4. Сравнительный анализ двух методов настройки регулятора с учетом внесенных изменений
Ниже приведена таблица со значениями коэффициентов настройки регулятора вручную (№ 1–5) и автоматическим методом (№ 6).
Параметры качества переходных процессов ЭМП с ОЗ
|
№ п/п |
Кинт |
К1 |
tпер, сек |
σ, % |
|
1 |
1,5•105 |
400 |
0,045 |
30 |
|
2 |
4,8•105 |
450 |
0,06 |
61 |
|
3 |
1,23•106 |
1 150 |
0,05 |
71 |
|
4 |
1,05•106 |
1 050 |
0,05 |
61 |
|
5 |
5,05•106 |
3 675 |
--- |
--- |
|
6 |
9426 |
224 |
0,01 |
6,25 |
Выводы
Проанализировав результаты сравнения переходных процессов, можно полагать, что метод автоматизированной настройки, базирующийся на методе Монте-Карло, более удобен и универсален для контуров регулирования данного типа, нежели подбор их параметров вручную.



