Рост установленной мощности нелинейных резкопеременных нагрузок в автономных системах приводит в ряде случаев к ухудшению показателей качества электроэнергии.
Искажения синусоидальности кривых напряжений и токов вызываются работой электроприборов с нелинейной вольтамперной характеристикой и регулируемых преобразователей переменного тока в постоянный. Кривые тока и напряжения в этих случаях приобретают вид, отличный от синусоиды.
Первым проявлением низкого качества электроэнергии являются искажения формы синусоидального напряжения в цепях питания, отклонения напряжения за пределы установленных допусков или полные прерывания подачи электроэнергии. Эти возмущения могут быть вызваны гармониками сетевой частоты или неполадками в системе электроснабжения. Они могут длиться от миллисекунд до секунд. Внешние возмущения обычно проявляются как неправильная работа оборудования или его полная остановка [1, 2].
В последнее время возник большой интерес в области разработки активных фильтров сетевой частоты, позволяющих компенсировать влияния высших гармоник, для улучшения качества электроэнергии.
При активной фильтрации основной задачей является разработка эффективного метода идентификации (выделение) кондуктивных помех в электрической сети. Устройство управления обеспечивает формирование соответствующих управляющих сигналов, под воздействием которых широтно-импульсный модулятор активного компенсатора генерирует компенсирующий сигнал.
Отклонения напряжения от номинальных значений, колебания напряжения и частоты, искажения симметрии и синусоидальности напряжений приводят к ряду нежелательных явлений. Увеличиваются потери электроэнергии в сетях и в электрооборудовании. Увеличение потерь электроэнергии в оборудовании вызывает дополнительный его нагрев, что приводит к сокращению сроков службы оборудования или необходимости увеличения его мощности.
Разработан активный компенсатор кондуктивных помех для электроэнергетической системы с идентификацией структурных составляющих в ортогональном вейвлет-базисе.
Научная новизна работы заключается в разработке методики выделении опорной частоты кривой тока (напряжения), а также компенсирующего сигнала помехи сети электропитания с применением вейвлет-преобразования.
Материалы и методы исследования
Сигналы сети электропитания (напряжение) содержат разномасштабные локальные возмущения. Временная протяженность и величина особенностей зависит от природы возмущений.
Для представления сигналов с локальными особенностями удобным и информативным является способ построения нелинейных аппроксимирующих схем с применением адаптивных фильтров. Наиболее эффективным методом реализации данной процедуры является вейвлет-анализ.
Экспериментальные исследования показали эффективность применения вейвлет анализа для создания активного компенсатора кондуктивных помех в системах электроснабжения.
Применение разработанного активного компенсатора помех питающего напряжения дает возможность в режиме реального времени компенсировать помехи, вызванные применением электрооборудования с нелинейными вольт-амперными характеристиками, тем самым улучшить качество электроэнергии в системах электроснабжения [3].
Наличие высших гармонических составляющих в токах нелинейных электропотребителей приводит к разрушительным последствиям.
1. Импульсный характер нагрузки приводит к деформации синусоиды напряжения, действующей на зажимах нагрузки.
2. Нелинейные нагрузки генерируют высочастотные гармоники тока, что вызывает дополнительные потери в обмотках трансформатора. Так, для линейных нагрузок потери на вихревые токи составляют в общих потерях приблизительно 5 %, а с нелинейной нагрузкой они возрастают до 75 % [4].
3. Высшие гармоники напряжения уменьшают емкостное сопротивление компенсирующих конденсаторов. Напряжения высших гармоник вызывают значительные токи гармоник, что приводит к скорому старению изоляции и возникновению перегрузки по току.
4. Высшие гармоники ухудшают механические характеристики и КПД синхронных и асинхронных машин. Ускоряют старение изоляции электрических машин, кабелей и трансформаторов [4].
5. Под воздействием высших гармоник нарушается работа устройств электронной автоматики [5].
Электроэнергетическая система является системой со сложной электромагнитной обстановкой, в которой существуют различного вида помехи, воздействующие на цепи питания.
Для анализа структуры сигнала сети разной длительности необходимы частотно-временные составляющие с различными временными характеристиками.
Ортонормированные вейвлеты являются носителями подробностей, необходимых для повышения разрешения аппроксимации сигнала.
Свойство частотной и временной локализации вейвлет-функций может быть охарактеризовано концентрацией их энергии в частотной и временной областях, или посредством частотно-временных окон [6].
На базе процедур вейвлет-анализа разработана методика фильтрации сигнала питающего напряжения, для обеспечения качественного подавления интергармонических составляющих и импульсных помех [7].
Вейвлет-функция может описывать сложный сигнал во временном и частотном представлении с большой точностью.
Определим требования к вейвлет-базису:
– максимально точное выделение основной гармоники 50 Гц, а также высших гармонических составляющих;
– оптимальное количество уровней детализации вейвлет-дерева;
– минимальная длина вейвлет-разложения.
Важной задачей является выбор вейвлет-фильтра, позволяющего максимально точно восстанавливать сигнал сети после прямого и обратного вейвлет-разложения.
В теории вейвлет-анализа существует большое число различных семейств базисных вейвлет-функций.
Важным свойством базисных функций является свойство ортогональности. Оно обеспечивает представление функции f в виде суммы ортогональных компонент:
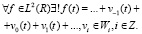
Основной принцип работы алгоритма вейвлет-преобразования сетевых сигналов состоит в разложении приближения сигнала на две компоненты: аппроксимирующую и детализирующую, а также их дальнейшее дробление для увеличения уровня декомпозиции сигнала. Этот алгоритм работает как во временной, так и в частотной областях.
Вейвлет Добеши является ортогональным и имеет минимальный компактный носитель при заданном числе нулевых моментов. С возрастанием числа нулевых моментов возрастает гладкость вейвлета, что способствует более четкому представлению детализирующих компонентов сигнала.
Вейвлеты Добеши вычисляются с помощью сопряженных зеркальных фильтров для конечных импульсных откликов h, где h есть тригонометрический многочлен [6]:
.
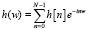Численные методы построения аппроксимирующей схемы построим на основе алгоритма:
1) очистка от шума с помощью пороговой функции и с применением вейвлет-пакета;
2) определение критериев выбора вейвлет-базиса, выделение информативных ветвей дерева, формирование структуры лучшего дерева аппроксимации (рис. 1);
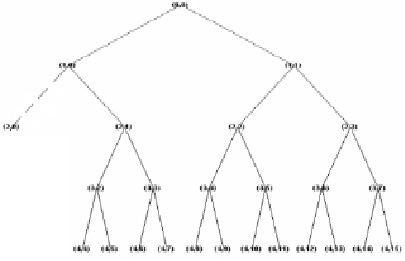
Рис. 1. Выделение информативных ветвей дерева вейвлет-разложения по базису db4
3) идентификация локальных особенностей сигнала тока на основе лучшего дерева вейвлет-разложения по базису [3].
Процедура определения структуры дерева разложения для конкретного сигнала может быть выполнена путем реализации следующего рекурсивного алгоритма:
1) разложение сигнала сети в базисе вейвлет-дерева: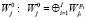 
, 
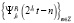есть базис пространства 
;
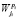2) выбор информативных ветвей дерева, определяющих структурные компоненты сигнала сети, где наилучший базис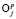 
пространства 
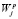есть базис
,
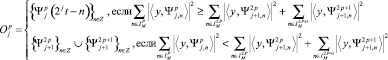где множества индексов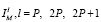 
определяются как
индекс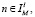 
если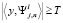 
, где порог 
.
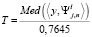Назовем этот алгоритм алгоритмом идентификации структурных компонентов сигнала [7].
Результаты исследования и их обсуждение
С целью проверки выдвинутых положений проведем компьютерный модельный эксперимент с применением Matlab Wavelet Toolbox и графической среды имитационного моделирования Simulink [8].
В качестве эталонного сигнала для фильтрации определим модельный сигнал с импульсными помехами 100 В, моделирование производится в течение 3 с, с частотой дискретизации 2 кГц, фрагмент сигнала представлен на рис. 2. При обработке сигналов в среде Matlab применялись вейвлеты Добеши 4 (db4) [9].
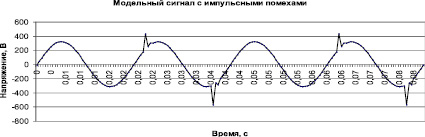
Рис. 2. Модельный сигнал с импульсными помехами
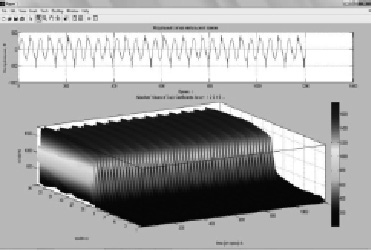
Рис. 3. Вейвлет-спектр модельного сигнала с импульсными помехами
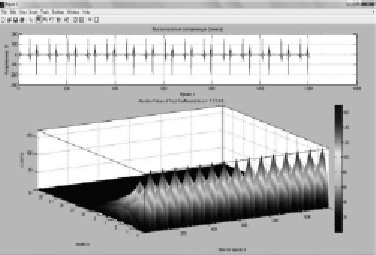
Рис. 4. Вейвлет-спектр с импульсными помехами (выделенная высокочастотная составляющая сигнала)
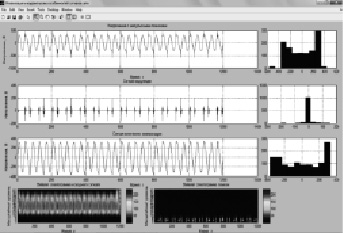
Рис. 5. Компенсация импульсных помех с применением вейвлет-анализа
Рис. 6. Принцип работы системы управления вейвлет-фильтрацией и прогнозом искажений [11]
Рассмотрим подробнее разложение модельного сигнала по вейвлет-дереву (рис. 1). На первом уровне разложения аппроксимация сигнала (1,0) отображает сигнал сети, здесь присутствуют основная частота и помеха, детализирующая ветка (1,1) состоит из высокочастотных колебаний, амплитуда помехи на два порядка меньше, чем амплитуда аппроксимации. На втором уровне разложения вейвлет-дерева осуществляется разделение крупномасштабной (2,0) и мелкомасштабной (2,1), (2,2), (2,3) составляющей сигнала сети.
Анализ сигнала (рис. 3, 4) показывает наличие широкого спектра гармонических составляющих. На рис. 4 отчетливо виден ряд максимумов сигнала сети. На рис. 3, 4 представлено трехмерное пространственное изображение спектра сигнала сети после вейвлет-преобразования, которое наглядно показывает изменение таких параметров, как, амплитуда, частота и время.
На рис. 5 представлены результаты компенсации импульсных помех с помощью представленных алгоритмов [10].
Принцип работы системы управления вейвлет-фильтрацией и прогнозом искажений представлен на рис. 6.
Применение разработанного комплекса программ обнаружения нарушений показателей качества электрической энергии во время мониторинга позволяет контролировать качество электрической энергии в режиме реального времени. Отсутствует необходимость сбора статистических данных, разработанные методы позволяют своевременно применять алгоритм улучшения качества электрической энергии.
Заключение
В статье представлено решение комплекса задач, направленных на повышение качества электроэнергии в электроэнергетических системах. В результате проведенных исследований разработано математическое и программное обеспечение активного компенсатора кондуктивных помех в ЭЭС.
Полученные результаты:
1. Экспериментально доказано, что наиболее опасными являются широкополосные импульсные помехи с апериодической составляющей.
2. При сравнении алгоритмов активной фильтрации установлено, что применение Фурье базиса требует высокого порядка фильтра, что приводит к значительной фазовой задержке и погрешности. Произведен выбор вейвлет-базисов для более эффективной идентификации структурных составляющих сигналов питающего напряжения.
3. Разработаны алгоритмы и методика идентификации структурных составляющих несинусоидальных сигналов сети (напряжения и тока) в электроэнергетической системе с применением ортогональных вейвлет-базисов Добеши.