В настоящее время в телекоммуникационных системах широко применяется технология, которая базируется на ортогональном частотном мультиплексировании OFDM (Orthogonal Frequency Division Multiplexing) [1–3]. Это связано с необходимостью обеспечения высокоскоростной передачи мультимедийных данных в системах беспроводной связи. Кроме этого, технология OFDM обладает целым рядом достоинств, среди которых можно выделить: высокую спектральную эффективность, эффективную работу в условиях многолучевого распространения сигналов; высокую устойчивость к узкополосной интерференции, которая способна исказить небольшую часть поднесущих [1]. Однако применение в системах OFDM быстрых преобразований Фурье (БПФ) приводит к недостаткам, среди которых можно отметить наличие двух вычислительных трактов, накопление ошибок округления. Кроме того, при выполнении обратного быстрого преобразования Фурье (ОБПФ) в передатчике и БПФ в приемнике используются матрицы поворачивающих коэффициентов, в которых отсутствуют нулевые элементы. Это приводит к тому, что искажение одного разряда в сигнале OFDM при передаче в канале связи приведет к размножению ошибки при восстановлении сигнала. То есть на приеме будут искажены N отсчетов после выполнения БПФ, где N – число поднесущих в сигнале OFDM.
Устранить данный недостаток возможно за счет использования ортогональных преобразований сигналов, прямая матрица которых содержит нулевые элементы. Этому требованию удовлетворяют дискретные вейвлет-преобразования. Повысить эффективность выполнения ДВП можно за счет использования модулярных кодов. Поэтому реализация технологии OFDM на основе дискретных вейвлет-преобразований, использующих модулярные коды, применение которых позволит повысить помехоустойчивость системы с ортогональным частотным мультиплексированием, является актуальной задачей.
Цель исследования
Современные системы OFDM не позволяют обеспечить максимальную помехоустойчивость, так как при выполнении ОБПФ на передающей стороне и БПФ используются матрицы, которые содержат N2 ненулевых поворачивающих коэффициентов, где N – число поднесущих в сигнале OFDM. В результате этого в системах OFDM наблюдается эффект размножения ошибок, когда искажение одного бита передаваемых данных приводит к искажению N отсчетов на приеме после выполнения БПФ. Устранить данный недостаток возможно, если в системах OFDM в качестве ортогонального базиса будут использованы ДВП, реализованные в модулярных кодах. Поэтому целью статьи является повышение помехоустойчивости системы OFDM за счет использования нового базиса – ДВП, выполняемого в МК.
Материалы и методы исследования
В процессе развития сетей передачи данных, в том числе и беспроводных, постоянно увеличиваются требования к скорости передачи информации и качеству предоставляемых сервисов. Одним из перспективных видов сигнально-кодовых конструкций является ортогональное частотное мультиплексирование OFDM (Orthogonal Frequency Division Multiplexing). При использовании данной технологии поток входных данных s(n) разбивается на множество параллельных потоков, каждый из которых передается с помощью соответствующей несущей. В результате этого высокоскоростной последовательный цифровой поток заменяется множеством низкоскоростных потоков. Основная идея метода OFDM заключается в расположении набора «независимых» подканалов таким образом, чтобы, с одной стороны, один подканал не являлся помехой другому, а с другой стороны, спектры подканалов перекрывались. Для выполнения данного условия в OFDM предлагается использовать дискретное преобразование Фурье (ДПФ), реализованное на основе быстрых алгоритмов БПФ. Рассмотрим дискретную модель системы с OFDM на основе ДПФ, приведенную в [4]. Такая модель на передающей стороне выполняет операцию ОДПФ с последующим добавлением циклического префикса (ЦП), а на приемной стороне – дискретное преобразование Фурье с использованием быстрых алгоритмов вычислений. На рис. 1 приведена дискретная модель системы с OFDM.
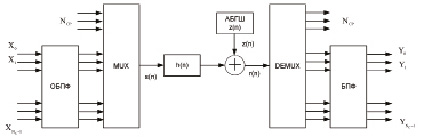
Рис. 1. Дискретная модель системы с OFDM на основе БПФ
На передающей стороне системы с OFDM поток битов разбивается на блоки, содержащих NC двоичных символов. Эти блоки образуют вектор данных, который можно представить в виде X = (X0, X1, …, XNc-1)T. Затем данный вектор подвергается обратному быстрому преобразованию Фурье. А затем к нему добавляют циклический префикс длиной NСР. Тогда результирующий комплексный низкочастотный сигнал имеет вид
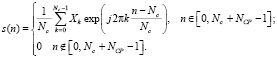(1)
Полученный сигнал s(n) поступает на вход линейного стационарного дискретного канала (ДК) h(n). При прохождении по данному каналу на сигнал s(n) воздействует аддитивный белый гауссовский шум (АБГШ) z(n). Такой шум характеризуется нулевым средним и дисперсией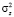 
. При этом полагаем, что между передающей стороной и приемной стороной обеспечивается идеальная синхронизация. При выполнении отмеченных условий на приемной стороне будет принят сигнал
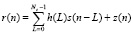. (2)
После этого из принятого сигнала удаляют циклический префикс, а затем осуществляют выполнение ДПФ. В этом случае имеем
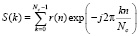. (3)
После выполнения БПФ на выходе приемника будет получен сигнал
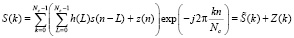, (4)
где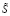 
– идеальный сигнал; Z(k) – шум в дискретном канале.
Использование в OFDM быстрых алгоритмов ДПФ Фурье позволило обеспечить высокую скорость передачи сигналов и спектральную эффективность. Кроме того, технология OFDM характеризуется эффективной работой в условиях многолучевого распространения сигналов, а также высокой устойчивостью к узкополосной интерференции, которая способна исказить небольшую часть поднесущих [4].
Однако ДПФ и ОБПФ выполняются в поле комплексных чисел, что приводит к увеличению схемных затрат. Это связано с необходимостью применять два вычислительных тракта для обработки действительной и мнимой части сигнала. Кроме того, в качестве поворачивающих коэффициентов БПФ и ОБПФ используются тригонометрические функции, которые являются иррациональными числами, что приводит к накоплению ошибок округления [5]. Наряду с отмеченными недостатками системы с OFDM, использующие ДПФ, не обладают максимальной помехоустойчивостью. Проведенные исследования показали, что искажение одного разряда в сигнале OFDM при передаче в канале связи из-за помех приведет к размножению ошибки при восстановлении сигнала. Это связано с тем, что математическая модель ортогональных преобразований сигналов на основе БПФ и ОБПФ использует прямую и обратную матрицу, в которой отсутствуют нулевые элементы. Рассмотрим выполнение ДПФ для входного вектора из N = 8 отсчетов. Тогда имеем
, (5)
где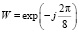 
– дискретная экспоненциальная функция.
Используя выражение (5), получаем следующие спектральные составляющие:
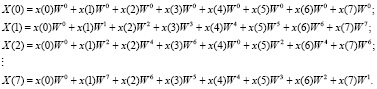(6)
Анализ выражения (6) показывает, что в получении каждой составляющей спектрального отсчета X(j) используются все временные отсчеты, поступающие из канала связи, от х(0) до х(7). Из представленных вычислений наглядно видно, что при искажении бита, например в нулевом отсчете х(0), на приеме после выполнения БПФ будут искажены все N отсчетов спектра сигнала, где N – число поднесущих в сигнале OFDM.
Повысить помехоустойчивость системы OFDM можно за счет использования дискретных вейвлет-преобразований. Если в технологии OFDM заменить ортогональные преобразования, выполняемые в поле комплексных чисел, на ДВП, то дискретная модель системы с OFDM будет иметь вид, показанный на рис. 2.
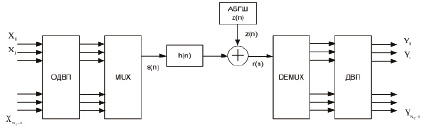
Рис. 2. Дискретная модель системы с OFDM на основе ДВП
При этом для повышения эффективности реализаций ДВП сигнала воспользуемся модулярными кодами. Применение МК позволяет повысить скорость вычислений за счет распараллеливания на уровне арифметических операций и использования малоразрядных остатков, а также обеспечить максимальную точность результатов [6–8]. В качестве ДВП выберем Добеши 4, которое реализуется по модулю pi, где i = 1, 2, .., k, и осуществим прямое преобразование для N = 8 отсчетов. Тогда получаем
, (7)
где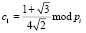 
; 
; 
; 
; 
; 
.
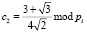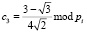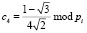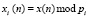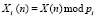Тогда получаем следующие аппроксимирующие и детализирующие коэффициенты:
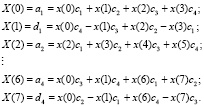(8)
Анализ выражения (8) показывает, что для получения первого сглаживающего коэффициента ДВП а1 используются четыре отсчета от х(0) до х(3), поступившие из канала связи. Если в процессе передачи исказится нулевой отсчет нулевой х(0), то согласно (6) будут искажены два сглаживающих коэффициента а1 и а4, а также два детализирующих коэффициента d1 и d4. Остальные сглаживающие и детализирующие коэффициенты останутся без изменений.
Результаты исследования и их обсуждение
Для оценки помехоустойчивости систем с OFDM были использованы дискретные модели систем с ортогональным частотным мультиплексированием, использующие ортогональные преобразования ДПФ и Добеши-4, представленные в МК. В качестве оснований МК были выбраны модули р1 = 23, р2 = 47, р3 = 71. Диапазон модулярного кода Рраб = 76751. Для моделирования входного потока данных генерировалась бинарная псевдослучайная последовательность. Из данной ПСП формировался набор модуляционных символов 64 отсчета размерности по 8 бит каждый. Формирование происходило в одинаковой полосе частот (20 МГц) и с равной длительностью (12,8 мкс). Генерировался аддитивный гауссовский шум, который умножался на нормирующий коэффициент для соответствия заданному уровню мощности, а затем складывался с каждым из сформированных сигналов. Полученные сигналы демодулировались, а затем вычислялось отношение ошибочно принятых бит Lош к общему количеству переданных L согласно
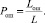(9)
Для обеспечения точности Рош(BER) выполнялось условие L ≥ 106 и результаты усреднялись по серии из 5 экспериментов. Результаты представлены на рис. 3.
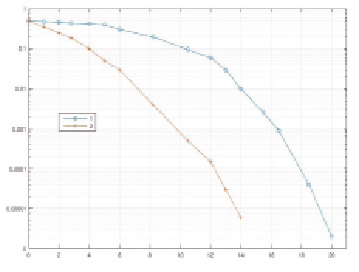
Рис. 3. Кривые помехоустойчивости систем OFDM, построенных на основе ДПФ и ДВП Добеши-4, реализованных в МК (1 – OFDM на основе БПФ, 2 – OFDM на основе ДВП в МК)
Приведенные результаты моделирования показали, что использование дискретных вейвлет-преобразований, реализованных в МК, позволяет повысить помехоустойчивость систем OFDM по сравнению с ортогональными преобразованиями ДПФ. Так, при отношении сигнал/шум равном 4 дБ вероятность ошибки системы OFDM на основе ДПФ составляет Рош = 0,41. При этом при использовании ДВП Добеши-4, реализованного в модулярном коде, обеспечивает вероятность ошибки Рош = 0,1. Для достижения вероятности ошибки равной Рош = 10-5 в системах OFDM на основе ДПФ необходимо обеспечить отношение сигнал/шум равный 19дБ, а при использовании разработанного алгоритма реализации ДВП в модулярном коде – потребуется 13,5 дБ. Таким образом, интеграция свойств модулярных кодов и дискретных вейвлет-преобразований позволяет повысить помехоустойчивость при выполнении ортогонального частотного мультиплексирования сигналов.
Заключение
В статье представлена модель системы OFDM, использующая в качестве ортогональных преобразований дискретные вейвлет-преобразования, реализованные в модулярных кодах. Приведенные результаты моделирования показали, что использование ДВП, реализованных в МК, повышает помехоустойчивость систем OFDM по сравнению с ортогональными преобразованиями ДПФ. Так, при отношении сигнал/шум равному 4 дБ вероятность ошибки системы OFDM на основе ДПФ составляет Рош = 0,41. При этом при использовании ДВП Добеши-4, реализованного в модулярном коде, обеспечивает вероятность ошибки Рош = 0,1. Для достижения вероятности ошибки равной Рош = 10-5 в системах OFDM на основе ДПФ необходимо обеспечить отношение сигнал/шум равный 19 дБ, а при использовании разработанного алгоритма реализации ДВП в модулярном коде – потребуется 13,5 дБ. К перспективным направлениям применения целочисленных ДВП в системах OFDM можно отнести способность модулярных кодов обнаруживать и корректировать ошибки, возникающие в процессе вычислений. Использование избыточных МК позволит повысить отказоустойчивость систем OFDM, построенных на основе ДВП.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 17-37-50009.