Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

На сегодняшний день АОС становятся неотъемлемой частью современных образовательных процессов в системе высшего образования. Специфика методов обработки информации в АОС связана, прежде всего, с тем, что современные автоматизированные обучающие системы представляют собой интеллектуальные системы, построенные на основе парадигмы обработки баз знаний (БЗ). В этом ключе, говоря об информации, мы далее будем иметь в виду знания, и наоборот, говоря о знании, будем иметь в виду информацию. Статья посвящена аналитическому обзору методов представления информации.

Под методами представления информации мы будем понимать способ формального описания информации и оперирования этими описаниями.

Основой классификации методов представления информации являются модели их представления в БЗ. На сегодняшний день существуют различные классификации моделей знаний. В [1]: продукционные модели, фреймы, формально-логические модели, модели на основе онтологии, включая семантические сети, другие модели (комбинированная, модель в виде И-ИЛИ дерева, модель в виде дерева понятий, UML-модель); [2]: логические, продукционные, фреймовые, сетевые, объектно-ориентированные, специальные и комплексные; [3]: логическая, продукционная, фреймовая, сетевая, другие модели (объектно-ориентированные, специальные и комплексные); [4]: на основе исчисления высказываний и исчисления предикатов, продукционные, семантические, фреймовые, интегрированные; [5–7]: логическая, продукционные, фреймы, нейронные сети, гибридные модели и т.д. В силу большого разнообразия моделей представления информации в первой части статьи ограничимся рассмотрением методов продукционной и логической моделей представления информации.

Продукционная модель. Описана в [8, 9]. Основу представления знаний составляют системы продукций, каждая продукция имеет вид «если А, то В», где А – факт (понятие), В – действие. Интерпретируется двумя способами: если посылка А истинна, то действия, указанные в части ТО, выполняются; вероятностная интерпретация, при которой правило «если А, то В» срабатывает с некой вероятностью, зависящей от истинности посылки А. Под действием обычно понимается операция добавления факта в БЗ интеллектуальной системы или взаимодействие с внешней средой.

Такая система позволяет представить виды знаний, описывающие: понятия (факты) ПО, причинно-следственную связь понятий (фактов) А и В; некоторые действия А и В; знания (А) и действия (В). Примеры, демонстрирующие указанные виды знаний: «если число делится на два, то оно – четное», «для того, чтобы вычислить значение производной в точке х с помощью графика, проведём в этой точке касательную к графику функции», «если в условии задачи указано, что дан график производной функции, то можно определить знаки производной функции в точке». Для представления нечетких знаний А и В снабжаются коэффициентами достоверности (или уверенности), которые могут принимать значения из разных интервалов в разных системах, например [0,1]. К методам представления продукционной модели знаний относится метод формализации знаний в форме правил, структурированных в общем виде как: ЕСЛИ А1, А2, …, Аn, то В, где Аi связаны логическими операциями «И», «ИЛИ», «НЕ». Суть метода: «Сопоставить – выполнить». Пример представления знаний этим методом:

Посылки «Образование – Высшее» и «Возраст < 35» записаны в БЗ.

ПРАВИЛО 1:

ЕСЛИ

Образование – Высшее И

Возраст – Молодой

ТО

Шансы найти работу > 0,8.

ПРАВИЛО 2

ЕСЛИ

Возраст < 35

ТО

Возраст – Молодой

Так как посылки «Образование – Высшее» и «Возраст < 35» существуют в БЗ, а посылка «Возраст – Молодой» – отсутствует, то в БЗ помещается факт из условной части правила 2 «Возраст – Молодой». При повторном применении правил правило 2 уже не используется, так как было применено, а правило 1 становится истинным и в БЗ помещается факт «Шансы найти работу > 0,8».

Возможна и обратная ситуация.

Анализ механизмов метода представления информации в форме правил позволил нам выявить ряд ограничений на представляемую этим методом информацию.

Однозначность. Нельзя представить этим методом многозначные или неточные понятия. Например, понятие «оператор»:

ПРАВИЛО 1:

ЕСЛИ Оператор

ТО Юридическое лицо

ПРАВИЛО 2:

ЕСЛИ Оператор

ТО Управляет техническим устройством

ПРАВИЛО 3:

ЕСЛИ Оператор

ТО Практикующий хирург

При попытках сопоставления условной части каждое из правил будет истинным. Для механизма метода это означает ситуацию «конфликта выполнения» заключительной части правила.

Возможна другая ситуация. Представляемая информация однозначна, но имеется несколько правил выполнения результирующей части.

Дополним пример представления знаний этим методом правилом 3.

ПРАВИЛО 3:

ЕСЛИ

Образование – Высшее

ТО

Можно поступить в аспирантуру.

В результате добавления правила 3 появляется возможность применения на одном шаге работы метода и правила 2 и правила 3. Возникает ситуация «конфликта набора правил». Применение правила 2 на первом шаге дает возможность применить на втором шаге и правило 1 и правило 3. Если применить правило 1, то в БЗ будет помещен факт «Шансы найти работу > 0,8». Если же вначале применить правило 3, то в БЗ будет помещен факт «Можно поступить в аспирантуру», а затем, после применения правила 1, факт «Шансы найти работу > 0,8». Налицо временная зависимость скорости работы метода от количества правил и порядка выполнения правил.

Принцип сопоставления информации, лежащий в основе метода, требует:

- однородности (однотипности, одинаковости) представляемой информации;

- одинакового синтаксиса описания представляемой информации;

- обязательного наличия в БЗ информации, выступающей посылкой, в момент использования правила.

Логическая [8, 9] или, в трактовке [1], формально-логическая модель. Знания ПО представляются в виде предикатов – логических функций F(x1,x2,...,xm), принимающих значение ИСТИНА или ЛОЖЬ, где F – имя предиката, xi – аргументы предиката. Каждый предикат структурно состоит из элементарных составляющих, в качестве которых могут выступать другие предикаты или логические функции f(x1, x2, ..., xm), записанные с использованием логических связок «И», «ИЛИ», «НЕ», «СЛЕДОВАНИЕ» и кванторов всеобщности (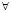) и существования ().

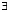Так же как и в продукционной модели, информация представляется в форме совокупности правил, записанных в виде логических формул, что накладывает аналогичные ограничения на представляемую информацию. Отличием является то, что правила не имеют форму продукций, а представляют собой понятия (факты или утверждения) и отношения между ними.

Примером представления знаний с помощью этой модели служит предикат «образование (среднее, специальное, высшее)». Может обозначать понятие «образование» как отношение, связывающее между собой уровни образования. А может обозначать свойство объектов-аргументов (среднее, специальное, высшее), обозначенных именем предиката «образование». К логическим методам представления знаний ПО можно отнести: исчисление высказываний 1-го порядка (логика предикатов), метод резолюции, методы модальных логик.

Рассмотрим указанные логические методы.

Метод исчисления высказываний 1-го порядка. Суть метода: вычисление заключения из предикатов. Ограничение: нельзя использовать в качестве аргументов предиката логическое выражение, т.е. представляемая информация должна обладать свойством высокой структурированности.

Рассмотрим наш пример с поиском работы. Исходные посылки «Образование – Высшее», «Возраст < 35» и «Шанс найти работу > 0,8» разложатся на элементарные части. «Образование» – субъект, «высшее» – свойство субъекта. Таким образом, «образование» является предикатом, например, р, свойство «высшее» – одно из возможных значений аргумента предиката р. Более общая запись будет иметь вид р(х). Соответственно, свойство «Возраст < 35» – предикат q(y), где у – возможные значения предиката «Возраст», «Шанс найти работу» – предикат а(k), где k – возможные значения вероятности найти работу.

Тогда информация, содержащаяся в утверждениях, будет представлена в виде: 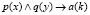. В отличие от продукционного метода не требуется вначале установить истинность p, а затем истинность q. а истинно, если p и q истинны, то есть вычисление заключения происходит вне зависимости от порядка обработки условий p и q.

Метод резолюции представляет собой более фундаментальную формализацию по сравнению с методом логики предикатов. Указанное отличие предполагает перед переходом к заключению приведение изначально заданных логических формул к определенной нормальной форме, например префиксной нормальной форме (ПНФ). Преобразование основывается на ряде правил: выведение кванторов 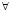и 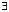перед логической формулой, исключение связок 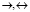путем их замены на связки И, ИЛИ, НЕ, полное исключение кванторов 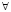и 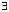из формулы.

Пример представления информации этим методом: 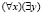РАВНО (X, Y) – «для каждого х существует y, такой, что х равно y». Указанное соотношение позволяет заменить у на функцию f(х), описывающее данное отношение. Учитывая тот факт, что функция f(х) возникла потому, что переменная у проквантифицирована квантором 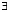, полученная логическая формула примет вид: 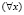РАВНО (x, y).

Методы модальной логики описаны в [10–12] являются расширением логики предикатов 1-ого порядка, за счет введения возможности качественной оценки связи, установленной в высказывании, с помощью аппарата многозначных логик:

- модальных операторов, например, «возможно», не принимающего значение ИСТИНА или ЛОЖЬ, а принимающего некое третье значение (трехзначная логика Лукасевича);

- четырехзначная логика (истинно и неложно, ложно и неистинно, истинно и ложно, ни истинно и ни ложно – 1, ‘+’, ‘–‘, 0 соответственно);

- аксиом, выражающих условия истинности, о замене эквивалентным и т.д.

Используются для представления в БЗ противоречивой и неполной информации, т.е. являющейся истинной и ложной или ни истинной и ни ложной. Примером представления информации с помощью модальной логики является запись утверждения «Возможно, завтра пойдет дождь» вида: ∇(х), где символ ∇ – обозначение модального оператора «возможно», х – утверждение «завтра пойдет дождь». Это утверждение не является сегодня ни истинным, ни ложным, оно имеет некое третье значение, именуемое «возможность» и обозначаемое, например, 1/2 [11].

Таким образом, появляется возможность представить информацию не только о реальном, но и возможном (или необходимом) событии (явлении, объекте, свойстве и т.п.).

Возможны другие модальные операторы – «необходимо», «всегда» и т.д. – и соответствующие модальные логики. Виды модальных логик представлены, например, в [3]. Следуя [3], перечислим наиболее известные: алетическая логика (модальности «возможно – необходимо»), деонтическая логика (модальности «разрешено – обязательно»), эпистемическая логика (логика «знания – веры»), временная модальная логика (модальности «всегда – никогда», «часто – иногда»).

Псевдофизические логики объединяют в себе целый класс методов: пространственная и временная логики, логика оценки величин, логика действий. Методы представлены в [13,14]. Целью перечисленных методов является формализация нестрогих рассуждений человека о рассматриваемой предметной области в виде так называемых лингвистических переменных, генерация на основе правил вывода новых знаний о данной области, пополнение новыми знаниями БЗ. Значения лингвистических переменных связаны со значениями различного рода шкал: возраста (количество лет), расстояния (м или км) и т.д. Например, со значениями шкалы «возраст» можно связать соответственно значения лингвистической переменной: «юный», «молодой», «зрелый», «старый» или диапазоны значений шкалы: «0 … 17», «17 ... 21», «22 … 35», «36 … 50» и т.д.. Таким образом устанавливается связь между разнотипной информацией. Как следствие, метод дает возможность установить связь и единовременно представить разнотипную информацию. Такого рода взаимосвязи образуют базовые отношения, из которых с помощью логических связок строятся производные отношения. Примером представления информации методом псевдофизических логик является понятие «пожилой» как конъюнкция от понятий «зрелый» и не «старый» и возраст «от 22 до 35 лет».

Результаты обзора методов продукционной и логической моделей представления информации сведены в таблице.