Для снижения стоимости добычи и транспортировки углеводородов из Арктики широко применяются автоматизированные системы дистанционного контроля и управления объектами нефтедобычи. Для организации связи между необслуживаемыми объектами и центром управления используются низкоорбитальные системы спутниковой связи (ССС). С целью противодействия навязывания ретрансляционной помехи спутником-нарушителем, которая имитирует команду управления, в работах [1] предлагается использовать запросно-ответную систему распознавания спутника (ЗОСРС). Очевидно, что имитостойкость такой системы во многом зависит от протокола аутентификации. Как правило, такие протоколы типа «запрос – ответ», базирующиеся на доказательстве с нулевым разглашением знаний (ДНРЗ), реализуются по большому модулю, что негативно сказывается на скорости аутентификации. Снизить временные затраты на проверку статуса спутника можно за счет применения модулярных кодов (МК). Поэтому реализация протоколов аутентификации с доказательством нулевого разглашения знаний с использованием модулярных кодов является актуальной задачей.
Цель исследования
Для повышения имитостойкости запросно-ответной системы распознавания спутника применяются протоколы, базирующиеся на доказательстве с нулевым разглашением знаний. С целью повышения криптостойкости в таких протоколах используются большие числа. Однако увеличение разрядности обрабатываемых данных приводит к снижению скорости выполнения мультипликативных операций. Применение непозиционных МК позволяет не только повысить точность, но и скорость вычислений. Это обусловлено тем, что в этих кодах операнды – это остатки, полученные по модулям МК. А операции сложения, вычитания и умножения выполняются параллельно без обмена данными между разными модулями [2–4]. Поэтому целью работы является повышение скорости выполнения протокола аутентификации за счет использования модулярных кодов.
Материалы и методы исследования
К модулярным кодам относятся непозиционные коды, в которых число А представляется в виде остатков 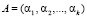 , где
, где 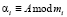 , mi – основания МК, в качестве которых используют взаимно простые целые числа, i = 1, 2,…, k [2–4]. Тогда для МК справедливы следующие выражения
, mi – основания МК, в качестве которых используют взаимно простые целые числа, i = 1, 2,…, k [2–4]. Тогда для МК справедливы следующие выражения
 , (1)
, (1)
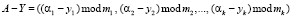 , (2)
, (2)
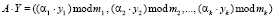 , (3)
, (3)
где 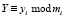 ; i = 1,2,…, k.
; i = 1,2,…, k.
Для получения правильного ответа в МК необходимо, чтобы результаты операций не выходили за пределы рабочего диапазона, определяемого
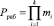 . (4)
. (4)
Анализ выражений (1)–(3) показывает, что операции сложения, вычитания и умножения можно свести к соответствующим операциям по модулю mi, что позволяет повысить скорость вычислений.
Для построения имитостойкой ЗОСРС целесообразно использовать протоколы аутентификации, которые базируются на доказательстве с нулевым разглашением знаний и обладают высокой криптостойкостью. В работе [5] показан протокол аутентификации Фиата – Шамира, для реализации которого требуется t раундов проверки. При этом в каждом раунде выполняется трехшаговый алгоритм интерактивного обмена информацией для проверки претендента несколько раундов. Причем при увеличении числа раундов растет криптостойкость протокола. Аналогичным недостатком обладает протокол аутентификации Гиллоу – Куискуотера [6], также базирующийся на ДНРЗ. Данный протокол использует меньшее количество раундов информационного обмена, чем протокол Фиата – Шамира. Однако для достижения заданной вероятности доказательств корректности представленного идентификатора требуется использование многораундовой процедуры аутентификации.
Устранить данный может протокол аутентификации Шнорра, алгоритм работы которого приведен в [7]. Рассмотрим реализацию данного протокола в модулярном коде. Выбираем в качестве оснований простые числа m1 , m2 , …, mk, для которых ищем простое число qi, – делитель mi. Затем определяется число gi, которое удовлетворяет условию
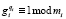 . (5)
. (5)
Секретным ключом выбирают число X = (x1, x2,…, xk), которое удовлетворяет условию
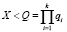 . (6)
. (6)
Открытым ключом является число Y = (у1, у2,…, уk), где справедливо
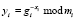 . (7)
. (7)
Протокол аутентификации выполняется следующим образом.
1. Претендент А выбирает случайное число S = (s1, s2,…, sk), которое удовлетворяет условию S < Q. Затем осуществляется вычисление числа R = (r1, r2,…, rk), согласно
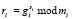 . (8)
. (8)
Вычисленное значение передается проверяющему абоненту В.
2. Абонент В выбирает случайное число 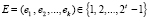 , где t – некоторый параметр. Данное число посылается абоненту А.
, где t – некоторый параметр. Данное число посылается абоненту А.
3. Абонент А, получив число Е, вычисляет число D = (d1, d2,…, dk), согласно равенству
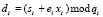 . (9)
. (9)
Вычисленное значение D = (d1, d2,…, dk), посылается абоненту В.
4. Абонент В, получив ответ D = (d1, d2,…, dk), проверяет правильность ответа
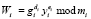 . (10)
. (10)
Если вычисленное значение W = (w1, w2,…, wk) совпадает с числом R = (r1, r2,…, rk), то претендент А – «свой». В противном случае абонент А является «чужим».
Для проведения сравнительного анализа воспользуемся разработанным протоколом аутентификации. В основу данного протокола был положен одномодульный протокол, позволяющий определить статус претендента [8]. Осуществим его реализацию с помощью модулярного кода.
В данном протоколе применяют представленные в МК: секретный ключ 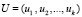 , сеансовый ключ
, сеансовый ключ 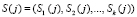 , параметр
, параметр 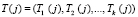 , используемый для уравнения «повторного применения сеансового ключа», где
, используемый для уравнения «повторного применения сеансового ключа», где 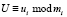 ;
; 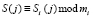 ;
; 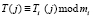 ; i = 1,2,…, k.
; i = 1,2,…, k.
На предварительном этапе аутентификации выполняются следующие вычисления:
1. Претендент А вычисляет истинный статус спутника, представленный в МК
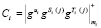 , (11)
, (11)
где g – порождающий мультипликативную группу по модулю mi; i = 1,2,…, k.
2. Претендент А проводит операцию зашумления секретных параметров протокола
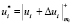 ;
;
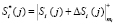 ;
;
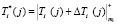 , (12)
, (12)
где 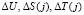 – случайные значения;
– случайные значения; 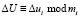 ;
; 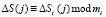 ;
; 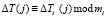 ; i = 1,2,…, k.
; i = 1,2,…, k.
3. Претендент А вычисляет зашумленный статус спутника, используя МК
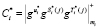 . (13)
. (13)
Алгоритм аутентификации состоит из следующих этапов.
1. Запросчик В передает претенденту А случайное число d = (d1, d2,…, dk).
2. Претендент А, получив d = (d1, d2,…, dk), вычисляет ответы, согласно
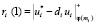 ;
;
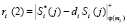 ;
;
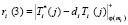 . (14)
. (14)
Претендент А передает запросчику В следующие данные
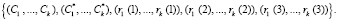
3. Запросчик В осуществляет проверку полученных ответов на вопрос d = (d1, d2,…,dk)
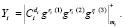 (15)
(15)
Претендент А имеет статус «свой», если выполняется равенство
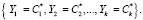 (16)
(16)
Результаты исследования и их обсуждение
Рассмотрим выполнение протокола аутентификации Шнорра в модулярном коде. Выбираем основания модулярного кода МК m1 = 11, m2 = 23, m3 = 29. Рабочий диапазон системы равен Рраб = 7337. Определим делители оснований МК q1 = 5, q2 = 11, m3 = 7, которые имеют Q = 385. Воспользуемся условием (5) и выберем g1 = 3, g1 = 2, g3 = 7. Пусть секретный ключ абонента А равен X = (3, 5, 5). Тогда первая часть открытого ключа, представленного в модулярном коде, будет равна
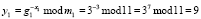 ;
;
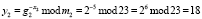 ;
;
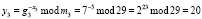 .
.
В этом случае открытый ключ имеет вид (yi, pi, gi) = ((9, 18, 20)(11, 23, 29)(3, 2, 7)).
1. Претендент А выбирает числа S = (2, 7, 3) и вычисляет число R = (r1, r2, r3), согласно
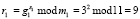 ;
;
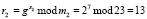 ;
;
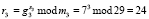 .
.
Вычисленное значение R = (9, 13, 24) передается запросчику В.
2. Запросчик В выбирает число Е = (4, 8, 4), которое передается претенденту А.
3. Претендент А вычисляет ответ на поставленный вопрос е, используя равенство (9)
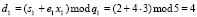 ;
;
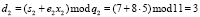 ;
;
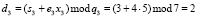 .
.
Вычисленное значение D = (4, 3, 2) посылается абоненту В.
4. Абонент В проверяет правильность ответа согласно (10)
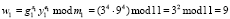 ;
;
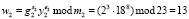 ;
;
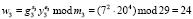 .
.
Так как справедливо, что W = (9, 13, 24) = R, то статус претендента А – «свой».
Рассмотрим выполнение разработанного протокола аутентификации в модулярном коде. Пусть заданы основания m1 = 13, m2 = 19, m3 = 29, для которых имеется g = 2. Рабочий диапазон будет равен Рраб = 7136. В качестве секретного ключа выбираем U = 24 = (11, 5, 24), в качестве сеансового ключа S(j) = 16 = (3, 16, 16), а параметр T(j) = 25 = (12, 6, 25). Воспользуемся выражением (11) и получим истинный статус космического аппарата
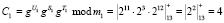 ;
;
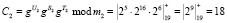 ;
;
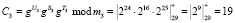 .
.
Истинный статус в коде С = (4, 18, 19) записывается в память спутника.
Выбираем величину «зашумление» равное 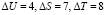 . Тогда получаем следующие зашумленные значения U* = (15, 7, 16), S*(j) = (12, 4, 13) и Т*(j) = (3, 24, 4). Воспользуемся выражение (12) и получим значение зашумленного статуса спутника
. Тогда получаем следующие зашумленные значения U* = (15, 7, 16), S*(j) = (12, 4, 13) и Т*(j) = (3, 24, 4). Воспользуемся выражение (12) и получим значение зашумленного статуса спутника
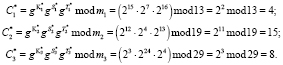
Вычисленное значение зашумленного статуса С* = (4, 15, 8) записывается в память.
Рассмотрим процесс аутентификации спутника. Запросчик, увидев космический аппарат, передает случайное число d = (8, 5, 4). Найдем ответы на вопрос d1 = 8. Получаем
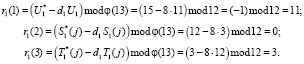
Найдем ответы на вопрос d2 = 5. Получаем следующие ответы:
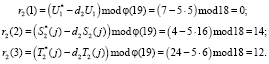
Найдем ответы на вопрос d3 = 4. Получаем следующие ответы:
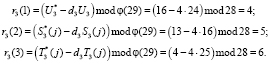
Истинный и зашумленный статусы, а также ответы на случайное число d пересылаются в запросчик. Запросчик проводит проверку статуса космического аппарата
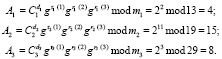
Так как значения 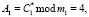
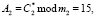
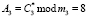 , то запросчик определяет, что космический аппарат «свой», и между спутником и объектом управления начинается обмен данными.
, то запросчик определяет, что космический аппарат «свой», и между спутником и объектом управления начинается обмен данными.
Проведенные исследования показали, что доказывают эффективность использования модулярного кода в рассмотренных протоколах аутентификации, базирующихся на доказательстве с нулевым разглашением данных. Известно, что скорость выполнения мультипликативных операций по модулю пропорциональна разрядности операндов. В рассмотренных примерах использование изоморфизма, порожденного китайской теоремой об остатках, позволило перейти от вычислений с 17 разрядными числами к вычислениям с 5 разрядными операндами. Таким образом, использование модулярного кода позволило повысить скорость проводимых вычислений более чем в 3 раза по сравнению с одномодульной реализацией протокола. Кроме того, полученные результаты наглядно свидетельствуют о том, что разработанный протокол определения статуса спутника, реализованный в модулярном коде, требует в 1,33 раза меньше временных затрат на аутентификацию по сравнению с протоколом Шнорра. Это связано с тем, что разработанный протокол аутентификации содержит меньшее число этапов, необходимых на выявление статуса спутника. Таким образом, разработанный протокол аутентификации, реализованный в модулярном коде, является наиболее перспективным для использования в системах опознавания «свой – чужой».
Заключение
В статье представлен разработанный протокол аутентификации, базирующийся на доказательстве с нулевым разглашением знаний, который реализуется с помощью модулярных кодов. Проведен сравнительный анализ разработанного протокола аутентификации с протоколом Шнорра, при использовании многомодульной реализации. Полученные результаты показали, что разработанный протокол определения статуса спутника, реализованный в модулярном коде, требует в 1,33 раза меньше временных затрат на аутентификации по сравнению с протоколом Шнорра. Полученные результаты свидетельствуют о целесообразности использования разработанного протокола аутентификации, реализованного в модулярном коде, в запросно-ответной системе распознавания спутника.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 17-37-50017.



