Для эффективного решения задач в различных прикладных областях в настоящее время все чаще применяются системы искусственного интеллекта. Задавать всевозможные отношения и причинно-следственные связи между объектами лучше всего с использованием исчисления предикатов первого порядка. В подавляющем большинстве современных интеллектуальных систем для моделирования рассуждений применяется аппарат логического вывода [1, 2] – дедуктивного, индуктивного, абдуктивного, нечеткого методов рассуждений на основе аналогий и прецедентов [3]. Однако нередко в ходе моделирования сложного, многоступенчатого рассуждения требуется определить следствия, которые могут быть выведены из новых фактов, отражающих обстоятельства изменившейся внешней (окружающей) среды при заданном наборе исходных посылок [4]. Для решения поставленной задачи используется специализированный вид дедуктивного вывода – параллельный вывод логических следствий [5].
Формальная постановка задачи логического вывода следствий представлена в работе [6]. Дополнительный интерес может представлять схема, полученная в ходе вывода, которая отражает информацию обо всех возможных траекториях изменения состояния исследуемой системы в прошлом, настоящем и будущем, поэтому в ходе вывода формируется описание O схемы логического вывода в виде семейства множеств O = {f1,f2,…,fh,…,fH-1}∪{s+}, где fh – множество литералов, полученных при формировании описания схемы на h-м шаге вывода, s+ – множество конечных следствий, из которых не могут быть выведены новые следствия (s+⊆MS).
Для осуществления логического вывода с формированием описания схемы используется специальная операция обобщенного деления дизъюнктов.
Применение метода вывода следствий с построением схемы рассмотрим на примере о родственных связях, представленном в работе [7]. Следующие предложения являются исходными данными.
1. Персона (Per) мужского пола, являющаяся родителем (P), называется отцом (F).
2. Отец одного из родителей является дедушкой (GF).
3. Две различные (N) персоны с общим родителем находятся в отношении родных братьев или сестер (S).
4. Родная сестра родителя является тетей (A).
Имеются следующие факты: Виктор (с) – отец Ольги (d), Антонина (b) – персона женского пола (f). Новые факты: Виктор – сын Семена (a), Виктор и Антонина – это не один и тот же человек.
Формальная постановка задачи выглядит следующим образом.
1) F(x,y)[1,+] ∨ Per(x,m)[+,1] ∨ P(x,y)[+,1];
2) GF(x,y)[2,+] ∨ F(x,z)[+,2] ∨ P(z,y)[+,2];
3) S(x,y)[3,+] ∨ P(z,x)[+,3] ∨ P(z,y)[+,3] ∨ N(x,y)[+,3];
4) A(x,y)[4,+] ∨ Per(x,f)[+,4] ∨ P(z,y)[+,4] ∨ S(x,z)[+,4];
5) P(a,b)[5,+];
6) P(c,d)[6,+];
7) Per(a,m)[7,+];
8) Per(b,f)[8,+];
9) Новые факты: P(a,c)[9,+], N(b,c)[9,+].
Логический вывод будет состоять из следующих шагов [6].
1. Определение начальных значений: Определение начальных значений: h = 1, M = {D1, D2, D3, D4, D5, D6} (MF = {D5,D6}), mF = {P(a,c)[9,+], N(b,c)[9,+]}. Формирование выводимого дизъюнкта R1 = P(a,c)[9,+] ∨N(b,c)[9,+], состоящего из литералов, образующих множество mF. Определение множества следствий e0, совпадающих с фактами MF, имеющимися в исходных посылках: e0 = MF∩mF = ∅, s0 = {e0}, c1 = e0 = ∅ Установка начального значения общего признака продолжения вывода: P0 = 0.
2.1. Выполнение 1-й процедуры вывода. v1 = <M,R1,∅,o1,p1,R2,e1,f1>.
2.1.1. Выполняется полное деление дизъюнктов.
Дизъюнкты D1, D2, D3 и D4 делятся на выводимый дизъюнкт R1.
1. Дизъюнкт D1 с помощью W-процедуры делится на выводимый дизъюнкт R1: D1WR1 = (F(x,y)[1,+] ∨ Per(x,m)[+,1] ∨ P(x,y)[+,1])W(P(a,c)[9,+] ∨ N(b,c)[9,+]). Вычисляется матрица «производных» μ[D1,R1] подготовительного шага полного деления дизъюнктов.
|
F(x,y)[1,+] |
Per(x,m)[+,1] |
P(x,y)[+,1] |
|
|
P(a,c)[9,+] |
1 |
1 |
Δ13 |
|
N(b,c)[9,+] |
1 |
1 |
1 |
В матрице l13 = {a/x,c/y}, D13 = F(a,c)[1,+] ∨ Per(a,m)[+,1] = b1, поэтому принимается q = 0, и определяется множество n = {<b1,d1,g1>} (g1 = {P(a,c)[9,{a/x,c/y}1]}). Возможно продолжение частичного деления дизъюнктов. Остаток-делитель d1* = 0, а d1 = P(a,b)[5,+] ∨ P(c,d)[6,+] ∨ Per(a,m)[7,+] ∨ Per(b,f)[8,+].
Дизъюнкт b1 = F(a,c) ∨  Per(a,m) с помощью w-процедуры делится на выводимый дизъюнкт d1. Вычисляется матрица «производных» μ[b1,d1] первого выполнения основного шага процедуры полного деления дизъюнктов.
Per(a,m) с помощью w-процедуры делится на выводимый дизъюнкт d1. Вычисляется матрица «производных» μ[b1,d1] первого выполнения основного шага процедуры полного деления дизъюнктов.
|
F(a,c)[1,+] |
Per(a,m)[+,1] |
|
|
P(a,b)[5,+] |
1 |
1 |
|
P(c,d)[6,+] |
1 |
1 |
|
Per(a,m)[7,+] |
1 |
Δ32 |
|
Per(b,f)[8,+] |
1 |
1 |
В матрице D32 = F(a,c)[1,+] = b1.1, однако остаток-делитель d1.1 = 0, поэтому принимается q = 1. Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов получено множество следствий S1 = {F(a,c)[{a/x,c/y}1,+]} и семейство множеств литералов описания схемы G1 = {{P(a,c)[9,{a/x,c/y}1], Per(a,m)[7,1]}}, Q1 = 0.
2. Дизъюнкт D2 с помощью W-процедуры делится на выводимый дизъюнкт R1: D2WR1 = (GF(x,y)[2,+] ∨ F(x,z)[+,2] ∨ P(z,y)[+,2])W(P(a,c)[9,+] ∨ N(b,c)[9,+]). Вычисляется матрица «производных» μ[D2,R1] подготовительного шага полного деления дизъюнктов.
|
GF(x,y)[2,+] |
F(x,z)[+,2] |
P(z,y)[+,2] |
|
|
P(a,c)[9,+] |
1 |
1 |
Δ13 |
|
N(b,c)[9,+] |
1 |
1 |
1 |
В матрице l13 = {a/z,c/y}, D13 = GF(x,c)[2,+] ∨ F(x,a)[+,2] = b1, поэтому принимается q = 0, и определяется множество n = {<b1,d1,g1>} (g1 = {P(a,c)[9,{a/z,c/y}2]}). Возможно продолжение частичного деления дизъюнктов. Остаток-делитель d1* = 0, а d1 = P(a,b)[5,+] ∨ P(c,d)[6,+] ∨ Per(a,m)[7,+] ∨ Per(b,f)[8,+].
Дизъюнкт b1 = GF(x,c) ∨  F(x,a) с помощью w-процедуры делится на выводимый дизъюнкт d1. Вычисляется матрица «производных» μ[b1,d1] первого выполнения основного шага процедуры полного деления дизъюнктов.
F(x,a) с помощью w-процедуры делится на выводимый дизъюнкт d1. Вычисляется матрица «производных» μ[b1,d1] первого выполнения основного шага процедуры полного деления дизъюнктов.
|
GF(x,c)[2,+] |
F(x,a)[+,2] |
|
|
P(a,b)[5,+] |
1 |
1 |
|
P(c,d)[6,+] |
1 |
1 |
|
Per(a,m)[7,+] |
1 |
1 |
|
Per(b,f)[8,+] |
1 |
1 |
В матрице все производные равны единице, поэтому принимается q = 1. Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов следствий нет: S2 = ∅, G2 = ∅, Q2 = 1.
3. Дизъюнкт D3 с помощью W-процедуры делится на выводимый дизъюнкт R1: D3WR1 = (S(x,y)[3,+] ∨ P(z,x)[+,3] ∨ P(z,y)[+,3] ∨ N(x,y)[+,3])W(P(a,c)[9,+] W N(b,c)[9,+]). Вычисляется матрица «производных» μ[D3,R1] подготовительного шага полного деления дизъюнктов.
|
S(x,y)[3,+] |
P(z,x)[+,3] |
P(z,y)[+,3] |
N(x,y)[+,3] |
|
|
P(a,c)[9,+] |
1 |
Δ12 |
Δ13 |
1 |
|
N(b,c)[9,+] |
1 |
1 |
1 |
Δ24 |
В матрице l12 = {a/z,c/x}, D12 = S(c,y)[3,+] ∨ P(a,y)[+,3] ∨ N(c,y)[+,3] = b1, l13 = {a/z,c/y}, D13 = S(x,c)[3,+] ∨ P(a,x)[+,3] ∨ N(x,c)[+,3] = b2, l24 = {b/x,c/y}, D24 = S(b,c)[3,+] ∨ P(z,b)[+,3] ∨ P(z,c)[+,3] = b3, поэтому принимается q = 0, и определяется множество n = {<b1,d1,g1>, <b2,d2,g2>, <b3,d3,g3>} (g1 = {P(a,c)[9,{a/z,c/x}3]}, g2 = {P(a,c)[9,{a/z,c/y}3]}, g3 = {N(b,c)[9,{b/x,c/y}3]}). Возможно продолжение частичного деления дизъюнктов, d1 = d2 = P(a,b)[5,+] ∨ P(c,d)[6,+] ∨ Per(a,m)[7,+] ∨ Per(b,f)[8,+] ∨ P(a,c)[9,+] ∨ N(b,c)[9,+], d3 = P(a,b)[5,+] ∨ P(c,d)[6,+] ∨ Per(a,m)[7,+] ∨ Per(b,f)[8,+] ∨ P(a,c)[9,+].
Вычисляется матрица «производных» μ[b1,d1] первого выполнения основного шага процедуры полного деления дизъюнктов.
|
S(c,y)[3,+] |
P(a,y)[+,3] |
N(c,y)[+,3] |
|
|
P(a,b)[5,+] |
1 |
Δ12 |
1 |
|
P(c,d)[6,+] |
1 |
1 |
1 |
|
Per(a,m)[7,+] |
1 |
1 |
1 |
|
Per(b,f)[8,+] |
1 |
1 |
1 |
|
P(a,c)[9,+] |
1 |
Δ52 |
1 |
|
N(b,c)[9,+] |
1 |
1 |
1 |
В матрице l12 = {c/y}, D12 = S(c,c)[3,+] ∨ N(c,c)[+,3], l52 = {b/y}, D52 = S(c,b)[3,+] ∨ N(c,b), q = 1. Дальнейшее частичное деление дизъюнктов невозможно.
Вычисляется матрица «производных» μ[b2,d2] первого выполнения основного шага процедуры полного деления дизъюнктов.
|
S(x,c)[3,+] |
P(a,x)[+,3] |
N(x,c)[+,3] |
|
|
P(a,b)[5,+] |
1 |
Δ12 |
1 |
|
P(c,d)[6,+] |
1 |
1 |
1 |
|
Per(a,m)[7,+] |
1 |
1 |
1 |
|
Per(b,f)[8,+] |
1 |
1 |
1 |
|
P(a,c)[9,+] |
1 |
Δ52 |
1 |
|
N(b,c)[9,+] |
1 |
1 |
Δ63 |
В матрице l12 = {b/x}, D12 = S(b,c)[3,+] ∨ N(b,c)[+,3] = b2.1, l52 = {c/x}, D52 = S(c,c)[3,+] ∨ N(c,c)[+,3] = b2.2, l63 = {b/x}, D63 = S(b,c)[3,+] ∨ P(a,b)[+,3] = b2.3, поэтому принимается q = 0, и определяется множество n = {<b2.1,d2.1,g2.1>, <b2.2,d2.2,g2.2>, <b2.3,d2.3,g2.3>} (g2.1 = {P(a,c)[9,{a/z,c/y}3], P(a,b)[5,{b/x}3]}, g2.2 = {P(a,c)[9,{a/z,c/y}3], P(a,c)[9,{c/x}3]}, g2.3 = {P(a,c)[9,{a/z,c/y}3], N(b,c)[9,{b/x}3]}). Возможно продолжение частичного деления дизъюнктов, d2.1 = N(b,c)[9,+], d2.2 = N(b,c)[9,+], d2.3 = P(a,b)[5,+] ∨ P(a,c)[9,+].
Вычисляется матрица «производных» μ[b2.1,d2.1] второго выполнения основного шага процедуры полного деления дизъюнктов.
|
S(b,c)[3,+] |
N(b,c)[+,3] |
|
|
N(b,c)[9,+] |
1 |
Δ12 |
В матрице D12 = S(b,c)[3,+] = b2.1.1, однако остаток-делитель d2.1.1 = 0, поэтому принимается q = 1. Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов получено множество следствий S3 и семейство множеств литералов описания схемы G3, Q3 = 0.
Вычисляется матрица «производных» μ[b2.2,d2.2] второго выполнения основного шага процедуры полного деления дизъюнктов.
|
S(c,c)[3,+] |
N(c,c)[+,3] |
|
|
N(b,c)[9,+] |
1 |
1 |
В матрице все производные равны единице, поэтому принимается q = 1.
Вычисляется матрица «производных» μ[b2.3,d2.3] второго выполнения основного шага процедуры полного деления дизъюнктов.
|
S(b,c)[3,+] |
P(a,b)[+,3] |
|
|
P(a,b)[5,+] |
1 |
Δ12 |
|
P(a,c)[9,+] |
1 |
1 |
В матрице D12 = S(b,c)[3,+] = b2.3.1, однако остаток-делитель d2.2.1 = 0, поэтому принимается q = 1. Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов получено множество следствий S3 и семейство множеств литералов описания схемы G3, Q3 = 0.
Вычисляется матрица «производных» μ[b3,d3] первого выполнения основного шага процедуры полного деления дизъюнктов.
|
S(b,c)[3,+] |
P(z,b)[+,3] |
P(z,c)[+,3] |
|
|
P(a,b)[5,+] |
1 |
Δ12 |
1 |
|
P(c,d)[6,+] |
1 |
1 |
1 |
|
Per(a,m)[7,+] |
1 |
1 |
1 |
|
Per(b,f)[8,+] |
1 |
1 |
1 |
|
P(a,c)[9,+] |
1 |
1 |
D53 |
В матрице l12 = {a/z}, D12 = S(b,c)[3,+] ∨ P(a,c)[+,3], l53 = {a/z}, D53 = S(b,c)[3,+] ∨ P(a,b)[+,3], поэтому принимается q = 0, и определяется множество n = {<b3.1,d3.1,g3.1>, <b3.2,d3.2, g3.2>} (g3.1 = {N(b,c)[9,{b/x,c/y}3], P(a,b)[5,{a/z}3]}, g3.2 = {N(b,c)[9,{b/x,c/y}3], P(a,c)[9,{a/z}3]}). Возможно продолжение частичного деления дизъюнктов, d3.1 = P(a,c)[9,+], d3.2 = P(a,b)[5,+].
Вычисляется матрица «производных» μ[b3.1,d3.1] второго выполнения основного шага процедуры полного деления дизъюнктов.
|
S(b,c)[3,+] |
P(a,c)[+,3] |
|
|
P(a,c)[9,+] |
1 |
Δ12 |
В матрице D12 = S(b,c)[3,+] = b3.1.1, однако остаток-делитель d3.1.1 = 0, поэтому принимается q = 1. Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов получено множество следствий S3 и семейство множеств литералов описания схемы G3, Q3 = 0.
Вычисляется матрица «производных» Δ[b3.2,d3.2] второго выполнения основного шага процедуры полного деления дизъюнктов.
|
S(b,c)[3,+] |
P(a,b)[+,3] |
|
|
P(a,b)[5,+] |
1 |
Δ12 |
В матрице D12 = S(b,c)[3,+] = b3.2.1, однако остаток-делитель d3.2.1 = 0, поэтому принимается q = 1. Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов получено множество следствий S3 = {S(b,c)[{a/z,b/x,c/y}3,+]} и семейство множеств литералов описания схемы G3 = {{N(b,c)[9,{b/x,c/y}3], P(a,c)[9,{a/z}3], P(a,b)[5,3]}}, Q3 = 0.
4. Дизъюнкт D4 с помощью W-процедуры делится на выводимый дизъюнкт R1: D4WR1 = (A(x,y)[4,+] ∨ Per(x,f)[+,4] ∨ P(z,y)[+,4] ∨ S(x,z)[+,4])W(P(a,c)[9,+] ∨ N(b,c)[9,+]). Вычисляется матрица «производных» μ[D4,R1] подготовительного шага полного деления дизъюнктов.
|
A(x,y)[4,+] |
Per(x,f)[+,4] |
P(z,y)[+,4] |
S(x,z)[+,4] |
|
|
P(a,c)[9,+] |
1 |
1 |
Δ13 |
1 |
|
N(b,c)[9,+] |
1 |
1 |
1 |
1 |
В матрице l13 = {a/z,c/y}, D13 = A(x,c)[4,+] ∨ Per(x,f)[+,4] ∨ S(x,a)[+,4] = b1, поэтому принимается q = 0, и определяется множество n = {<b1,d1,g1>}. Возможно продолжение частичного деления дизъюнктов. Остаток-делитель d1* = 0, а d1 = P(a,b)[5,+] ∨ P(c,d)[6,+] ∨ Per(a,m)[7,+] ∨ Per(b,f)[8,+].
Вычисляется матрица «производных» μ[b1,d1] первого выполнения основного шага процедуры полного деления дизъюнктов.
|
A(x,c)[4,+] |
Per(x,f)[+,4] |
S(x,a)[+,4] |
|
|
P(a,b)[5,+] |
1 |
1 |
1 |
|
P(c,d)[6,+] |
1 |
1 |
1 |
|
Per(a,m)[7,+] |
1 |
1 |
1 |
|
Per(b,f)[8,+] |
1 |
Δ42 |
1 |
В матрице l42 = {b/x}, D42 = A(b,c)[4,+] ∨ S(b,a)[+,4] = b1.1, однако остаток-делитель d1.1 = 0, поэтому принимается q = 1.
Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов следствий нет: S4 = ∅, Q4 = 1.
Анализируются признаки решений Q1, Q2, Q3, Q4 выполненных W-процедур. Поскольку Q1 = 0, Q3 = 0, то принимается p1 = 0 и выполняется следующее действие.
2.1.2. Формируется множество следствий и множество литералов описания схемы для выводимого дизъюнкта. Множество e1 образуется путем объединения множеств следствий, полученных при выполнении W-процедур: e1 = S1∪S3 = {F(a,c)[{a/x,c/y}1,+], S(b,c)[{a/z,b/x,c/y}3,+]}. Множество f1 образуется путем включения в него литералов из элементов множеств G1 и G3, соответствующих элементам множества e1, f1 = {P(a,c)[9,{a/x,c/y}1], Per(a,m)[7,1], N(b,c)[9,{b/x, c/y}3], P(a,c)[9,{a/z}3], P(a,b)[5,3]}.
2.1.3. Формируется новый выводимый дизъюнкт. Выводимый дизъюнкт R2 представляет собой дизъюнкцию литералов множества следствий e1: R2 = F(a,c)[{a/x,c/y}1,+] ∨ S(b,c)[{a/z,b/x,c/y}3,+].
2.1.4. Формируется новое множество следствий: С1 = c1∪e1 = {F(a,c)[{a/x,c/y}1,+], S(b,c)[{a/z,b/x,c/y}3,+]}.
2.1.5. Фиксируются результаты выполнения процедуры. Поскольку p1 = 0, то вывод может быть продолжен для дизъюнкта R2 = F(a,c)[{a/x,c/y}1,+] ∨ S(b,c)[{a/z,b/x,c/y}3,+].
Формирование семейства следствий и проверка признаков. Производится формирование семейства множеств следствий s1 = s0∪{e1} = {{F(a,c)[{a/x,c/y}1,+], S(b,c)[{a/z,b/x,c/y}3,+]}} и семейства множеств литералов описания схемы вывода O = O∪{f1} = {{P(a,c)[9,{a/x,c/y}1], Per(a,m)[7,1], N(b,c)[9,{b/x, c/y}3], P(a,c)[9,{a/z}3], P(a,b)[5,3]}}. Формирование общего признака продолжения вывода P1 = P0∪p1 = 0. Поскольку P1 = 0, то принимается h = 2, с2 = С1 и производится переход к п. 2.2
2.2. Выполнение 2-й процедуры вывода. v2 = <M,R2,mF,o2,p2,R3,e2,f2>.
2.2.1. Выполняется полное деление дизъюнктов.
Дизъюнкты D2 и D4 делятся на выводимый дизъюнкт R2.
1. Дизъюнкт D2 с помощью W-процедуры делится на выводимый дизъюнкт R2: D3WR2 = (GF(x,y)[2,+] ∨ F(x,z)[+,2] ∨ P(z,y)[+,2])W(F(a,c)[{a/x,c/y}1,+] ∨S(b,c)[{a/z,b/x,c/y}3,+]). Вычисляется матрица «производных» μ[D2,R2] подготовительного шага полного деления дизъюнктов.
|
GF(x,y)[2,+] |
F(x,z)[+,2] |
P(z,y)[+,2] |
|
|
F(a,c)[{a/x,c/y}1,+] |
1 |
Δ12 |
1 |
|
S(b,c)[{a/z,b/x,c/y}3,+] |
1 |
1 |
1 |
В матрице l12 = {a/x,c/z}, D12 = GF(a,y)[2,+] ∨ P(c,y)[+,2] = b1, поэтому принимается q = 0, и определяется множество n = {<b1,d1,g1>} (g1 = {F(a,c)[{a/x,c/y}1,{a/x,c/z}2]}). Возможно продолжение частичного деления дизъюнктов. Остаток-делитель d1* = 0, а d1 = P(a,b)[5,+] ∨ P(c,d)[6,+] ∨ Per(a,m)[7,+] ∨ Per(b,f)[8,+] ∨ P(a,c)[9,+] ∨ N(b,c)[9,+].
Вычисляется матрица «производных» μ[b1,d1] первого выполнения основного шага процедуры полного деления дизъюнктов.
|
GF(a,y)[2,+] |
P(c,y)[+,2] |
|
|
P(a,b)[5,+] |
1 |
1 |
|
P(c,d)[6,+] |
1 |
Δ22 |
|
Per(a,m)[7,+] |
1 |
1 |
|
Per(b,f)[8,+] |
1 |
1 |
|
P(a,c)[9,+] |
1 |
1 |
|
N(b,c)[9,+] |
1 |
1 |
В матрице l22 = {d/y}, D22 = GF(a,d)[2,+] = b1.1, однако остаток-делитель d1.1 = 0, поэтому принимается q = 1. Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов получено множество следствий S2 = {GF(a,d)[{a/x,c/z,d/y}2,+]} и семейство множеств литералов описания схемы G3 = {{F(a,c)[{a/x,c/y}1,{a/x,c/z}2], P(c,d)[6,{d/y}2]}}, Q3 = 0.
2. Дизъюнкт D4 с помощью W-процедуры делится на выводимый дизъюнкт R2: D4WR2 = (A(x,y)[4,+] ∨ Per(x,f)[+,4] ∨ P(z,y)[+,4] ∨ S(x,z)[+,4])W(F(a,c)[{a/x,c/y}1,+] ∨ S(b,c)[{a/z,b/x,c/y}3,+]).Вычисляется матрица «производных» μ[D4,R2] подготовительного шага полного деления дизъюнктов.
|
A(x,y)[4,+] |
Per(x,f)[+,4] |
P(z,y)[+,4] |
S(x,z)[+,4] |
|
|
F(a,c)[{a/x,c/y}1,+] |
1 |
1 |
1 |
1 |
|
S(b,c)[{a/z,b/x,c/y}3,+] |
1 |
1 |
1 |
Δ24 |
В матрице l24 = {b/x,c/z}, D42 = A(b,y)[4,+] ∨ Per(b,f)[+,4] ∨ P(c,y)[+,4] = b1, поэтому принимается q = 0, и определяется множество n = {<b1,d1,g1>} (g1 = {S(b,c)[{a/z,b/x,c/y}3,{b/x,c/z}4]}). Возможно продолжение частичного деления дизъюнктов. Остаток-делитель d1* = 0, а d1 = P(a,b)[5,+] ∨ P(c,d)[6,+] ∨ Per(a,m)[7,+] ∨ Per(b,f)[8,+] ∨ P(a,c)[9,+] ∨ N(b,c)[9,+].
Вычисляется матрица «производных» μ[b1,d1] первого выполнения основного шага процедуры полного деления дизъюнктов.
|
A(b,y)[4,+] |
Per(b,f)[+,4] |
P(c,y)[+,4] |
|
|
P(a,b)[5,+] |
1 |
1 |
1 |
|
P(c,d)[6,+] |
1 |
1 |
Δ23 |
|
Per(a,m)[7,+] |
1 |
1 |
1 |
|
Per(b,f)[8,+] |
1 |
Δ42 |
1 |
|
P(a,c)[9,+] |
1 |
1 |
1 |
|
N(b,c)[9,+] |
1 |
1 |
1 |
В матрице l23 = {d/y}, D23 = A(b,d)[4,+] ∨ Per(b,f)[+,4] = b1.1, D42 = A(b,y)[4,+] ∨ Per(b,f)[+,4] = b1.2, поэтому принимается q = 0, и определяется множество n = {<b1.1,d1.1,g1.1>, <b1.2,d1.2,g1.2>} (g1.1 = {S(b,c)[{a/z,b/x,c/y}3,{b/x,c/z}4], P(c,d)[6,{d/y}4]}, g1.2 = {S(b,c)[{a/z,b/x,c/y}3,{b/x,c/z}4], Per(b,f)[8,4]}). Возможно продолжение частичного деления дизъюнктов, d1.1 = Per(b,f)[8,+], d1.2 = P(c,d)[6,+].
Вычисляется матрица «производных» μ[b1.1,d1.1] второго выполнения основного шага процедуры полного деления дизъюнктов.
|
A(b,d)[4,+] |
Per(b,f)[+,4] |
|
|
Per(b,f)[8,+] |
1 |
Δ12 |
В матрице D12 = A(b,d)[4,+] = b1.1.1, однако остаток-делитель d1.1.1 = 0, поэтому принимается q = 1. Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов получено множество следствий S4, и семейство множеств литералов описания схемы G4, Q4 = 0.
Вычисляется матрица «производных» μ[b1.2,d1.2] второго выполнения основного шага процедуры полного деления дизъюнктов.
|
A(b,d)[4,+] |
Per(b,f)[+,4] |
|
|
P(c,d)[6,+] |
1 |
Δ12 |
В матрице l12 = {d/y}, D12 = A(b,d)[4,+] = b1.2.1, однако остаток-делитель d1.2.1 = 0, поэтому принимается q = 1. Дальнейшее частичное деление дизъюнктов невозможно. В процессе полного деления дизъюнктов получено множество следствий S4 = {A(b,d)[{b/x,c/z,d/y}4,+]}, и семейство множеств литералов описания схемы G4 = {{S(b,c)[{a/z,b/x,c/y}3,{b/x,c/z}4], P(c,d)[6,{d/y}4], Per(b,f)[8,4]}}, Q4 = 0.
Анализируются признаки решений Q2 и Q4 выполненных W-процедур. Поскольку Q2 = 0, Q4 = 0, то принимается p2 = 0 и выполняется следующее действие.
2.2.2. Формируется множество следствий и множество литералов описания схемы для выводимого дизъюнкта. Множество e2 образуется путем объединения множеств следствий, полученных при выполнении W-процедур: e2 = S2∪S4 = {GF(a,d)[{a/x,c/z,d/y}2,+], A(b,d)[{b/x,c/z,d/y}4,+]}. Множество f2 образуется путем включения в него литералов из элементов множеств G2 и G4, соответствующих элементам множества e2, f2 = {F(a,c)[{a/x,c/y}1,{a/x,c/z}2], P(c,d)[6,{d/y}2], S(b,c)[{a/z,b/x,c/y}3,{b/x,c/z}4], P(c,d)[6,{d/y}4], Per(b,f)[8,4]}.
2.2.3. Формируется новый выводимый дизъюнкт. Выводимый дизъюнкт R3 представляет собой дизъюнкцию инверсий литералов множества следствий e2: R3 = GF(a,d)[{a/x,c/z,d/y}2,+] ∨ A(b,d)[{b/x, c/z, d/y}4,+].
2.2.4. Формируется новое множество следствий: С2 = c2∪e2 = {F(a,c)[{a/x,c/y}1,+], S(b,c)[{a/z,b/x,c/y}3,+], GF(a,d)[{a/x,c/z,d/y}2,+], A(b,d)[{b/x, c/z, d/y}4,+]}.
2.2.5. Фиксируются результаты выполнения процедуры. Поскольку p2 = 0, то вывод может быть продолжен для дизъюнкта R3 = GF(a,d)[{a/x,c/z,d/y}2,+] ∨ A(b,d)[{b/x, c/z, d/y}4,+].
Формирование семейства следствий и проверка признаков. Производится формирование семейства множеств следствий s2 = s1∨{e2} = {{F(a,c)[{a/x,c/y}1,+], S(b,c)[{a/z,b/x,c/y}3,+]}, {GF(a,d)[{a/x,c/z,d/y}2,+], A(b,d)[{b/x, c/z, d/y}4,+]}} и семейства множеств литералов описания схемы вывода O = O∨{f2} = {{P(a,c)[9,{a/x,c/y}1], Per(a,m)[7,1], N(b,c)[9,{b/x,c/y}3], P(a,c)[9,{a/z}3], P(a,b)[5,3]}, {F(a,c)[{a/x,c/y}1,{a/x,c/z}2], P(c,d)[6,{d/y}2], S(b,c)[{a/z,b/x, c/y}3,{b/x,c/z}4], P(c,d)[6,{d/y}4], Per(b,f)[8,4]}}. Формирование общего признака продолжения вывода P2 = P1∨p2 = 0. Поскольку P2 = 0, то принимается h = 3, с3 = С2 и производится переход к п. 2.3.
2.3. Выполнение 3-й процедуры вывода. v3 = <M,R3,mF,o3,p3,R4,e3,f3>.
Ни одно из правил, содержащихся в базе знаний, не делится на выводимый дизъюнкт.
Принимается e3 = ∅, f3 = ∅, C3 = c3, p3 = 1.
2.3.1. Фиксируются результаты выполнения процедуры. Поскольку p3 = 1, то вывод не может быть продолжен.
3. Формирование семейства следствий и проверка признаков. Производится формирование семейства множеств следствий s3 = s2∪{e3} = {{F(a,c)[{a/x,c/y}1,+], S(b,c)[{a/z,b/x,c/y}3,+]}, {GF(a,d)[{a/x,c/z,d/y}2,+], A(b,d)[{b/x, c/z, d/y}4,+]}} и семейства множеств литералов описания схемы вывода O = O∪{f3} = {{P(a,c)[9,{a/x,c/y}1], Per(a,m)[7,1], N(b,c)[9,{b/x,c/y}3], P(a,c)[9,{a/z}3], P(a,b)[5,3]}, {F(a,c)[{a/x,c/y}1,{a/x,c/z}2], P(c,d)[6,{d/y}2], S(b,c)[{a/z,b/x,c/y}3,{b/x,c/z}4], P(c,d)[6,{d/y}4], Per(b,f)[8,4]}}. Формирование общего признака продолжения вывода P3 = P2∪p3 = 1. Поскольку P3 = 1, то вывод завершается. Полученные следствия содержатся в семействе множеств s3, а общее множество следствий получается путем объединения множеств семейства s3: MS = {F(a,c)[{a/x,c/y}1,+], S(b,c)[{a/z,b/x,c/y}3,+], GF(a,d)[{a/x,c/z,d/y}2,+], A(b,d)[{b/x, c/z, d/y}4,+]}. Конечное описание схемы вывода следствий формируется как O = {{P(a,c)[9,{a/x,c/y}1], Per(a,m)[7,1], N(b,c)[9,{b/x,c/y}3], P(a,c)[9,{a/z}3], P(a,b)[5,3]}, {F(a,c)[{a/x,c/y}1,{a/x,c/z}2], P(c,d)[6,{d/y}2], S(b,c)[{a/z,b/x, c/y}3,{b/x, c/z}4], P(c,d)[6,{d/y}4], Per(b,f)[8,4]}, {GF(a,d)[{a/x, c/z,d/y}2,+], A(b,d)[{b/x, c/z, d/y}4,+]}}.
Графическое представление схемы вывода изображено на рисунке.
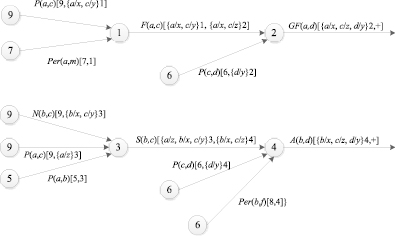
Схема вывода
В ходе решения задачи было показано, что Семен – отец Виктора (F(a,c)), Виктор и Антонина – брат и сестра (S(b,c)), а у Семена имеется внучка Ольга (GF(a,d)), Антонина является тетей Ольги (A(b,d)).
Анализ полученной в ходе осуществления вывода схемы позволяет сделать следующие заключения. Применение предлагаемого метода, в сравнении с классическими методами резолюций Робинсона и обратного вывода Маслова, позволяет сократить число шагов до двух раз с одновременным ростом трудоемкости выполняемых операций. Тем не менее существенный выигрыш в общем времени решения задачи может быть достигнут за счет внутреннего параллелизма, заложенного в базовой операции метода – операции деления дизъюнктов. При этом предварительные результаты экспериментов, проведенных на тестовом наборе сгенерированных машинным способом задач, показали, что в случае ориентации только на AND-параллелизм сокращение временных затрат составляет порядка 21 %. Совмещение AND- и OR-уровней увеличивает выигрыш до 34 %.
Вывод следствий может быть успешно использован как средство сокращения размерности логических задач путем замены статической части системы динамической составляющей. Описание схемы, полученное в ходе выполнения логического вывода, позволит проследить ход решения и может быть использовано при оценке развития ситуации, если предположить, что анализируемая система находится в динамическом состоянии, отраженном на схеме. Подобные задачи особенно часто возникают в таких областях как поддержка принятия решений, прогнозирование [8], мониторинг, диагностика[9], формальная верификация [10] и так далее.



