Получение научных результатов в настоящее время невозможно представить без предварительного моделирования на компьютере, что значительно снижает стоимость любой разработки, так как математическая модель объекта управления является ключевым элементом исследований в авиационной промышленности до натурных или полунатурных испытаний газотурбинного двигателя (ГТД), существует возможность проанализировать и провести предварительные исследования, поэтому целесообразно совершенствовать методы моделирования динамики ГТД.
Процессы, происходящие при работе двигателя и топливной автоматики, имеют сложный нелинейный характер, при этом они соразмеримы по времени, что является актуальным при работе короткоресурсных двигателей для беспилотных летательных аппаратов (БПЛА). Ранее объект управления рассматривался как единое целое, включая в себя агрегат дозирования топлива (АДТ) и сам ГТД, при этом динамическая характеристика (ДХ) для проектирования системы автоматического управления (САУ) представлялась в виде апериодического звена первого порядка [1]. Такое представление объекта управления не позволяет учитывать нелинейные процессы, происходящие как в топливной автоматике, так и в самом двигателе, что существенно снижает качество управления всей системы автоматического управления БПЛА в целом.
Достаточно длительное время для моделирования ГТД используют ДХ двигателя, применяя кусочно-линейный метод аппроксимации нелинейных характеристик и выбирая один режим работы (стабилизацию). К недостаткам такого подхода моделирования ДХ двигателя относится невозможность охвата всех нелинейных кривых, а также трудности в «склейке» полученных полиномов, при этом синтезировались лишь алгоритмы управления режимом стабилизации. Управление режимами разгона, как правило, носило эмпирический характер, программа разгона корректировалась в процессе натурных испытаний.
Для того чтобы управлять всеми режимами работы двигателя в условиях его применения, предлагается использовать матричное представление самой ДХ, которое будет охватывать весь диапазон режимов работы двигателя. В перспективе подобный подход будет использован и для моделирования АДТ, что позволит построить динамику «неизменяемой» части САУ в едином информационном пространстве.
Нейронные сети долгое время рассматриваются как универсальный подход к построению математических моделей систем, они позволяют эффективно находить приближенные решения начально-краевых задач для уравнений в частных производных, учитывать нелинейные эффекты и возмущения коэффициентов [2]. Новизна настоящей работы заключается в использовании двух нейронных сетей при разработке модели ГТД, что позволит учитывать весь диапазон нелинейных кривых ДХ, представленной в виде матриц.
Целью работы является разработка матричного подхода к моделированию ГТД с помощью нейронных сетей, что позволит достаточно точно отразить динамические процессы в ГТД во всем диапазоне режимов работы и условий применения.
Постановка задачи
Рассмотрим ДХ ГТД, представляющую собой зависимость трех параметров: расход топлива  , частота вращения ротора турбокомпрессора
, частота вращения ротора турбокомпрессора 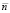 , скорость изменения частоты вращения ротора турбокомпрессора
, скорость изменения частоты вращения ротора турбокомпрессора 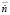 (рис. 1). Все параметры ДХ представлены в приведенных значениях.
(рис. 1). Все параметры ДХ представлены в приведенных значениях.
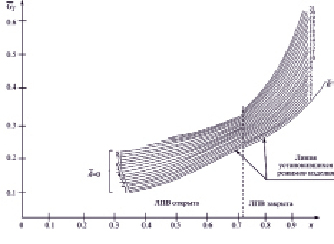
a)
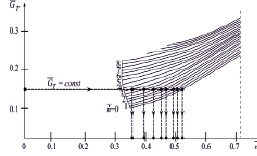
б)
Рис. 1. Динамическая характеристика силовой установки БПЛА, где (а) 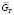 ДХ является графическим отображением статических и динамических свойств ГТД в широком диапазоне режимов работы. Используя подход к проектированию математической модели двигателя на основе матричного представления ДХ [3], необходимо разработать модель ГТД, охватывающую весь диапазон режимов работы и условий применения.
ДХ является графическим отображением статических и динамических свойств ГТД в широком диапазоне режимов работы. Используя подход к проектированию математической модели двигателя на основе матричного представления ДХ [3], необходимо разработать модель ГТД, охватывающую весь диапазон режимов работы и условий применения.
Методы решения
Воспользуемся методом матричного представления ДХ, описанным в работе [3]. Суть метода заключается в фиксации параметров ДХ в виде матриц. В работе используется матрица по расходу топлива 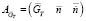 . Для того чтобы провести «склейку» матриц и сгладить переход на границе перепуска ленты, матрица по расходу топлива разбивается на две части:
. Для того чтобы провести «склейку» матриц и сгладить переход на границе перепуска ленты, матрица по расходу топлива разбивается на две части: 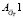 и
и 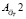 . Матрица
. Матрица 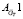 соответствует области ДХ до значения количества оборотов турбокомпрессора
соответствует области ДХ до значения количества оборотов турбокомпрессора 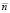 = 0,72, когда срабатывает лента перепуска воздуха, а матрица
= 0,72, когда срабатывает лента перепуска воздуха, а матрица 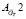 – области ДХ после этого значения.
– области ДХ после этого значения.
Для разработки математической модели двигателя необходимо решить задачу непрерывного по времени перехода с режима на режим ДХ на всем многообразии режимов работы и условий применения.
Модель двигателя в среде имитационного моделирования Simulink представляет собой блок, на вход которого поступают приведенные значения расхода топлива и частоты вращения ротора турбокомпрессора, а на выходе формируется приведенное значение ускорения ротора.
Блок модели ГТД в Simulink с использованием двух нейронных сетей на основе матричного подхода представлен на рис. 2.
alt="den04.wmf" /> – относительное значение расхода топлива, 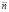 – относительная частота вращения ротора,
– относительная частота вращения ротора, 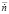 – относительное ускорение ротора; (б) Пример образования матрицы значений по расходу топлива (
– относительное ускорение ротора; (б) Пример образования матрицы значений по расходу топлива (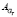 )
)
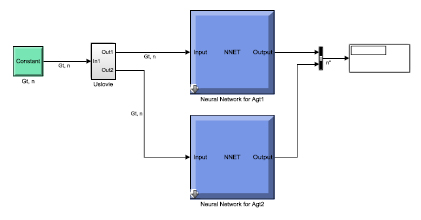
Рис. 2. Блок модели ГТД в Simulink с использованием двух нейронных сетей на основе матричного подхода
Логика работы блока модели ГТД заключается в следующем.
На вход блока модели ГТД поступают два значения параметров: расход топлива и частота вращения ротора турбокомпрессора в приведенных значениях, в среде моделирования Simulink эти параметры представлены в виде блока константы (Constant). Далее сигналы поступают на вход блока условия (Uslovie): если значение частоты вращения ротора турбокомпрессора 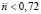 , то входные данные поступают в блок нейронной сети, обученной на основе матрицы по расходу топлива
, то входные данные поступают в блок нейронной сети, обученной на основе матрицы по расходу топлива 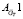 (Neural Network for Agt1), иначе – на вход матрицы
(Neural Network for Agt1), иначе – на вход матрицы 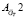 (Neural Network for Agt2). Нейронные сети введены и обучены для поиска входных значений, которые совпадают и не совпадают с матричными, что является объективным, так как при работе ГТД не могут быть получены значения параметров, в точности соответствующие матричным. На выходе формируется значение ускорения ротора турбокомпрессора
(Neural Network for Agt2). Нейронные сети введены и обучены для поиска входных значений, которые совпадают и не совпадают с матричными, что является объективным, так как при работе ГТД не могут быть получены значения параметров, в точности соответствующие матричным. На выходе формируется значение ускорения ротора турбокомпрессора 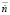 , которое соответствует входным данным, найденным в матрице по расходу топлива.
, которое соответствует входным данным, найденным в матрице по расходу топлива.
Для аппроксимации заданного набора входных-выходных данных можно воспользоваться различными подходами. Чтобы не искать явный вид функциональной зависимости, используем нейронную сеть для ее описания. Нейронные сети являются универсальными аппроксиматорами сложных нелинейных функциональных зависимостей [3].
Для обучения нейронной сети не требуется никакой априорной информации о структуре искомой функциональной зависимости. Нужна лишь обучающая выборка в виде экспериментальных пар «вход-выход».
Обычно для обучения нейронной сети необходимо выполнить предобработку исходных данных, которая заключается в нормализации данных, то есть необходимо привести числовые значения к конкретному диапазону значений, например, от 0 до 1 или от –1 до 1. В данном случае в этом нет необходимости, так как исходные данные уже лежат в этом диапазоне: X меняется от 0,08 до 0,26, Y меняется от 0,35 до 0,69, где X – вектор входных параметров (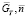 ), а Y – выходной параметр (
), а Y – выходной параметр (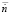 ).
).
Для решения поставленной задачи выберем многослойный персептрон, обучаемый согласно алгоритму обратного распространения ошибки, так как доказана применимость теоремы об универсальной аппроксимации к многослойному персептрону.
Число нейронов во входном и выходном слоях соответствует числу входных и выходных параметров: во входном слое – 4, в выходном – 2.
В структуре сети существует один скрытый слой (рис. 3), так как теорема об универсальной аппроксимации утверждает, что многослойного персептрона с одним скрытым слоем достаточно для построения равномерной аппроксимации с точностью e для любого обучающего множества, представленного набором входов и откликов. Количество нейронов в скрытом слое примем 50 [4]. Как показали представленные далее результаты, такое количество нейронов обеспечивает необходимую точность аппроксимации и низкие затраты на время обучения нейронной сети.
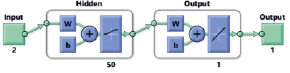
Рис. 3. Структура нейронной сети
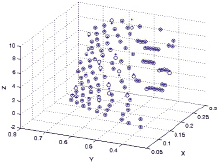
a)
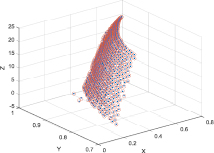
б)
Рис. 4. Результаты аппроксимации: (а) для матрицы по расходу топлива 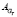 1; (б) для матрицы по расходу топлива
1; (б) для матрицы по расходу топлива 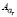 2
2
Во входном слое используем сигмоидальную функцию активации, в выходном – линейную, что обусловлено простотой применения, обучения и статистического анализа [5]. На рис. 4 представлен результат аппроксимации исходных данных нейронной сетью, где «.» показаны экспериментальные данные, «o» – выход нейронной сети. Средняя ошибка аппроксимации составляет 0,018.
Результаты
Разработан блок модели ГТД для имитационного моделирования в среде Simulink с использованием двух нейронных сетей. В таблице представлены результаты работы блока и приведено сравнение с матричными значениями для матрицы по расходу топлива 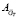 . В таблицу внесены данные расхода топлива и частоты вращения ротора турбокомпрессора, взятые из матрицы, на основе которой была построена нейронная сеть: промежуточные значения расхода топлива и количества оборотов, которые могут быть получены в ходе работы двигателя и могут не совпадать с матричными; приведен диапазон значений ускорения ротора турбокомпрессора, в который должно «попасть» значение ускорения ротора при работе нейронной сети.
. В таблицу внесены данные расхода топлива и частоты вращения ротора турбокомпрессора, взятые из матрицы, на основе которой была построена нейронная сеть: промежуточные значения расхода топлива и количества оборотов, которые могут быть получены в ходе работы двигателя и могут не совпадать с матричными; приведен диапазон значений ускорения ротора турбокомпрессора, в который должно «попасть» значение ускорения ротора при работе нейронной сети.
Результаты работы блока модели ГТД
|
Значения входных параметров, соответствующие матричным |
Сравнение матричного значения ускорения ротора с результатами работы НС |
Значение входных параметров, представленных в произвольном виде |
Сравнение диапазона возможных матричных значений ускорения ротора с результатами работы НС |
||||
|
|
|
|
|
|
|
|
|
|
0,16 |
0,68 |
0,5 |
0,49 |
0,163 |
0,4 |
0,38–0,44 |
3,924 |
|
0,17 |
0,665 |
1,5 |
1,416 |
0,179 |
0,645 |
2,5–3,5 |
2,965 |
|
0,19 |
0,34 |
5,5 |
5,549 |
0,195 |
0,52 |
5–5,5 |
5,44 |
|
0,19 |
0,69 |
2,5 |
1,956 |
0,211 |
0,675 |
4–6 |
4,154 |
|
0,2 |
0,69 |
3,5 |
2,5 |
0,237 |
0,52 |
8–8,5 |
8,378 |
|
0,17 |
0,73 |
0 |
0,0958 |
0,207 |
0,7355 |
5–6 |
6,252 |
|
0,2 |
0,745 |
4 |
4,218 |
0,243 |
0,781 |
7–8 |
6,935 |
|
0,24 |
0,789 |
6 |
5,346 |
0,315 |
0,765 |
20–21 |
20,16 |
|
0,27 |
0,81 |
7 |
7,086 |
0,505 |
0,922 |
16–17 |
16,93 |
|
0,32 |
0,89 |
1 |
0,9506 |
0,557 |
0,913 |
21–22 |
21,93 |
|
0,46 |
0,88 |
20 |
20,18 |
0,593 |
0,954 |
18–19 |
18,08 |
|
0,51 |
0,9 |
21 |
20,69 |
0,616 |
0,9195 |
24–24 |
24,08 |
Из таблицы видно, что нейронная сеть полностью отрабатывает полученные на входе значения, которые удовлетворяют матричным значениям.
Заключение
В настоящей статье разработан блок для имитационного моделирования математической модели ГТД на основе ДХ с помощью матричного подхода и нейронных сетей. Показан блок ГТД в среде моделирования Simulink. Приведены результаты работы данного блока. Полученная модель будет применяться при моделировании САУ ГТД, а также может быть использована для согласования динамики работы АДТ и ГТД.
К достоинствам проведенного исследования моделирования ГТД, реализованного в виде двух нейронных сетей на основе матричного подхода, можно отнести следующее: ДХ воспроизводится во всем диапазоне режимов работы и условий применения в виде модели двигателя: от разгона до выхода на режим стабилизации; в дальнейшем разработанный подход позволит подбирать алгоритм управления режимом разгона с переходом на режим стабилизации; повысить точность управления силовой установкой. Использование двух нейронных сетей позволяет находить значения на всей рабочей области ДХ.




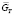
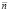
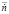 (Матричное значение)
(Матричное значение)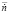 (Полученное при работе блока)
(Полученное при работе блока)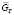
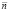
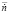 (Матричное значение)
(Матричное значение)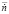 (Полученное при работе блока)
(Полученное при работе блока)