Решение проблемы повышения качества обработки заготовок на станках с ЧПУ определяется режимами обработки, условиями протекания процессов и характером изменения параметров процесса и влияющих величин. Значительным недостатком станков с ЧПУ является то, что они зачастую не гарантируют заданных жестких требований по точности и качеству обработки деталей вследствие недетерминированности процесса и нестационарности условий обработки.
Автоматическое поддержание работоспособности станочного оборудования в условиях минимального вмешательства оператора («безлюдная технология») невозможно без широкого использования встроенных средств, осуществляющих сбор информации о качестве протекания технологического процесса. Помимо сбора информации должна присутствовать и функция принятия решений по ликвидации последствий отказов [1]. Большинство запросов на создание систем управления технологическим процессом возникают в тех случаях, когда станки находятся в эксплуатации и затруднена сложная модернизация.
Динамические процессы в технологических системах существенно влияют на устойчивость процесса резания, качество и точность механической обработки. Технологическую обрабатывающую систему можно представить как совокупность взаимосвязанных открытых нелинейных динамических подсистем с прямыми и обратными связями и иерархическим устройством.
Система резания является основной подсистемой технологической системы. Необходимая устойчивость процесса резания достигается при самоорганизации системы. Однако в процессе резания устойчивое движение упругой системы станок – инструмент – деталь нарушается переходом к хаотическому движению. Число степеней свободы, определяющее вид траектории движения системы в фазовом пространстве, зависит от того, сколько параметров необходимо задать, чтобы полностью охарактеризовать в нем состояние системы.
Рассматривая технологическую систему как совокупность механической подсистемы (станок) с трибосредой (контакт резца с обрабатываемой деталью), можно отметить, что при их взаимодействии формируется новая система (трибосистема) [2]. Для более эффективного использования станков необходим подход к управлению процессом резания, основанный на анализе устойчивости технологической обрабатывающей системы.
Управление процессом на базе корректных математических моделей процесса резания металлов возможно только при наличии набора экспериментальных данных о динамических процессах и установлении законов изменения параметров технологической обрабатывающей системы.
Выбор средств (датчиков) для оперативной диагностики процесса резания определяется в основном двумя факторами: информативностью, адекватной ситуации, возникающей в зоне резания, а также простотой и надежностью встройки в станок. Использование высокочастотных колебаний (в частотном диапазоне выше 100–500 кГц) затруднено тем, что вибрации быстро затухают с увеличением расстояния от источника их возникновения.
Природа вибраций в трибосистеме имеет сложную структуру. Основное преимущество виброакустического сигнала, генерируемого в процессе обработки в диапазоне до 20–30 кГц, заключается в том, что его можно регистрировать в любой точке упругой системы станка.
Динамические явления, возникающие в процессе резания, определяются не только режимами резания, но и состоянием режущего инструмента, размерный износ которого становится источником проблем при определении необходимой коррекции [3].
Экспериментальные исследования влияния параметров лезвийной обработки стальных деталей на устойчивость процесса резания
Для оценки устойчивости процесса резания был проведен ряд экспериментов. Эксперимент проводился с использованием автоматизированного стенда (рис. 1). В ходе эксперимента измерялся виброакустический сигнал и контролировался износ режущего инструмента [4].
Эксперимент проводился в условиях: механическая подсистема – токарно-обрабатывающий центр SuperJobber 500; обрабатываемый материал – сталь 45, 40Х; режущий инструмент – минералокерамический инструмент ВОК60, твердый сплав Т15К6; условие сухого трения (отсутствие смазывающе-охлаждающих жидкостей); скорость обработки – v = 200–400 м/мин; подача s = 20–150 мм/мин; глубина резания t = 0,25 мм. Во время обработки каждой детали фиксировался виброакустический сигнал с помощью трехкоординатного пьезоакселерометра с частотным диапазоном 0–21 кГц.
Наряду с записью виброакустического сигнала для определения устойчивости технологической обрабатывающей системы контролировался износ режущего инструмента по задней поверхности. Было установлено, что на первом этапе процесса резания виброакустический сигнал характеризуется высокими амплитудами трех различных направлений. При дальнейшей обработке частотный спектр вибросигнала изменялся с концентрацией основной мощности в нескольких явно выраженных частотных диапазонах. Уменьшение спектральной функции наблюдалось до износа режущего инструмента h3 = 0,2–0,3 мм по задней грани. При увеличении износа от 0,2–0,3 мм до 0,6–0,7 мм обнаруживается стабильность мощности вибросигнала. Достижение величины износа 0,7 мм соответствует возрастанию мощности вибросигнала в диапазоне частот от 8 кГц до 14 кГц значительнее, чем в других областях спектра.
Уменьшение амплитуды вибрации объясняется увеличением фрикционного демпфирования вследствие увеличения площади контакта между инструментом и заготовкой.
В процессе обработки поверхностей заготовки происходит сглаживание наиболее выступающих неровностей, формируется новая поверхность, а трибологическая система переходит в равновесное состояние. Сформированная шероховатость является оптимальной для данных условий взаимодействия и обеспечивает минимальный износ. Данная стадия изнашивания инструмента является стационарным процессом и характеризуется постоянной величиной основных параметров трения [4].
Математические модели оценки устойчивости процесса резания на основе нечеткой логики и модели Лоренца
В случае невозможности применения простых математических моделей для описания сложных систем и процессов, систем с существенной нелинейностью [5], их описание возможно помощью применения методов нечеткой логики.
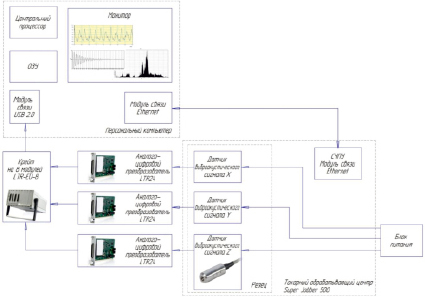
Рис. 1. Структура автоматизированного стенда измерения вибросигнала при чистовой обработке
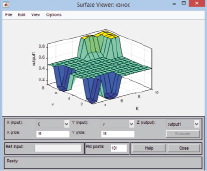
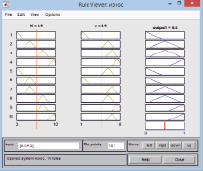
а) б)
Рис. 2. Модель износа инструмента
В рамках нечеткой логики механизм логического вывода в общем случае состоит из следующих этапов [6]:
1. Фазификация.
2. Нечеткий вывод.
3. Нечеткая композиция.
4. Дефазификация.
На рис. 2 показаны поверхность функции модели (а) и задание системы правил функции (б), реализованные с помощью модуля fuzzy logic программного обеспечения Matlab.
2,547 мкм 0,618 мкм 0,600 мкм
а) б) в)
|
S = 0,1 мм/об V = 300 м/мин |
S = 0,1 мм/об V = 350 м/мин |
S = 0,1 мм/об V = 400 м/мин |
г) д) е)
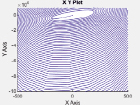
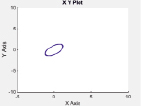
Рис. 3. Фотографии обработанной поверхности (а), профилограммы поверхности (б), параметры шероховатости Ra (в), полигоны распределения частот (г), фазовые портреты технологической системы (д) при различных режимах резания (е)
Для исследования технологической системы процесса резания в программном пакете Simulink Matlab R2014 была построена модель системы Лоренца [7] для технологической системы. Результаты расчетов выводятся на блок графопостроителя фазовой плоскости XY и XZ.
Для оценки параметров исследуемой системы Лоренца использовался уточненный метод Эйлера. Модель системы имеет вид
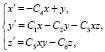
где параметры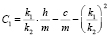 
, 
, 
, 
, 
, 
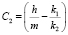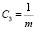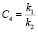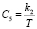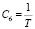, среди которых оценка проводилась для С1, С2, С4, С5 [8].
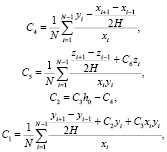
где xi, yi, zi – значения временных рядов на i-ом шаге соответственно, N = 104 – длина временного ряда, H = 0,01 – шаг интегрирования. Значения временных рядов брались из стадии стационарного процесса (износ по задней поверхности hз = 0,3–0,7 мм).
Для оценки устойчивости трибосистемы принципиальное значение имеют два параметра С1 и С2, так как они определяют знак в системе. Коэффициент С1, характеризующий частоту колебаний в системе, можно представить как функцию от с. Поэтому параметр С1 (а точнее с) в системе будет управляющим. По мере движения точки равновесия системы изменяются значения динамической жесткости и диссипации.
Коэффициент суммарной динамической жесткости [8]:
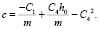
Для различных значений с были построены фазовые портреты, по которым определялась устойчивость системы (рис. 3).
Выводы
Проверка адекватности модели показала, что с точки зрения управляемости процесса особенный интерес для трибосистемы представляет случай, когда параметры системы определяют её положение вблизи бифуркационных преобразований, при этом достаточно малого изменения управляющих параметров для того, чтобы система самопроизвольно перешла в состояние детерминированного поведения, т.е. наблюдается ее спонтанная самоорганизация.
В результате экспериментов было выявлено [8]:
– при с = 0; –11 < с < –17; –24 < c < –27 система находится в состоянии бифуркации и способна самопроизвольно перейти в новое состояние;
– при остальных отрицательных значениях с система относительно устойчива;
– при положительных значениях с система имеет единственную асимптотически устойчивую точку, где она является относительно устойчивой, при обработке как минералокерамическим инструментом ВОК60 так и твердым сплавом Т15К6, но данные режимы обработки не являются оптимальными с точки зрения производительности процесса.