Оригинальные способы решения задач технической механики по определению реакций идеальных связей в плоской системе сходящихся сил рассмотрены в нескольких статьях, опубликованных автором в периодических научных изданиях [1–3]. Важный вывод, вытекающий из представленных рассуждений, заключается в возможности творчески подходить к решению учебных задач. В частности, эффективной формой, способствующей выражению творчества, в учреждении среднего профессионального образования (далее СПО) может быть организация мини-исследования по нахождению реактивных сил по известным факторам активной нагрузки.
Задачи статики традиционно считаются консервативными, поэтому обычно решаются по общепринятым алгоритмам. Усвоение последовательности, способов и приемов действий при расчете реакций в связях указывает на овладение учащимися основами методики решения задач. Однако актуальность развития в настоящее время компетентности и креативных качеств личности побуждает к поиску возможностей решения учебных задач новыми способами, не описанными ранее в методической и учебной литературе, что способствует совершенствованию методики обучения решению статических задач.
Цель исследования
В настоящей статье раскроем положения, направленные на совершенствование методики обучения решению задач статики по определению опорных реакций балок на двух шарнирах и основанные на использовании нового метода, сущность которого заключается в последовательных эквивалентных преобразованиях и уравновешивании внешней нагрузки.
Материалы и методы исследования
В процессе исследовательской работы пересмотрены методические основы обучения решению учебных задач по определению реакций, возникающих под внешней нагрузкой в связях балок на двух опорах, в курсе технической механики в организациях, реализующих ФГОС СПО по техническим и технологическим специальностям. Проанализирована отечественная и зарубежная методическая и учебная литература по технической механике, обобщен педагогический опыт, изучены продукты деятельности обучающихся, использованы экспертная оценка, моделирование, педагогическое наблюдение, качественный и количественный анализ фактического материала, методы математической статистики, а также сравнение и аналогия, формулирование выводов и обобщение. Как результат, предложен новый метод решения исследуемого вида задач статики, который аналитически независим от традиционного способа, а в совокупности с ним позволяет достоверно подтвердить или опровергнуть истинность полученных результатов.
Результаты исследования и их обсуждение
Выберем конкретную задачу, в которой силы приложены к балке вертикально (рис. 1). Именно такой особенностью отличаются задания для обучающихся образовательных организаций СПО, включенные в сборники задач по технической механике. Пример тому учебное пособие В.И. Сеткова [4], откуда и заимствовано задание.
Традиционно решение начинается с замены распределенной нагрузки эквивалентной сосредоточенной силой Q. Так как q = const, то Q = q•c = 15•6 = 90 (кН). Точка приложения Q приходится на середину участка длиной с = 6 (м), а направление Q совпадает с направлением нагрузки q. Затем выбираются вероятные направления реакций RA и RB, реализуется принцип освобождаемости и применяются условия равновесия. Целесообразно при этом опоры балки A и B рассматривать в качестве точек, относительно которых составляются уравнения для моментов. В нашем случае:
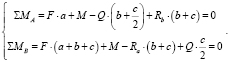
Каждое уравнение содержит по одной неизвестной величине, что позволяет выразить и рассчитать искомые реактивные силы. Из второго равенства находится реакция RA:
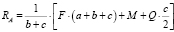
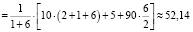 (кН), (1)
(кН), (1)
а из первого равенства – реакция RB:
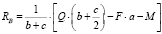
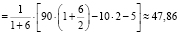 (кН). (2)
(кН). (2)
Знаки вычисленных реактивных сил («+» или «–») указывают на правильность или ошибочность предположений об их вероятных направлениях. У нас знаки положительные (RA > 0 и RB > 0), значит, реакции действительно направлены вверх.
Проверка правильности найденных значений реакций производится составлением и решением уравнения равновесия для вертикальных сил после условно принятого положительного направления, например кверху. Если равенство ΣY = 0 cоблюдается, как в рассматриваемом примере, –F + RA – Q + RB = –10 + 52,14 – 90 + 47,86 = 0, то делается заключение о верном решении задачи.
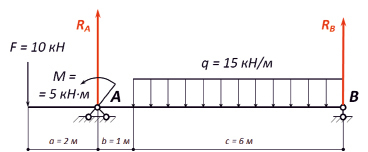
Рис. 1. Исходные данные задачи по определению реакций опор балки с выбранными направлениями реактивных сил RA и RB
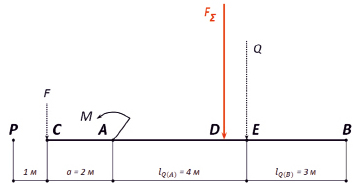
Рис. 2. Преобразования по замене сначала распределенной нагрузки q сосредоточенной силой Q, а затем ее вместе с активной силой F равнодействующей FΣ
Следует обратить внимание, и на это указывает многолетний опыт преподавания технической механики в учреждениях СПО, что именно проверка в традиционной методике обучения решению задач по определению реакций опор балки является релятивной, а поэтому недостаточно надежной для достоверного заключения о правильности нахождения реактивных сил. В вычислениях обучающихся имеют место случаи, когда условие равновесия для вертикальных сил выполняется, а реакции не соответствуют истинным значениям. Или, что происходит нередко, по невнимательности обучающиеся путают значения RA и RB. В сопротивлении материалов, когда расчет опорных реакций является начальным этапом решения задач на изгиб балки, такая ошибка приводит к неправильному определению поперечных сил и изгибающих моментов в сечениях, неверному выбору номера профиля проката или вычислению размеров поперечного сечения балки.
Способ определения реакций в опорах балки, предлагаемый нами, основан на последовательных эквивалентных преобразованиях и уравновешивании внешней нагрузки. Сущность метода заключается в том, что после замены распределенной нагрузки q равнозначной сосредоточенной силой Q находится равнодействующая F∑ внешних сил и точка ее приложения: либо по правилам для параллельных одинаково направленных сил, как в нашем примере,
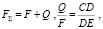
где C, D, E – точки приложения соответственно сил F, F∑, Q (рис. 2); либо по правилам для параллельных противоположно направленных сил.
Если в условии задачи указано более двух распределенных нагрузок и активных сил, то вместо последовательного нахождения равнодействующей каждый раз для двух сил удобнее воспользоваться правилом для моментов, создаваемых этими силами относительно произвольной точки плоскости. Исключение составляют точки A и B. Например, можно выбрать точку P, расположенную на линии балки, слева от точки C на расстоянии 1 м. Тогда длину отрезка CD в нашей задаче можно определить следующей зависимостью:
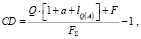
где lQ(A) – расстояние от линии действия силы Q до точки A, 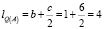 (м).
(м).
Поскольку 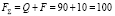 (кН), то
(кН), то 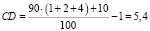 (м).
(м).
Далее силу F∑ необходимо уравновесить возникающими в ответ на ее действие реактивными силовыми составляющими 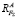 и
и 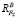 в опорах балки. Направление сил
в опорах балки. Направление сил 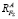 и
и 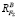 можно установить из условия равновесия моментов относительно точек опор. В нашей задаче сила F∑ относительно точки A создает отрицательный момент, для уравновешивания которого требуется положительный момент, создаваемый ответной реактивной составляющей
можно установить из условия равновесия моментов относительно точек опор. В нашей задаче сила F∑ относительно точки A создает отрицательный момент, для уравновешивания которого требуется положительный момент, создаваемый ответной реактивной составляющей 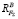 , значит,
, значит, 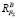 направлена противоположно F∑ (рис. 3):
направлена противоположно F∑ (рис. 3):
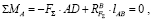
где
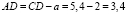 (м),
(м),
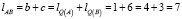 (м),
(м),
поэтому 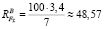 (кН).
(кН).
Относительно точки B сила F∑ создает положительный момент, уравновесить который должен отрицательный момент реактивной составляющей 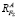 , поэтому
, поэтому 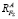 тоже направлена противоположно F∑ (рис. 3):
тоже направлена противоположно F∑ (рис. 3):
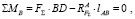
так как 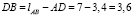 (м), то
(м), то 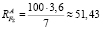 (кН).
(кН).
Проверку полученных направлений ответных реактивных силовых составляющих 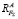 и
и 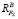 можно выполнить с помощью правил, вытекающих из анализа принципов сложения параллельных сил:
можно выполнить с помощью правил, вытекающих из анализа принципов сложения параллельных сил:
- если равнодействующая F∑ проходит между точкам A и B, как в нашем случае, то силовые составляющие
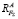 и
и 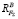 одинаково направлены (рис. 3);
одинаково направлены (рис. 3); - если равнодействующая F∑ находится по одну сторону (правую или левую) от точек A и B, то силовые составляющие
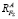 и
и 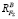 противоположно направлены.
противоположно направлены.
Остается уравновесить внешний момент M эквивалентной парой сил 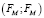 с плечом, равным расстоянию между опорами A и B, то есть lAB. Если в условии задачи предлагается несколько моментов, то находится главный момент M∑ суммированием с учетом направления каждого из них, то есть
с плечом, равным расстоянию между опорами A и B, то есть lAB. Если в условии задачи предлагается несколько моментов, то находится главный момент M∑ суммированием с учетом направления каждого из них, то есть 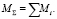 В рассматриваемой задаче внешний момент один (рис. 4), поэтому
В рассматриваемой задаче внешний момент один (рис. 4), поэтому 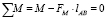 , откуда
, откуда 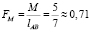 (кН).
(кН).
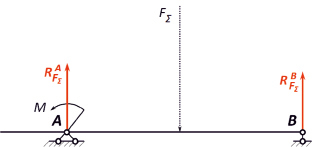
Рис. 3. Уравновешивание равнодействующей F∑ составляющими 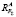 и
и 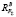
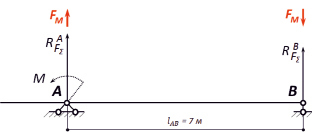
Рис. 4. Уравновешивание момента M в парой сил FM с плечом lAB
Моментные составляющие FM линиями действия совпадают с силовыми составляющими 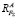 и
и 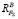 и образуют с ними коллинеарные векторы. Следовательно, полные реакции в опорах A и B представляют суммы:
и образуют с ними коллинеарные векторы. Следовательно, полные реакции в опорах A и B представляют суммы:
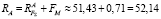 (кН), (3)
(кН), (3)
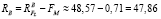 (кН). (4)
(кН). (4)
Итак, констатируем, что результаты решения задачи – ответы равенств (1) и (3), (2) и (4), полученные традиционным и описанным выше способом, – одинаковые.
Аналитические зависимости для реактивных сил RA и RB на основе предложенного метода применительно к рассматриваемой задаче по исходным данным записываются выражениями
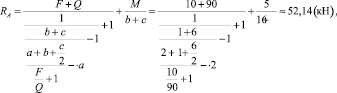 (5)
(5)
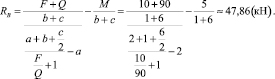 (6)
(6)
Анализ существующих материалов показал, что предложенный метод определения реакций связей двухопорных балок путем последовательных преобразований и уравновешиванием сначала силовой, а затем моментной внешней нагрузки отечественными [4–8 и др.] и зарубежными – американскими [9–11 и др.] и немецкими [12; 13 и др.] – авторами учебно-методической литературы не описан.
Обобщая сказанное, отмечаем, что в рассмотренном способе решения анализируемого вида учебных задач статики можно выделить следующую последовательность: I этап – преобразование распределенных нагрузок в сосредоточенные силы. Определение равнодействующей активных сил и точки ее приложения; II этап – уравновешивание равнодействующей силы, вызываемыми в ответ реактивными составляющими в опорах балки; III этап – определение главного момента и уравновешивание его парой сил с плечом, равным расстоянию между опорами балки; IV этап – определение полных реактивных сил в опорах балки.
В сравнении с традиционным, описываемый способ решения требует более широкой реализации теоретических положений. Учащийся должен знать и уметь применять:
а) правила преобразования распределенной нагрузки в эквивалентную сосредоточенную силу (I этап);
б) принципы определения и свойства равнодействующей плоской системы параллельных сил (I и II этапы);
в) условия равновесия моментов сил относительно точки (II этап);
г) свойства главного момента и пары сил (III этап);
д) правила сложения коллинеарных векторов сил (IV этап).
При этом предложенный метод остается аналитически независимым от традиционного (классического) способа решения таких задач, что подтверждается различием выражений (1) и (5), (2) и (6), а значит, данные методы альтернативны друг другу. Совокупное использование этих подходов при определении опорных реакций балок создает неопровержимую основу для доказательства правильного или неправильного решения задач.
Заключение
Использование разных методов в решении учебных задач обеспечивает повышение осознанности усвоения учебного материала и способствует углублению связей между теоретическими положениями, их применением в учебных задачах и практических ситуациях, а также становлению опыта исследовательской деятельности, формированию и развитию компетенций, значимых профессионально-личностных качеств обучающихся. Как следствие, более совершенной становится методика обучения будущих техников и технологов решению задач статики в курсе технической механики в организациях СПО.
Подтверждением педагогической результативности является повышение качества профессионального обучения, установленное с помощью разработанной нами методики [14]. Средний балл по технической механике вырос до 3,9…4,4 балла, интегрированные индивидуальные показатели качества обучения поднялись до индекса 3,4...4,2, а индивидуальные рейтинги учащихся достигли 71...87 %. Существенно улучшились умения и качества компетентно и логично рассуждать, аргументировать, разрешать учебные проблемные ситуации, принимать рациональные решения [15]. Диагностика с использованием дихотомической шкалы выявила положительную динамику личностных изменений, которая за семестр по процессуальным критериям составила 17…35 %, а по результативным критериям – 9...16 %.



