Процесс обучения является достаточно сложной, динамической системой. Взаимосвязанные деятельность педагога (преподавание) и деятельность обучающегося (учение) находятся в органическом единстве, всегда предметны и направлены на овладение конкретным содержанием изучаемых предметов. В этой связи обоснованно выделяется и третий компонент процесса обучения – содержание образования. «Под содержанием образования понимают систему знаний, умений и навыков, черт творческой деятельности, мировоззренческих и поведенческих качеств личности, которые обусловлены общественными потребностями и в своей совокупности определяют соответствующий уровень образования» (В.И. Крупич).
Проектирование, организация и проведение учебного процесса, ориентированного на математическое развитие студентов, в рамках реализации ФГОС ВО предполагает усиление внимания к научному описанию структуры процесса обучения и выявления его элемента (структурной единицы). Результаты психолого-педагогических исследований показывают, что содержание обучения в структуре учебной деятельности обучающихся может быть представлено только системой задач [1, с. 5]. Многолетний опыт преподавания дисциплины «Математика» на направлениях подготовки 44.03.01 и 44.03.05 «Педагогическое образование» свидетельствует о возможности формирования целостной системы универсальных знаний, умений и навыков обучающихся, направленной на формирование общекультурных, общепрофессиональных и профессиональных компетенций бакалавра педагогического образования.
Авторами статьи в соответствии с требованиями федеральных государственных образовательных стандартов высшего образования по направлениям подготовки 44.03.01 и 44.03.05 «Педагогическое образование» (уровень бакалавриата) [2, 3] написана серия учебно-методических пособий по математическим дисциплинам, в которых предложен материал по проектированию, организации и проведению учебного процесса, предполагающего математическое развитие студентов. Например, учебно-методическое пособие «Системно-структурная модель преподавания темы «Теория делимости» нацелено на решение задач обеспечения преподавателей методическим инструментарием для проведения лекционных и практических занятий по теме и обучающихся (будущих учителей) методической и математической подготовкой, необходимой для грамотного, творческого обучения и воспитания школьников, для дальнейшей работы по углублению и расширению математических знаний.
В пособии учтены особенности преподавания темы «Теория делимости» с учетом реализации системно-структурного подхода к процессу обучения математике.
В первой части дан анализ основных понятий системно-структурного подхода к процессу обучения математике, обоснованы требования, которым должна удовлетворять система математической подготовки бакалавров, представлен технологический подход к проектированию учебного процесса, ориентированного на математическое развитие обучающихся, на примере темы «Теория делимости». Во второй части авторами пособия предложены: возможная система практических занятий по указанной теме; банк заданий для проведения итоговой контрольной работы; модель учебного процесса по теме, а именно технологическая карта – «паспорт» учебного процесса и специальные программы развития обучающихся. Модель разработана на основе педагогической технологии В.М. Монахова [4, с. 60] и методической концепции технологического подхода к проблеме математического развития обучающихся (Т.М. Сафронова).
Дадим некоторые пояснения к понятиям «технологическая карта» и «специальные программы развития».
Технологическая карта содержит пять взаимосвязанных параметрических компонентов:
– целеполагание – система микроцелей по теме «Теория делимости», которые направлены на результативность учебного процесса, ориентированного на математическое развитие обучающихся. Микроцели определили содержание предложенной диагностики;
– диагностика – система проверочных самостоятельных работ, позволяющая установить достижение (или недостижение) каждой микроцели. Содержание проверочных работ задало содержание, объем, сложность и трудность компонента, дозирование самостоятельной (домашней) работы;
– дозирование самостоятельной (домашней) работы – нормирование и подбор по трудности и сложности домашних заданий для обучающихся. Задания ориентируют обучающихся на разные уровни отметок. При проведении диагностики проверяется достаточность (или недостаточность) дозирования домашних заданий;
– логическая структура – это по существу стратегия учебного процесса, развернутого через систему занятий;
– коррекция – программа деятельности для обучающегося, не прошедшего диагностику.
В целеполагании микроцели сформулированы авторами в форме «знать», «уметь», «владеть». Такие точные формулировки, безусловно, будут понятны обучающимся. Кроме того, образовательные цели сформулированы с учетом развивающих целей.
Система проверочных самостоятельных работ построена по конкретным технологическим правилам [5, с. 67]. Каждая диагностическая работа оценивается следующим образом: выполнены только первое или второе задание – обучающийся попадает в группу коррекции; выполнены два первых задания – отметка «удовлетворительно»; выполнены первые три задания – отметка «хорошо»; выполнены все задания – отметка «отлично».
В технологической карте показано, как через систему практических занятий реализуются специальные программы развития: алгоритмического мышления, логического мышления, памяти, речи. В этой связи отметим, что говоря о математическом развитии обучающихся, мы подразумеваем развитие интеллектуальной и мотивационной сфер личности обучающегося с учетом деятельностного подхода в обучении.
Обязательным условием является ознакомление обучающихся с содержанием технологической карты. Это позволяет:
преподавателю:
– рассматривать обучающихся как равноправных участников учебного процесса по учебной теме (заранее объявлены образцы диагностических самостоятельных работ);
– учитывать их индивидуальные особенности;
– нормировать процесс обучения (норма нагрузки, норма требований, норма оценок);
обучающемуся:
– увидеть четкую и рациональную систему требований к его знаниям и умениям;
– выстроить индивидуальную траекторию достижения образовательных и развивающих целей и выбрать целевой ориентир отметки (соответствующий ценностным установкам обучающегося).
Заметим, что ТК, включая в себя все основные компоненты учебного процесса, не дает конкретной информации о занятии. Поэтому модели (проекты) практических занятий по теме «Теория делимости» также разработаны и предложены авторами в настоящем пособии.
Практические занятия направлены на закрепление теоретического материала на практическом уровне. Для подготовки к занятию студенту необходимо разобрать материал, изложенный на лекции, выучить определения и формулировки теорем, разобрать примеры и задачи, которые приводились преподавателем. Для этого используются: конспекты лекций, соответствующие разделы печатных и электронных учебников авторов статьи.
В пособии приведена возможная система практических занятий по теме «Делимость», структурированная не только по содержанию изучаемого материала, но и по сложности приводимых задач, по уровням формируемых компетенций. Каждое занятие содержит вопросы, предназначенные студентам для подготовки к занятию, с указанием литературы, в которой можно найти на них ответы, образцы решения стандартных задач, перечень заданий для рассмотрения на практическом занятии и перечень задач для самостоятельного решения. Приведем пример практического занятия из пособия на тему «Простые и составные числа. Решето Эратосфена». Для успешного усвоения темы практического занятия обучающийся должен: знать определения простого и составного числа, свойства простых чисел, теорему Евклида, метод составления таблицы простых чисел; уметь определять, является ли данное число простым, составлять таблицу простых чисел с помощью решета Эратосфена; владеть навыками устных и письменных вычислений, навыками построения математических умозаключений, навыками построения логических рассуждений.
Вопросы для самоподготовки: определения простого и составного числа; свойства простых чисел; теорема Евклида о бесконечности множества простых чисел; метод составления таблицы простых натуральных чисел, не превосходящих данного числа.
Образцы решения задач:
Задача № 1. Из множества {36, 41, 79, 87, 181, 257, 345} выпишите простые числа, а составные разложите на простые множители.
Решение. Согласно определению простого числа надо выбрать из данного множества чисел те, которые имеют только два делителя: единицу и само себя. Используя признаки делимости, устанавливаем, что числа 41, 79, 181, 257 – простые, а числа 36, 87 и 345 – составные: 36 = 2 • 2 • 3 • 3; 87 = 3 • 29; 345 = = 3 • 5 • 23.
Задача № 2. Составить таблицу простых натуральных чисел, не превосходящих 30.
Решение. Так как 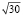 < 6, то простыми натуральными числами меньшими или равными
< 6, то простыми натуральными числами меньшими или равными 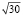 будут 2, 3, 5. Выпишем подряд все натуральные числа от 2 до 30:
будут 2, 3, 5. Выпишем подряд все натуральные числа от 2 до 30:
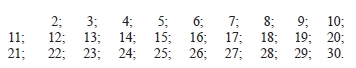
Вычеркнем в (1) каждое второе число после двух (т.е. вычеркнем числа, кратные двум, кроме числа 2):
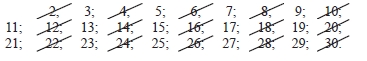
Затем аналогично вычеркнем каждое третье число после трех и каждое пятое число после пяти. Все оставшиеся числа будут простыми числами, не превосходящими 30. Это числа 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Задача № 3. Не пользуясь таблицей простых чисел, установить, являются ли простыми числа 223 и 1287.
Решение. Так как 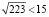 , то выпишем все простые числа, не превышающие 15: 2, 3, 5, 7, 11, 13. Используя признаки делимости, устанавливаем, что
, то выпишем все простые числа, не превышающие 15: 2, 3, 5, 7, 11, 13. Используя признаки делимости, устанавливаем, что 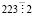 ,
, 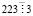 ,
, 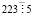 . Чтобы выяснить делится ли 223 на 7, 11 и 13, выполним деление углом:
. Чтобы выяснить делится ли 223 на 7, 11 и 13, выполним деление углом:
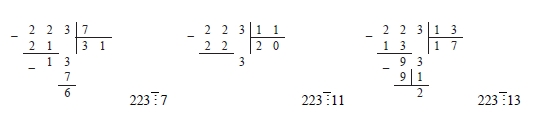
Следовательно, 223 – простое число. Так как 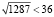 , то выпишем все простые числа, не превышающие 36: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31.
, то выпишем все простые числа, не превышающие 36: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31.
Используя признаки делимости, устанавливаем, что 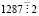 ,
, 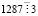 ,
, 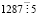 . Чтобы выяснить делится ли 1287 на 7, 11, 13, 17, 19, 23, 29, 31, выполним деление углом:
. Чтобы выяснить делится ли 1287 на 7, 11, 13, 17, 19, 23, 29, 31, выполним деление углом:
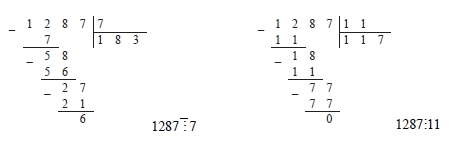
Следовательно, 1287 – составное число.
Задача № 4. Доказать, что число 65 – 92 является составным.
Доказательство. Разложим данное число на множители: 65 – 92 = 25•35 – 34 = 34(25•3 – 1). Число 65 – 92 имеет по крайней мере еще два делителя 34 и 25•3 – 1, отличные от единицы и самого числа, поэтому оно составное.
Задачи для решения на практическом занятии:
1. Из множества чисел {13, 27, 29, 51, 67, 213, 281} выписать простые числа, а составные разложить на простые множители.
2. Может ли сумма двух простых чисел быть простым числом? Привести примеры.
3. С помощью решета Эратосфена найти все простые числа, не превосходящие 40.
4. Не пользуясь таблицей простых чисел, установить, являются ли простыми следующие числа: 139, 331, 377, 819, 571.
5. Доказать, что следующие числа являются составными:
1) 15172 – 15162; 2) 106 – 57; 3) 230 – 1;
4) 64 – 35; 5) 178672 – 159442; 6) 233 + 1.
Задачи для самостоятельной (домашней) работы:
6. Составить таблицу простых натуральных чисел, не превосходящих 50.
7. Не пользуясь таблицей, установить, являются ли простыми числа 269, 461 и 381.
8. На множестве Х = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} задано отношение «иметь одно и то же число делителей». Является ли оно отношением эквивалентности?
9. Доказать, что следующие числа являются простыми:
1) 36 + 65; 2) 12562 – 12552; 3) 533 – 1.
10. Доказать, что трехзначное число, записанное тремя одинаковыми цифрами, делится на 37.
Необходимо отметить, что аналогичную структуру имеют все практические занятия. Приведем соответствующие участки технологической карты.
|
Целеполагание знать: определения простого и составного числа, свойства простых чисел, теорему Евклида, метод составления таблицы простых чисел; уметь: определять, является ли данное число простым, составлять таблицу простых чисел с помощью решета Эратосфена; владеть: навыками устных и письменных вычислений, навыками построения математических умозаключений, навыками построения логических рассуждений. |
Диагностика 1. Из множества чисел {5; 18; 29; 39; 47; 201} выпишите простые числа, а составные разложите на простые множители. 2. С помощью решета Эратосфена найдите все простые числа, не превосходящие 75. 3. Не пользуясь таблицей, установите, являются ли простыми числа 557, 413, 691, 671. 4. 1) докажите, что: а) число 20372 – 20362 является простым. б) число 21132 – 21122 является составным. 2) пусть р1 и р2 – два последовательных нечетных простых числа и |
Коррекция Теоретическая база: [1, §5–7]: 1. Определения простого и составного числа. 2. Свойства простых чисел. 3. Теорема Евклида о бесконечности множества простых чисел. 4. Метод составления таблицы простых натуральных чисел, не превосходящих данного числа. Программы развития: «Мышление» (№ 1), «Мышление» (№ 2), «Память», «Речь». |
||
|
Дозирование самостоятельной (домашней) работы |
||||
|
удовлетворительно: № 6 |
хорошо: № 7 |
отлично: № 8, 9, 10 |
||
В логическую структуру учебного процесса по теме «Теория делимости» «встроены» специальные программы развития: алгоритмического мышления («Мышление» № 1), логического мышления («Мышление» № 2), памяти, устной и письменной речи. В каждой из них предложено теоретическое обоснование целесообразности применения программы, а также примеры задач для практических занятий, которые позволят решать поставленные задачи развития и получать конкретные запланированные результаты. Коротко обозначим цели и содержание разработанных авторами специальных программ развития.
Цель программы развития «Мышление» (№ 1) заключается в том, чтобы в рамках учебной темы «Теория делимости» дисциплины «Математика» спланировать систематическую работу преподавателя по развитию алгоритмического стиля мышления у обучающихся.
Развитию алгоритмического стиля мышления у обучающихся способствуют:
- задачи, связанные с выполнением заданий по алгоритму (например, «с помощью решета Эратосфена найдите все простые числа, не превосходящие 40»);
- задачи, связанные с выработкой последовательности действий с обоснованием (например, «из множества {36, 41, 79, 87, 181, 257, 345} выпишите простые числа, а составные разложите на простые множители»);
- задачи на составление и апробацию алгоритмов (например, «найти все общие делители чисел 35 и 90»);
- задачи, связанные с конструированием алгоритмов (например, «с помощью признака делимости Паскаля вывести признак делимости на 11, 3, 4, 25,13»).
Цель программы развития «Мышление» (№ 2) заключается в том, чтобы в рамках учебной темы «Теория делимости» дисциплины «Математика» спланировать систематическую работу преподавателя по развитию логического мышления у обучающихся.
Приведем примеры задач, способствующих развитию логического мышления обучающихся:
- Докажите, что число 5 не является делителем числа 21.
- Исходя из признака делимости на составное число, вывести признак делимости на 12.
В основу специальной программы развития «Память» были положены следующие принципы:
- Обязательное сочетание непроизвольного и произвольного запоминания.
- Запоминание учебного материала должно проходить осмысленно. Запомнить – значит, прежде всего, понять.
- Память работает активно, если в учебном процессе активно работает ум (активизация мыслительной деятельности обучающихся).
- Постоянное побуждение обучающихся к мнемическим действиям (мнемические процессы: запоминание, сохранение информации, узнавание и ее воспроизведение).
Реализация указанных принципов на каждом практическом занятии позволяет преподавателю целенаправленно работать над развитием основных мнемических процессов.
Цель программы развития «Речь» заключается в том, чтобы в рамках учебной темы «Теория делимости» дисциплины «Математика» спланировать систематическую работу преподавателя по развитию математического языка и математической (устной и письменной) речи обучающихся.
Развитию математического языка и математической речи способствуют:
- задачи, связанные с чтением многозначных натуральных чисел с неизвестными единицами некоторых классов;
- задачи, связанные с записью условий и доказательств математических утверждений, с использованием математических символов;
- задачи, связанные с чтением математических утверждений, записанных с помощью математических символов, а также с записью доказательств этих утверждений, с использованием математических символов;
- задачи, связанные с логическим мышлением, с характером и особенностями математической аргументации и доказательством утверждений;
- задачи, связанные с усвоением математической терминологии.
«Любая деятельность может быть либо технологией, либо искусством… С искусства все начинается, технологией заканчивается, чтобы затем все началось сначала…», – писал В.П. Беспалько в книге «Слагаемые педагогической технологии». Нельзя не согласиться. Планирование, проектирование, организация и проведение учебного процесса, ориентированного на математическое развитие студентов, неизбежны в современных условиях.




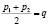 . Докажите, что число q составное.
. Докажите, что число q составное.