При решении обратных задач диагностики знание магнитных характеристик ферромагнитных материалов является необходимым условием. Чаще всего в качестве магнитной характеристики, подлежащей диагностике, используется основная кривая намагничивания (ОКН) B(H). Ввиду того, что различные участки магнитопровода ЭУ намагничиваются по-разному, требуется информация о координатах точек ОКН в диапазоне от нулевого магнитного поля до насыщения. Таким образом, необходимо хранить большой массив данных о координатах точек ОКН (экспериментальные исследования показали, что необходимо использовать массив не менее чем из 1000 точек) или представить этот массив в виде аналитического выражения. Кроме того, ОКН обладает явно выраженной нелинейностью. Недостатки существующих методов определения магнитных характеристик требуют разработки новых эффективных подходов, позволяющих уменьшить время решения обратной задачи и упростить процедуры обработки данных.
Одним из возможных решений поставленной задачи является представление магнитной характеристики в виде аппроксимирующей функции, наиболее точно описывающей ее форму. К аппроксимирующим функциям предъявляются определенные требования [1].
Большое количество работ посвящено применению различных аппроксимирующих выражений для описания магнитных характеристик электротехнических изделий. Проведены сравнения этих выражений между собой применительно к различным магнитным материалам [2–4]. Анализ этих работ показывает, что универсального аппроксимирующего выражения нет. Для разных видов материалов, для разных задач требуется выбор своей аппроксимирующей функции.
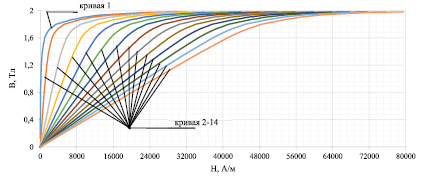
Рис. 1. Основные кривые намагничивания
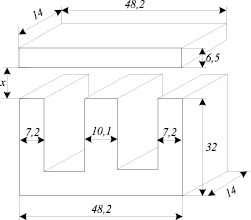
Рис. 2. Конструкция магнитопровода
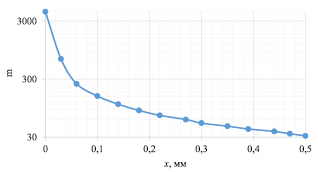
Рис. 3. Изменение магнитной проницаемости магнитопровода
Так при определении ОКН методом решения обратной задачи гармонического баланса [5–7] удобно использовать степенную полиномиальную функцию, состоящую из членов с нечетными степенями вида
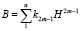 , (1)
, (1)
где B – магнитная индукция, H – напряженность магнитного поля, k2m-1 – коэффициенты аппроксимации, 2n – 1 – максимальная степень полинома.
Погрешность, с которой степенной полином аппроксимирует ОКН, определяется количеством членов степенного ряда, т.е. значением n.
Исследуем зависимость погрешности аппроксимации ОКН от количества слагаемых полинома для магнитных материалов с различной максимальной пронициаемостью. Для этого, используя ОКН электротехнической стали 3411 (кривая 1 на рис. 1) и модель Джилса – Аттертона [8–10] рассчитаны ОКН ряда магнитных материалов с различной относительной магнитной проницаемость m. (кривые 2–14 на рис. 1). Эти ОКН получены в программном пакете ANSYS путем изменения зазора x в Ш-образном магнитопроводе (рис. 2) в диапазоне от 0 до 0,5 мм. с шагом 0,03 мм. При этом относительная магнитная проницаемость m изменялась от 4379 до 32 соответственно. (Характер изменения m представлен на рис. 3).
Результаты аппроксимации оценивались по погрешности [11], вычисленной как расстояние между исходной ОКН и кривой, полученной по аппроксимирующему выражению (1).
Для определения коэффициентов k2m-1 выражения (1) проводилось получение аппроксимации полученных ОКН в программном пакете Statistica, а для расчета погрешности – программа [12], разработанная авторами. В табл. 1 представлены результаты этих исследований.
Из табл. 1 видно, что использовать степенной полином в качестве аппроксимации магнитных характеристик можно, когда магнитная проницаемость не превышает 250 (для критерия была взята погрешность, допустимая ГОСТ для магнитных измерений ±3 %).
При решении задач моделирования работы исполнительных электромагнитов [13, 14] требуется знать ОКН для различных положений якоря:
B = f (H, x), (2)
где x – немагнитный зазор.
В таких задачах аппроксимирующее выражение в виде степенного полинома (1) неприемлемо, в нем отсутствует вторая независимая переменная x.
Используя семейство ОКН (рис. 1), построена зависимость магнитной индукции от зазора в магнитопроводе при различных значениях напряженности магнитного поля (рис. 4).
Представленные на этом рисунке кривые были аппроксимированы с помощью программного пакета Statistica выражениями
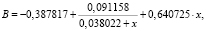
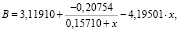
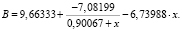
Таблица 1
Погрешность аппроксимации
|
Магнитная проницаемость |
4379 |
674 |
250 |
154 |
111 |
87 |
71 |
60 |
52 |
46 |
42 |
38 |
34 |
32 |
|
Степень полинома |
||||||||||||||
|
3 |
71,72 |
58,12 |
38,12 |
26,77 |
21,59 |
17,37 |
14,01 |
11,33 |
9,17 |
7,42 |
5,98 |
4,78 |
3,78 |
2,93 |
|
5 |
67,27 |
47,73 |
23,42 |
15,48 |
10,14 |
6,42 |
3,82 |
2,51 |
2,96 |
3,16 |
3,20 |
3,12 |
2,97 |
2,78 |
|
7 |
63,12 |
39,01 |
15,01 |
7,95 |
3,68 |
3,68 |
2,93 |
2,81 |
2,46 |
2,14 |
1,89 |
1,78 |
1,62 |
1,42 |
|
9 |
59,83 |
32,01 |
10,05 |
3,45 |
2,67 |
2,60 |
2,15 |
1,75 |
1,47 |
1,18 |
0,88 |
0,72 |
0,73 |
0,82 |
|
11 |
57,38 |
26,19 |
6,78 |
2,02 |
2,35 |
1,88 |
1,31 |
0,91 |
0,65 |
0,79 |
0,85 |
0,80 |
0,69 |
0,63 |
|
13 |
55,11 |
21,31 |
4,07 |
2,02 |
1,83 |
1,22 |
0,75 |
0,74 |
0,79 |
0,65 |
0,56 |
0,50 |
0,44 |
0,38 |
|
15 |
53,11 |
18,56 |
2,19 |
1,91 |
1,30 |
0,70 |
0,75 |
0,67 |
0,53 |
0,46 |
0,37 |
0,31 |
0,31 |
0,31 |
Кривые на рис. 4 имеют сильные отличия друг от друга, но описываются аппроксимирующими выражениями вида
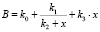 ,
,
что указывает на наличие общих закономерностей у них.
Используя метод размагничивающего фактора [15], можно определить ОКН B1(H1) зная значение зазора в магнитопроводе и ОКН магнитного материала B(H) из которого он изготовлен.
Известно, что коэффициент размагничивания пропорционален значению магнитного зазора и сильно влияет на наклон ОКН магнитопровода [12]:
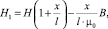
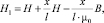
где l – средняя магнитная линия и отсюда
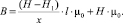
Используя вид последнего выражения, авторами предлагается аппроксимирующее выражение, учитывающее зависимость магнитной индукции от напряженности магнитного поля и зазора магнитопровода:
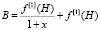 , (3)
, (3)
с учетом зависимости B(H), заданной в виде полинома (1):
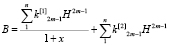 . (4)
. (4)
Для предложенной аппроксимации (4) рассчитана погрешность для полиномов третьей, пятой и седьмой степеней. В табл. 2 представлены результаты этих исследований.
Из табл. 2 видно, что выражению (4), описывающему зависимость магнитной индукции от напряженности и зазора в магнитопроводе, свойственны такие же значения погрешности, что и выражению (1), описывающему зависимость магнитной индукции только от напряженности (см. табл. 1). Таким образом, можно утверждать, что предложенный вид аппроксимирующей функции семейства ОКН (3) удачен, однако требует удвоения количества коэффициентов аппроксимации k2m-1. Поэтому степенной полином нельзя считать удачной функцией для аппроксимации семейства ОКН.
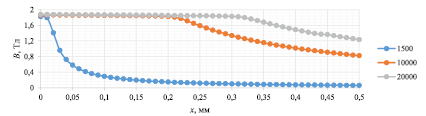
Рис. 4. Зависимость магнитной индукции от зазора в магнитопроводе при различных значениях напряженности магнитного поля
Таблица 2
Погрешность аппроксимации
|
Магнитная проницаемость |
4379 |
674 |
250 |
154 |
111 |
87 |
71 |
60 |
52 |
46 |
42 |
38 |
34 |
32 |
|
Степень полинома |
||||||||||||||
|
3 |
72,22 |
58,53 |
38,39 |
26,96 |
21,74 |
17,49 |
14,11 |
11,41 |
9,23 |
7,47 |
6,02 |
4,81 |
3,81 |
2,95 |
|
5 |
67,74 |
48,06 |
23,58 |
15,59 |
10,21 |
6,46 |
3,85 |
2,53 |
2,98 |
3,18 |
3,22 |
3,14 |
2,99 |
2,80 |
|
7 |
63,56 |
39,28 |
15,12 |
8,01 |
3,71 |
3,71 |
2,95 |
2,83 |
2,48 |
2,15 |
1,90 |
1,79 |
1,63 |
1,43 |
Таблица 3
Погрешность аппроксимации
|
Магнитная проницаемость |
4379 |
674 |
250 |
154 |
111 |
87 |
71 |
60 |
52 |
46 |
42 |
38 |
34 |
32 |
|
Погрешность, % |
8,65 |
4,90 |
3,91 |
4,25 |
4,29 |
4,23 |
4,13 |
4,02 |
3,90 |
5,01 |
5,41 |
5,16 |
5,92 |
5,68 |
Таблица 4
Погрешность аппроксимации
|
Магнитная проницаемость |
4379 |
674 |
250 |
154 |
111 |
87 |
71 |
60 |
52 |
46 |
42 |
38 |
34 |
32 |
|
Погрешность, % |
8,71 |
4,93 |
3,94 |
4,28 |
4,32 |
4,26 |
4,16 |
4,04 |
3,93 |
5,05 |
5,44 |
5,20 |
5,96 |
5,71 |
Меньшее количество коэффициентов аппроксимации ki требуется при использовании выражений на основе арктангенса:
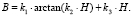 (5)
(5)
В табл. 3 приведены погрешности аппроксимации этим выражением семейства ОКН (рис. 1).
Из табл. 3 видно, что погрешность для всех магнитных проницаемостей не превысила 9 %, что позволяет использовать такую функцию при решении задач методом натурно-модельного эксперимента [5, 14].
Как и в случае степенного полинома, необходимо построить зависимость магнитной индукции не только от напряженности магнитного поля, но и от немагнитного зазора. Для этого, используя выражение (3) и функцию арктангенса (5), получим выражение
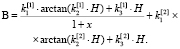 (6)
(6)
Полученная аппроксимация (6) имеет всего шесть коэффициентов ki, что существенно меньше, чем при применении аппроксимации вида (4).
Определены значения погрешностей аппроксимации выражением (6), они приведены в табл. 4.
Результаты, приведенные в табл. 4, как и результаты табл. 3, показывают, что учет зависимости от зазора не приводит к существенному увеличению погрешности.
Применение аппроксимирующих функций способствует повышению скорости решения задачи диагностики электротехнических устройств, путем упрощения процедуры обработки данных за счет использования аппроксимирующего выражения вместо объемных массивов данных. Полученные аппроксимирующие выражения (1), (4), (5) и (6) применимы при определении магнитных характеристик решением обратной задачи гармонического баланса методом натурно-модельного эксперимента, однако для задач, где допустима погрешность до 10 %, предпочтительнее выражения (5) и (6), требующие меньшего количества коэффициентов аппроксимации ki для достижения указанной точности.



