Современные системы в различных предметных областях состоят из большого количества элементов и связей между ними, практически каждый элемент имеет много аналогов, при этом каждый аналог может обладать разным количеством свойств и параметров функционирования. Поэтому как на процессе проектирования, так и на этапах функционирования систем появляется необходимость в интеллектуальной поддержке при подборе структуры системы и параметров функционирования компонентов. Такого рода задачи относятся к предметной области структурно-параметрического синтеза. В настоящее время существует множество методов, которые позволяют проводить структурный и параметрический синтез в отдельности, но методов, способных объединить поиск структуры системы и параметров функционирования ее элементов недостаточно. Поэтому создание новых моделей и методов, базирующихся на современных и хорошо зарекомендовавших себя математических аппаратах, в данном направлении является актуальным.
Для интеллектуальной поддержки структурно-параметрического синтеза больших дискретных систем в настоящее время стали использовать эвристические алгоритмы. Данный подход не гарантирует нахождения точного решения (или оптимального), но при этом проведенные ими вычисления являются достаточными. Кроме того, такого рода алгоритмы дают возможность значительно уменьшить время, требуемое для нахождения хорошего решения.
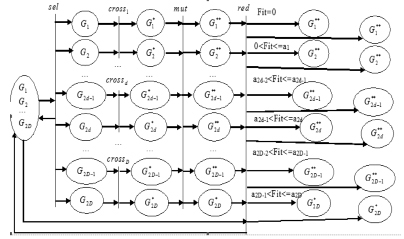
Рис. 1. Модель генетического алгоритма на основе вложенной сети Петри
Одним из представителей эвристических методов является генетический алгоритм (ГА). Эффективность работы данного подхода раскрыта в большом количестве публикаций, как отечественных, так и зарубежных. Несмотря на кажущуюся простоту функционирования ГА стоит отметить, что в настоящее время разновидность операторов, работающих с виртуальной популяцией, достаточно много и практически у каждого оператора имеются свои параметры работы. Данные параметры позволяют увеличивать либо уменьшать разрушающую способность оператора, что в свою очередь влияет на «перемещение» популяции в области поиска решений.
При использовании ГА общепринятой практикой считается определение операторов и выставление параметров их функционирования. Как правило, эти настройки выполняются экспертом на основе ряда вычислительных экспериментов и собственного опыта работы как с ГА, так и в предметной области. При этом стоит отметить, что не всегда выставленные параметры дают возможность интеллектуальной системе работать достаточно эффективно. К примеру, в области структурно-параметрического синтеза можно сказать, что изменения в элементной базе, на основе которой проводится процедура синтеза, значительно влияют на работу адаптированного ГА. Поэтому можно говорить о том, что управление работой операторов ГА в процессе поиска решения – это актуальная задача, которая направлена на повышение эффективности применения данного подхода.
В данной работе предлагается использовать искусственные нейронные сети (ИНС) в качестве инструментального средства для решения задачи управления ГА. В современных исследования принято использовать ГА для обучения ИНС. Математический аппарат ИНС достаточно хорошо зарекомендовал себя для решения «классической» для данного подхода задачи распознавания образов [1]. Поэтому в данной статье предлагается настроить работу ГА таким образом, чтоб применение ИНС было максимально упрощено.
Так как одной из задач является сведение к минимуму вмешательства эксперта в работу интеллектуальной системы по структурно-параметрическому синтезу больших дискретных систем, то предлагается использовать рекуррентные ИНС.
Применение данного класса сетей обусловлено тем, что при управлении работой ГА требуется учитывать предыдущее состояние популяции, т.е. состояние виртуальной популяции в процессе поиска решений, как до изменения параметров функционирования операторов, так и после. При анализе данного класса сетей был сделан выбор в пользу ИНС Элмана, так как в отличие от других ИНС в ней существует возможность хранения предыстории во внутренней памяти ИНС.
В работах [2] была проведена адаптация ГА к решению задачи структурно-параметрического синтеза с помощью теории сетей Петри. Это было обусловлено тем, что данный математический аппарат обладает свойством параллелизма и получил достаточное количество расширений, чтобы моделировать не только процесс синтеза, но и элементную базу в различных предметных областях.
Для моделирования работы ГА применяется такой вид сетей Петри, как вложенные сети Петри. В данном классе сетей метка является сетью и переходы могут быть сетью также. Это свойство и предлагается использовать для моделирования работы ГА. В нашем случае метки верхнего уровня сети будут являться особями популяции и представлять модели синтезируемой системы, а переходы будут моделировать работу операторов генетического алгоритма.
В отличие от модели ГА, представленного в вышеуказанной работе, требуется провести его модернизацию для сбора статистической информации, на основе которой и будет принято решение об изменении параметров функционирования операторов генетического алгоритма ИНС. Данная модернизация представлена на рис. 1.
В данной модели выделены отдельные слои позиций, которые служат для сбора статистики по значению функции приспособленности для каждой особи и сбору количества особей с одинаковым значением функции приспособленности.
Проведем моделирование ИНС Элмана в соответствии с представленной выше моделью ГА. Для этого предлагается использовать другое расширение сетей Петри, которое наиболее подходит к решаемой задаче, а именно информационные сети Петри (ИСП).
Отличием этого расширения сетей Петри от других является то, что метка не является атомарным элементом, а представляет собой вещественное число в диапазоне от 0 до 1 [3–6]. Это свойство предлагается использовать при моделировании искусственной нейронной сети. Оно позволит устанавливать пороги срабатывания для моделирования работы нейрона и позволит изменять пороги срабатывания на основе модели внутренней памяти нейронной сети.
С помощью ИСП проведем моделирование нейрона в ИНС Элмана (см. рис. 2).
- In1, In2, In3 – входы нейрона;
- Out1 – выход нейрона;
- k1, k2, k3 – коэффициент усиления (согласно теории информационных сетей Петри);
- In4 – const (порог срабатывания нейрона).
На рис. 3 показана реализация памяти для ИНС Элмана.
- In1 – вход;
- In2 – вход тактового сигнала (сигнал запоминать);
- Out1 – выход с задержкой в один шаг;
- Out2 – выход с задержкой в два шага.
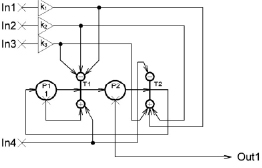
Рис. 2. Модель нейрона Элмана на основе информационных сетей Петри
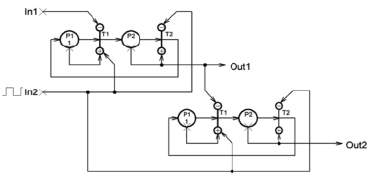
Рис. 3. Модель памяти для нейронной сети Элмана на основе информационной сети Петри
Представленная модель ИНС Элмана и модель внутренней памяти, выполненная с использованием математического аппарата ИСП, будет способна к управлению работой модели ГА для структурно-параметрического синтеза больших дискретных систем с заданным поведением, а также к самообучению. Самообучение ИНС Элмана заключается в подборе значений коэффициентов передачи информационных дуг. Информационные дуги будут реализовывать требуемые функциональные зависимости между входными и выходными значениями модели ИНС.
Представленная модель ИНС на основе ИСП потребует провести обучение, после него она сможет принимать решение по изменению параметров функционирования операторов ГА.
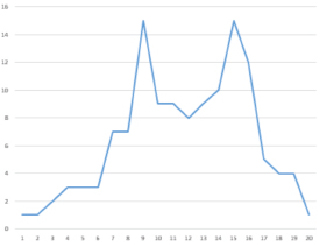
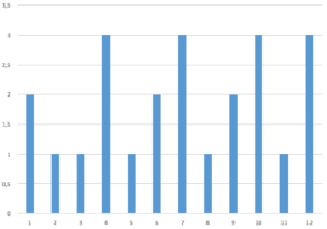
Для работы ИНС предлагается использовать «классическую» задачу распознавания изображений. Для этого следует использовать два изображения, представленные на рис. 4.
На рис. 4, а, по оси у – значение функции приспособленности, по оси х – расположены хромосомы популяции, отсортированные по степени сложности моделей большой дискретной системы с заданным поведением. При сортировке следует учитывать сложность структуры системы (количество элементов, которые в нее входят, сложность элементов, которое устанавливает эксперт, и сложность соединений, также установленную экспертом). Например, модель системы, полученная в результате синтеза, состоящая из одного элемента, будет располагаться ближе к 0, чем модель из двух элементов, если существуют модели с одинаковым количеством элементов, то вступает в силу заранее формализованное с помощью бинарных деревьев мнение эксперта. Если количество элементов и сами элементы одинаковы, то рассматриваются соединения, также формализованные бинарными деревьями, по мнению экспертов. Если модели, полученные в результате синтеза, полностью идентичны, то записывается одна из них.
На рис. 4, б, по оси х – значение функции приспособленности, а по оси y – количество особей популяции с данным значением.
Два этих графика позволят ИНС Элмана принимать управленческое решение, через заранее заданное число обработанных популяций, так как принимать решение на каждой итерации будет нецелесообразно и непрактично.
Для реализации адаптивного управления процедурой структурно-параметрического синтеза больших дискретных систем с заданным поведением следует оценивать два параметра:
1) состояние популяции в целом, которое дает возможность оценить сходимость ГА, а затухание ГА при выставленных параметрах функционирования операторов (Sel, Cross, Mut и Red);
2) значение функции приспособленности каждой особи популяции, что дает возможность находить многоэкстремальность функции и реагировать настройками функционирования операторов ГА соответствующим образом, тем самым ускоряя процесс сходимости ГА.
Для решения задачи структурно-параметрического синтеза больших дискретных систем с заданным поведением ГА можно разделить на 4 этапа:
1) синтез большой дискретной системы на основе элементов системы;
2) синтез большой дискретной системы на основе связей между элементами (межкомпонентная шина);
3) синтез на основе параметров функционирования элементов (функциональные переходы в моделях элементов на основе сетей Петри);
4) синтез на основе начальных состояний элементов, входящих в состав большой дискретной системы (начальная маркировка моделей элементов).
а)
б)
Рис. 4. Изображения для распознавания ситуации нейронной сетью Элмана: а) значение функции приспособленности каждой особи, б) состояние популяции в целом
Таким образом, результирующую схему функционирования адаптивного структурно-параметрического синтеза больших дискретных систем с заданным поведением можно представить так, как показано на рис. 5.
Как видно из представленной схемы, данные о функционировании моделей ГА (в нашем случае это четыре сети Петри), показанные на рис. 1, поступают на ИНС (представленную моделью на основе ИСП), которая в свою очередь принимает решение о соответствующем управлении процессом структурно-параметрического синтеза.
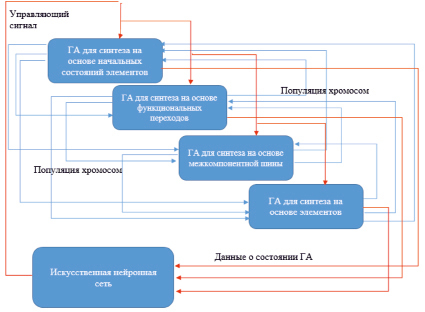
Рис. 5. Схема функционирования адаптивного структурно-параметрического синтеза больших дискретных систем с заданным поведением
Задачи структурно-параметрического синтеза больших дискретных систем довольно трудоемкие, поэтому применение эволюционных методов дает возможность снизить время для поиска решений. Использование ИНС позволит изменять настройки функционирования ГА и своевременно распознавать ситуации, которые позволят изменять режимы функционирования операторов и переключаться между четырьмя моделями. При этом задача распознавания сводится к знакомой задаче распознавания образов, которые состоят из двух графиков (распознавание букв в алфавите). Это даст возможность создать язык для функционирования ГА, что, в свою очередь, позволит ускорить процесс поиска решений.



