Особое место среди дисциплин математического цикла, вошедших в структуру образовательных стандартов нового поколения, занимают теория вероятностей, математическая статистика, теория случайных процессов, а также ряд дополнительных дисциплин, изучаемых студентами на старших курсах бакалавриата или в магистратуре. Вероятностные дисциплины тесно связаны с практикой, имеют большое прикладное значение, поскольку изучают математические модели статистических закономерностей природы. Вероятностные и статистические методы широко используются в технических, технологических, экономических науках. Это связано с развитием массовых процессов в производстве и экономике, с развитием экспериментальной техники и необходимостью проведения более тонкого анализа результатов эксперимента. В настоящее время во всех инженерно-технических, технологических, экономических вузах читается курс теории вероятностей и математической статистики. Даже если не всем инженерам в своей производственной деятельности придется применять вероятностно-статистические методы, то уж во всяком случае, им необходимо познакомиться с основными понятиями и идеями, чтобы понимать соответствующие выводы.
В статье обращается внимание на особенности преподавания и методическое обеспечение дисциплины «Теория вероятностей», учитывая опыт ее изложения в МГТУ им. Н.Э. Баумана [1, 2]. В работе приводится описание структурирования курса «Теория вероятностей» в рамках модульно-рейтинговой системы, принципы формирования фонда оценочных знаний дисциплины, отмечается важность применения математических пакетов при освоении дисциплины в техническом университете.
Цели и задачи дисциплины
Дисциплина «Теория вероятностей» входит в вариативную часть математического и естественнонаучного циклов учебного плана студентов. Количество часов, отведенных на изучение этой дисциплины, варьируется в зависимости от получаемой студентами специализации и для большинства составляет один семестр. Трудоёмкость дисциплины – 2 зачётные единицы. Доли аудиторной и самостоятельной работы в общем объеме часов, выделенных на дисциплину, примерно одинаковы (около 50 %).
В учебном плане большинства специальностей дисциплина «Теория вероятностей» состоит из двух модулей одинаковой трудоемкости: «Случайные события», «Случайные величины. Предельные теоремы»Случайные величины. Предельные теоремы. Каждый модуль предполагает самостоятельное выполнение домашнего задания, а также написание рубежного контроля на семинарских занятиях. Оценка результатов освоения дисциплины проводится на основе модульно-рейтинговой системы [3].
Главными целями изучения дисциплины является приобретение теоретических знаний основных законов теории вероятностей и практических навыков по использованию ее математического аппарата для решения инженерных задач, имеющих прикладную направленность.
Основные задачи освоения дисциплины формулируются следующим образом: ознакомить студентов с теорией множеств, способами вычисления вероятностей случайных событий, понятиями дискретной и непрерывной случайной величины (в том числе в многомерном пространстве), способами качественного и количественного описания и анализа законов распределения, а также их числовых характеристик, основами применения асимптотических методов теории вероятностей. Важным представляется развитие у студента знаний и умений, основанных на использовании описанных методов при решении задач в смежных дисциплинах естественнонаучного и профессионального циклов образовательной программы, способности к аналитическому исследованию прикладных задач, умению построить математическую модель решаемой инженерной задачи.
Для успешного освоения дисциплины «Теория вероятностей» требуется синтез знаний, полученных при изучении дисциплин математического цикла: математического анализа, аналитической геометрии и линейной алгебры, дифференциальных уравнений.
Результаты освоения дисциплины
К результатам изучения дисциплины «Теория вероятностей» отнесем владение терминологией основных разделов дисциплины: случайные события, случайные величины, законы распределения и их числовые характеристики, предельные теоремы (закон больших чисел, центральная предельная теорема); представление о сути и прикладном характере центральных понятий и теорем дисциплины, таких как случайное событие, способы задания вероятности, формула полной вероятности, формула Байеса, дискретная и непрерывная случайная величина, функция распределения, закон распределения, математическое ожидание, медиана, мода, дисперсия, среднее квадратичное отклонение, ковариация, случайный вектор, ковариационная матрица, закон больших чисел, центральная предельная теорема; знание основных вероятностных моделей, используемых при практических исследованиях (например, основные законы распределения и их числовые характеристики и др.), а также способов их построения и верификации; владение методиками решения типовых задач по дисциплине, таких как вычисление классической и геометрической вероятности события, проведение их статистической оценки, использование формул полной вероятности и формулы Байеса, вычисление значений случайной величины, построение ее ряда распределения и функции распределения, вычисление числовых характеристик (математического ожидания, медианы, моды, дисперсии и среднего квадратичного отклонения), использование предельных теорем; умение использовать математические пакеты для решения прикладных задач теории вероятностей.
Цель изучения дисциплины состоит в формировании у студента на основе полученных теоретических знаний, практических навыков и умений, профессиональных компетенций [4], которые позволят будущему инженеру решать многочисленные вероятностные задачи как технического, так и исследовательского характера.
Проблемы обучения
Задачи теории вероятностей существенно отличаются от задач курса математического анализа или линейной алгебры. Основная сложность состоит в переходе от реальной практической задачи к адекватной формальной вероятностной модели. Поэтому на первых этапах изучения дисциплины основное внимание необходимо уделять выработке навыков использования формального аппарата, методике теоретико-вероятностного моделирования реальных задач, технике применения аксиом и теорем теории вероятностей при решении практических задач.
Учебные [1] и методические [2] пособия представляют собой важную составляющую освоения теоретического материала и методов решения прикладных задач. В них должно присутствовать взвешенное сочетание строгости математического изложения теории с прикладной направленностью задач и примеров, иллюстрирующих теоретические положения. Особое внимание должно быть обращено на решение задач прикладного инженерно-технического плана.
Для усвоения полученных теоретических знаний в рамках данного курса организовано проведение компьютерных лабораторных работ, включающих моделирование и численное экспериментирование. Такие работы дополняют, иллюстрируют математическую теорию примерами и реальными расчетами. Данный подход хорошо вписывается в концепцию активного и интерактивного обучения и способствует появлению навыков самостоятельного научного исследования. Однако на проведение лабораторных работ в курсе, который рассчитан на 2 зачетные единицы, большое количество аудиторных часов выделить затруднительно и, фактически, большая часть работы на компьютере выполняется студентами самостоятельно. Поэтому студентам предоставляются подробные методические указания для решения вероятностных задач на ЭВМ с использованием программных пакетов, адаптированных для мобильных устройств, таких как Maple, Mathematica, MATLAB, MATHCad и др. (см. [5–7]).
Оценочные средства
Любой учебный процесс предусматривает своевременный контроль знаний учащихся. Оценка результатов освоения дисциплины «Теория вероятностей» проводится на основе модульно-рейтинговой системы [3], которая стимулирует систематическую работу студентов, позволяет равномерно распределять учебную нагрузку, связанную с самостоятельной работой, в течение всего семестра, снижает роль случайностей при сдаче экзаменов и зачетов, повышает состязательность в учебе.
Авторами разработан комплект контрольно-оценочных средств для проверки знаний учащихся, который предусматривает в каждом из двух модулей рубежный контроль, содержащий один теоретический вопрос и три-четыре задачи на классическое определение вероятности, теоремы сложения и умножения, формулы полной вероятности и Байеса, испытания Бернулли, вычисление числовых характеристик дискретных и непрерывных случайных величин, применение закона больших чисел и центральной предельной теоремы
Наряду с рубежным контролем проводится тестирование студентов. Такая форма текущего контроля позволяет выявить знания студентов, степень их усвоения, понимания пройденного материала и на основе этого строить и совершенствовать технологию преподавания, оперативно устранять пробелы, выявлять трудные места в освоении дисциплины. Тестовые задания не требуют больших затрат времени, дают возможность проверять и закреплять знания студентов в течение всего учебного процесса. Например, для проверки теоретических знаний по модулю 1 предложены тестовые задания из 10 вопросов.
Все предлагаемые контрольные мероприятия нацелены на формирование знаний основных законов и методов теории вероятностей, а также навыков их практического использования.
Приведем примеры заданий рубежного контроля по двум программным модулям, а также тестовые задачи по разделу «Случайные события».
Пример 1. Модуль 1. Случайные события
Задания рубежного контроля
1. Дать определение вероятностного пространства, записать свойства вероятности. Доказать теорему сложения вероятностей.
2. Локационная станция обнаруживает объект в радиусе действия с вероятностью 0,8 при одном цикле. Сколько циклов обследования необходимо провести, чтобы обнаружить объект с вероятностью не менее 0,95?
3. Игральную кость бросают 2 раза. Известно, что в первом опыте выпало четное число очков. Найти вероятность того, что в сумме будет не менее 9 очков.
4. Для некоторого изделия, выпускаемого заводом, установлено, что в среднем на 100 изделий 4 не соответствуют техническим условиям. Для проверки изделия на соответствие техническим условиям на заводе проводится упрощенное испытание. Как показал опыт, «хорошие» изделия проходят это испытание с вероятностью 0,98, «плохие» – с вероятностью 0,05. Какова вероятность того, что изделие, дважды прошедшее испытание, является стандартным?
В качестве контроля по разделу «Случайные события» может быть предложен следующий тест:
А. В следующих заданиях вставьте пропущенные слова или выражения:
1. Случайные события A и B называются ________, если их пересечение пусто.
2. Классическое определение вероятности случайного события предполагает, что число элементарных исходов конечно и все элементарные исходы _________________ .
3. Теорема сложения вероятностей для двух случайных событий имеет вид _____.
4. Количество сочетаний из n элементов по m равно ____________________.
5. Событие, состоящее из элементарных исходов, которые одновременно входят в случайные события A и B, называется их _______________.
Б. В следующих заданиях выберите правильный ответ.
6. Пусть функция f(x1,…,x6) дважды непрерывно дифференцируема. Сколько она имеет различных частных производных второго порядка?
а) 6, б) 12, в) 28, г) 30, д) 36.
7. Игральную кость бросают 3 раза. Чему равна вероятность того, что выпадет 2 герба?
а) 1/2, б) 1/3, в) 3/8, г) 5/8, д) 1.
8. Сколькими способами можно распределить 10 команд спортсменов по жребию на 2 группы?
а) 2, б) 5, в) 20, г) 35, д) 45.
9. Из 5 деталей 1 бракованная. Наудачу берут 2 детали. Чему равна вероятность того, что обе детали годные?
а) 0, б) 1/5, в) 2/5, г) 1/2, д) 3/5.
10. Орудие дважды стреляет по цели, вероятность попадания при первом выстреле 0,6; при втором – на 0,05 больше. Какова вероятность того, что произойдет хотя бы одно попадание?
а) 0,5, б) 0,65, в) 0,71, г) 0,86, д) 0,94.
Студент, успешно выполнявший тестовые задания в течение семестра, получает дополнительные рейтинговые баллы.
Пример 2. Модуль 2. Случайные величины. Предельные теоремы
Задания рубежного контроля
1. Математическое ожидание дискретной случайной величины, его свойства, физический и статистический смысл. Доказать линейность математического ожидания.
2. В ящике 3 белых и 7 черных шаров. Наудачу последовательно берут 4 шара с возвращением. Найти закон распределения числа выбранных белых шаров, вычислить математическое ожидание и дисперсию.
3. Случайная величина ξ распределена по закону Парето, определяемому плотностью распределения вероятностей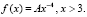 
Найти значение A математическое ожидание и дисперсию случайной величины ξ.
4. Вероятность случайного события 0,54. Сделано 10000 испытаний. Какова вероятность, что наблюденная частота случайного события будет лежать в интервале 0,54 ± 0,01?
Домашние задания и их выполнение с использованием математических пакетов
В современных условиях выполнение типового домашнего задания должно быть нацелено не только на приобретение навыков и знаний из области теории вероятностей, но также на использование компьютера как основного средства поиска информации и решения задач [6, 8, 9]. Поэтому все задачи домашнего задания должны быть решены с использованием прикладных математических программ для численных и аналитических расчетов (Maple, Mathematica, MATLAB, MATHCad и др.). Подробный анализ этих пакетов и методики их использования приведен в [10].
Авторами разработаны варианты домашних заданий по двум модулям, а также демонстрационные варианты, которые разбираются на аудиторных занятиях и выдаются студентам для самостоятельного ознакомления.
Домашнее задание по модулю 1 включает 2 задачи, состоящие из нескольких отдельных заданий. Выполнение домашнего задания № 1 формирует у обучающихся твердые теоретические знания основных понятий и законов из раздела «Случайные события», способствует приобретению практических навыков по их применению, а также умению использовать математические пакеты для решения математических задач. Домашнее задание № 2 состоит из 6 задач на вычисление законов распределений и числовых характеристик случайных величин, применение центральной предельной теоремы, а также моделирование заданных и найденных параметров распределений.
Приведем примеры типовых домашних заданий и решение некоторых из них с применением прикладных математических пакетов (система Wolfram Mathematica [11–14]).
Пример 3. Модуль 1. Случайные события
Вариант типового домашнего задания
Задача 1. На отрезке [0;1] наудачу и независимо друг от друга ставят 10 точек. Требуется:
а) найти вероятность того, что в интервал (0,2; 0,8) попадет не менее 8 точек;
б) известно, что не менее трех точек попали в интервал (0,2; 0,8). Какова вероятность того, что всего в этом интервале не более 7 точек?
в) провести моделирование 100 экспериментов, по которым оценить вероятность событий из пунктов а и б.
Решение.
а) Вероятность попадания каждой случайной точки в интервал (0,2; 0,8) не зависит от положения других точек и равна длине этого интервала, т.е. р = 0,6.
Пусть событие А состоит в том, что в интервал (0,2; 0,8) попало не менее 8 точек, а событие Аj – в том, что в (0,2; 0,8) попало j точек,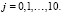 
Тогда 
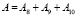, события Аj попарно несовместны и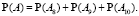 
В силу формулы Бернулли
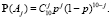
Значит,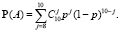 
Вычисления по последней формуле проведем в среде Wolfram Mathematica. Сначала присвоим перемененной p значение 0,6, а затем зададим функцию PA[j], которая будет вычислять вероятность события Аj. C помощью функции Row выведем ответ на пункт а).
(********************************)
(*Вычисление вероятности для пункта а*)
p=0.6;
PA[j_]:=Binomial[10,j]p^j (1-p)^(10-j);
Row[{"P(A)=",Sum[PA[j],{j,8,10}]}]
(*Результат выполнения*)
P(A)=0.16729
(********************************)
б) Пусть события B и С состоят в том, что в интервал (0,2; 0,8) попало не менее 3 и не более 7 точек соответственно. Тогда
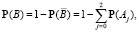
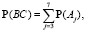
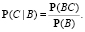
Вычисления в среде Wolfram Mathematica:
(********************************)
(*Вычисление вероятности для пункта б*)
Row[{"P(B|C)=",Sum[PA[j],{j,3,7}]/(1-Sum[PA[j],{j,0,2}])}]
(*Результат выполнения*)
P(B|C)=0.830628
(********************************)
в) Выполнение этого пункта начнем с моделирования 100 экспериментов. Так как координата точки на отрезке [0; 1] – это значение случайного числа из соответствующего диапазона, то будем использовать встроенный в систему Wolfram Mathematica генератор псевдослучайных чисел. С помощью функции RandomReal создадим массив sample из 100 выборок по 10 случайных чисел. Оценку вероятностей построим как отношения числа выборок, в которых осуществились события из пунктов а и б, к числу экспериментов, равному 100. Для этого определим индикаторные функции fA, fB и fBC, соответствующие случайным событиям A, В и С. Применяя их к каждой выборке из массива sample, получим массив объема 100 из нулей и единиц, в котором каждая единица соответствует тому, что для данной выборки произошло соответствующее событие. Для построения оценок остается только сложить элементы полученного массива и разделить на 100. Ниже приведен текст программы и результат ее выполнения, а также фрагмент сгенерированной выборки.
(********************************)
(*Вычисление оценок вероятностей для пункта в*)
sample=RandomReal[{0,1},{100,10}];
fA[s_]:=If[Length[Select[s,0.2<#<0.8&]]>=8,1,0];
fB[s_]:=If[Length[Select[s,0.2<#<0.8&]]>=3,1,0];
fBC[s_]:=If[3<=Length[Select[s,0.2<#<0.8&]]<=7,1,0];
Row[{"Оценка P(A)=",N[Plus@@(fA/@sample)/100]}]
Row[{"Оценка P(B)=",N[Plus@@(fB/@sample)/100]}]
Row[{"Оценка P(BC)=",N[Plus@@(fBC/@sample)/100]}]
Row[{"Оценка P(B|C)=",
N[Plus@@(fBC/@sample)/Plus@@(fB/@sample)]}]
(*Результат выполнения*)
Оценка P(A)=0.2
Оценка P(B)=0.98
Оценка P(BC)=0.78
Оценка P(C|B)=0.795918
(*******************************************)
Задача 2. Упавший самолет может находиться в одной из областей I или II с вероятностями 0,6 и 0,4 соответственно. Для поиска упавшего самолета выделено n вертолетов, каждый из которых может проводить поиски только в одной из областей I или II и обнаруживает упавший самолет с вероятностью 0,7 независимо от остальных вертолетов. Требуется:
а) определить оптимальную процедуру поиска, т.е. выяснить, какое распределение вертолетов по областям максимизирует вероятность обнаружения самолета;
б) найти, чему должно быть равно число вертолетов n, чтобы при оптимальном распределении по областям вероятность обнаружения самолета была не меньше 0,95?
Решение.
а) Для решения задачи воспользуемся формулой полной вероятности. Определим H1 и H2 – события, состоящие в том, что самолет лежит в I или II области соответственно. Очевидно, что события H1 и H2 несовместны,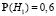 
, 
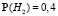. Значит, H1 и H2 образуют полную группу событий.
Обозначим через Ak событие, состоящее в том, что самолет обнаружен при условии, что в I область направлены k вертолетов, 0 ≤ k ≤ n. Тогда
= 
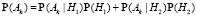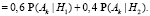
Теперь найдем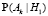 
. Самолет, лежащий в I области, должен быть обнаружен хотя бы одним из вылетевших в эту область k вертолетов, поэтому
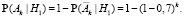
Аналогично,
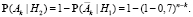
Подставив найденные значения в формулу полной вероятности, получим, что
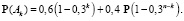
Для ответа на пункт а) задачи нужно найти максимум вероятности P(Ak) по k. Начнем с того, что нарисуем график этих вероятностей при фиксированном значении n. Зададим функцию PA[n, k] для вычисления вероятности P(Ak) и вычислим ее значения при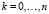 
.
(*******************************************)
(*Построение графика вероятностей для пункта а*)
PA[n_,k_]:=1-0.6 0.3^k-0.4 0.3^(n-k);
pk=Table[{k,PA[5,k]},{k,0,5}];
ListPlot[pk,PlotTheme->"Monochrome",AxesStyle->Thick]
(*Результат выполнения*)
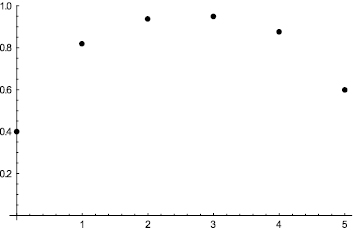
Построение графика вероятностей для пункта а
Из графика видно, как ведут себя вероятности P(Ak) при изменении k. Теперь найдем максимум аналитически. Если максимум P(Ak) достигается при k = K и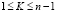 
, то 
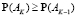и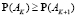 
. Решив вместе два последних неравенства, найдем границы для K. Для этого воспользуемся встроенной функцией Reduce системы Wolfram Mathematica, которая предназначена для решения неравенств. Предварительно каждое из неравенств нужно упростить функцией FullSimplify, а также преобразовать полученный результат при помощи Simplify. Это связано с тем, что по умолчанию все алгебраические неравенства решаются над полем комплексных чисел, нам же нужны только натуральные значения переменной.
(*******************************************)
(*Вычисление значения K для пункта а*)
Reduce[{FullSimplify[PA[n,k]-PA[n,k-1]]>=0,FullSimplify[PA[n,k]-PA[n,k+1]]>=0},k,Reals];
s=Simplify[ %,Assumptions->{n∈Integers}]
(*Результат выполнения*)
–0.331614 + 0.5 n<=k<=0.668386 + 0.5 n
(*******************************************)
Видим, что полученный отрезок имеет единичную длину, откуда следует, что в нем содержится 1 или 2 натуральных числа. Значит, K – это любая целая точка из указанного диапазона. Для иллюстрации полученного результата приведем таблицу, в которой вычислим границы интервалов и значение K (функция kmax[n] используется для вычисления значения K).
(*******************************************)
(*Вычисление значения K для пункта а*)
kmax[n_]:=Floor[0.668386 +0.5 n];
TableForm[Table[{n,s,kmax[n]},{n,5,10}],TableHeadings->{None,{«n»,»Интервал K»,»K»}}]
(*Результат выполнения*)
|
n |
Интервал K |
K |
|
5 |
2.16839<=k<=3.16839 |
3 |
|
6 |
2.66839<=k<=3.66839 |
3 |
|
7 |
3.16839<=k<=4.16839 |
4 |
|
8 |
3.66839<=k<=4.66839 |
4 |
|
9 |
4.16839<=k<=5.16839 |
5 |
|
10 |
4.66839<=k<=5.66839 |
5 |
(*******************************************)
б) Вычислим значение n, при котором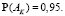 
Для этого воспользуемся функцией FindRoot. В качестве начального приближения возьмем, например n = 2.
(*******************************************)
(*Вычисление вероятности для пункта б*)
FindRoot[PA[n,kmax[n]]==0.95,{n,2}]
n1=Ceiling[n/. %]
(*Результат выполнения*)
{n->4.97532}
5
(*******************************************)
Таким образом, оказывается, что достаточно 5 вертолетов.
Пример 4. Модуль 2. Случайные величины. Предельные теоремы.
Вариант типового домашнего задания
Случайная величина ξ имеет плотность распределения вероятностей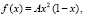 
0 ≤ x ≤ 1 Требуется:
а) найти константу A и функцию распределения;
б) построить графики плотности и функции распределения;
в) найти моду, медиану, математическое ожидание и дисперсию;
г) найти плотность распределения суммы двух независимых случайных величин с плотностью f(x), построить график найденной плотности;
д) пользуясь центральной предельной теоремой, оценить интервал, в котором будет находиться среднее арифметическое 100 значений случайной величины ξ с вероятностью не менее 0,95;
е) смоделировать 20 выборок объема 100 из закона распределения случайной величины ξ и по ним оценить интервал из пункта д.
Рейтинг
По дисциплине «Теория вероятностей» студент, успешно выполнивший все контрольные мероприятия, может набрать от 60 до 100 рейтинговых баллов. На каждый из модулей приходится от 30 до 50 баллов.
Итоговая аттестация по дисциплине проводится в форме распределенного экзамена, окончательная оценка складывается из баллов, набранных студентами в течение семестра в каждом из модулей.
Модуль считается освоенным, если студент выполнил все текущие контрольные мероприятия модуля, набрав по каждому из них не менее установленного минимального балла. При этом оценка за модуль равна сумме баллов за домашнее задание и рубежный контроль. Предусмотрены также премиальные баллы за активную работу на семинарах и выполнение тестовых заданий.
Рубежный контроль состоит их двух частей: сначала проводится контрольная работа в письменной форме по билетам, которые включают теоретические вопросы и задачи, затем ее защита в виде беседы с преподавателем. Все контрольные мероприятия в группах одной специальности проводятся в одни и те же сроки по установленным комплектам заданий и оцениваются по системе, одинаковой для всех групп.
Заключение
Дисциплина «Теория вероятностей», изучаемая в техническом вузе, должна иметь практическую направленность, отражающую не только инженерную специфику обучающихся, но и их специализацию. Этот курс требует специально предназначенного методического обеспечения, включающего наличие справочной литературы, методических пособий и указаний к решению задач, интерактивных учебников, различных иллюстраций выполнения домашних и лабораторных заданий с помощью компьютерной техники и прикладных математических пакетов. Необходимо проводить индивидуальные консультации студентов, добиваясь, чтобы изучаемый ими теоретический материал был творчески, а не механически реализован при решении практически важных технических задач. Представленные в статье результаты педагогических исследований по оптимизации структуры дисциплины «Теория вероятностей» в техническом университете, по наполнению фонда оценочных средств могут быть полезны при решении обозначенных выше проблем совершенствования учебного процесса.