В работе исследована обратная задача определения коэффициентов приведенных жесткостей упругих опор ротора по известным частотам его свободных колебаний. Прямая задача определения частот свободных колебаний ротора на упругих опорах рассматривается во многих трудах по теории колебаний, например [1–4]. Исследования по прямой задаче и постановка обратной спектральной задачи проведены в работе [5], в которой получен метод двойственного определения коэффициентов относительных жесткостей опор ротора по двум известным значениям частот колебаний ротора.
Целью же данной работы является исследование существования и доказательство единственности решения поставленной задачи, а также определение алгоритма решения задачи с учетом не только упругих опор ротора, но и абсолютно жестких закреплений его краев. Приведенный алгоритм решения задачи позволит также определить достаточное число частот колебаний ротора для единственности восстановления приведенных жесткостей его опор.
Задача по свободным поперечно-изгибным колебаниям ротора, как вращающегося стержня на упругих опорах, сводится к решению дифференциального уравнения [1–4]:
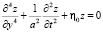(1)
с краевыми условиями
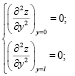
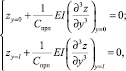(2)
где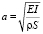 
, 
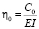, z – перемещение стержня ротора, Спрл, Спрп – приведенные жесткости левой и правой опор ротора соответственно, Е – модуль упругости материала ротора, I – момент инерции поперечного сечения ротора, ρ – плотность материала, S – площадь поперечного сечения ротора, С0 – коэффициент жесткости распределенной опоры, l – длина пролета ротора (рисунок).
В работе [5, c. 135] представлено решение прямой задачи (1), (2) и получено уравнение в виде:
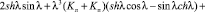
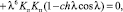(3)
в котором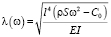 
– собственное значение, ω – частота свободных поперечных колебаний ротора, Kл, Kп – коэффициенты относительной жесткости опор ротора, выражающиеся как
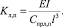(4)
Поставлена и исследована обратная задача идентификации коэффициентов относительной жесткости опор ротора по известным значениям двух частот его поперечных колебаний. Получены аналитические формулы, которые определяют коэффициенты (4) двойственным образом.
В продолжение исследований [5] в данной работе представим другой метод решения обратной задачи, который позволяет учитывать не только упругие опоры, но и возможность определения абсолютно жестких закреплений краев ротора. И в отличие от предыдущего алгоритма решения позволит также доказать единственность определения упругих опор ротора. Для решения такой задачи краевые условия (2) представим в виде
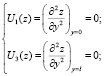
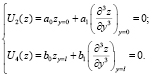(5)
В краевых условиях (2) и (5) коэффициенты связаны соотношениями
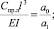
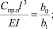
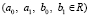. (6)
Модель ротора
Коэффициенты форм U2(z) и U4(z) краевых условий (5) представим в виде элементов следующей матрицы:
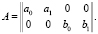
Ненулевые миноры Fij данной матрицы, составленные из столбцов с номерами i и j (i = 1, 2, 3; j = 2, 3, 4), имеют вид
, 
,
, 
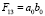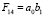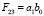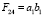. (7)
Тогда обратная задача восстановления коэффициентов условий (5) сводится к нахождению матрицы A c точностью до линейных преобразований ее строк, что равносильно определению линейной оболочки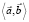 
векторов 
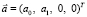и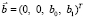 
.
Рассмотрим также краевые условия
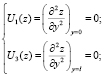
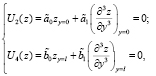(8)
с коэффициентами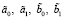 
, отличными от a0, a1, b0, b1. Линейную оболочку на векторах 
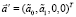и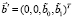 
обозначим как 
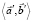. Тогда если наряду с задачей (1), (5) исследовать также задачу (1), (8), то можно сформулировать и доказать следующую теорему, определяющую единственность решения сформулированной выше обратной задачи.
Теорема. Если спектральные задачи (1), (5) и (1), (8) имеют совпадающие ненулевые собственные значения (с учетом их кратностей) и при этом выполняются равенства
, 
,
, 
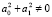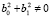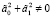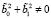, (9)
то совпадают и их линейные оболочки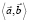 
, 
.
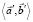Доказательство.
Представление краевых условий задачи в виде (5) требует получения соответствующего частотного уравнения, отличного от уравнения (3). Для этого проведем следующие преобразования.
Известно, что линейно-независимыми решениями уравнения (1) являются функции z1(y) = S(αy), z2(y) = V(αy), z3(y) = U(αy), z4(y) = T(αy), в которых S(αy), V(αy), U(αy), T(αy) – функции Крылова [4, c. 150] от спектрального параметра α = α(ω), где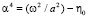 
. Тогда общее решение уравнения (1) представится в виде
= 
.
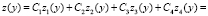
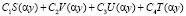Для определения констант C1, C2, C3, C4 воспользуемся краевыми условиями (5) и получим следующую систему уравнений:
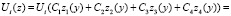
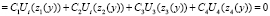, (10)
(i = 1, 2, 3, 4)
Частотное уравнение задачи (1), (5) получим стандартно, учитывая условие существования ненулевого решения системы (10) относительно констант C1, C2, C3, C4, а именно из равенства
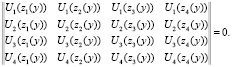(11)
Тогда корни характеристического уравнения (11) будут совпадать со спектральными значениями α = α(ω), содержащими в себе частоту свободных колебаний ротора на упругих опорах.
С учетом условий (5), функций Крылова S(αy), V(αy), U(αy), T(αy) и их производных до третьего порядка включительно, равенство (11) представим в виде
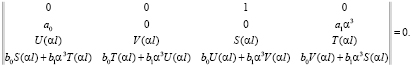
Раскрыв последнее уравнение с учетом функции Крылова и миноров (7) матрицы A получим уравнение
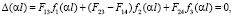(12)
в котором fk(αl) (k = 1, 2, 3) выражаются как
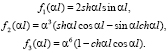(13)
Из свойств общей теории линейных операторов следует, что Δ(αl) является целой функцией порядка ½ [6, c. 46]. Поэтому характеристический определитель Δ(αl) задачи (1), (5) и соответствующий характеристический определитель
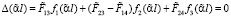(14)
задачи (1), (8) связаны тождественным равенством
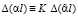, (15)
где K – константа, отличная от нуля.
Отсюда с учетом (9), (12), (14), (15) получаем, что
(16)
С помощью команд математического пакета Maple можно показать, что определитель, составленный из коэффициентов при переменных в разложении функций (13) в степенной ряд, не равен нулю. Откуда следует линейная независимость рассматриваемых функций fk(αl) (k = 1, 2, 3).
С учетом последнего утверждения и из равенства (16) имеем
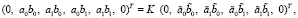(17)
что равносильно пропорциональности бивекторов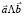 
и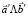 
.
Между классами пропорциональных бивекторов (отличных от нуля) и двумерными подпространствами векторного пространства существует биективное соответствие [7, c. 178]. В этом соответствии каждому подпространству отвечает внешнее произведение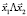 
векторов произвольного его базиса 
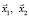, а каждому бивектору 
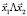– подпространство 
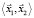. Поэтому из (17) следует, что 
= 
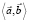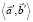. Теорема доказана.
Из теоремы следует, что линейная оболочка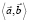 
, построенная на векторах 
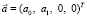и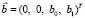 
, восстанавливается единственным образом. Это утверждение, в свою очередь, равносильно единственности решения обратной задачи определения коэффициентов приведенных жесткостей опор ротора.
Построим теперь решение обратной задачи. Пусть α1, α2, α3 – три первые собственные значения задачи (1), (5), являющиеся корнями уравнения (12) и соответствующие первым трем частотам ω1, ω2, ω3 колебаний ротора. Тогда с учетом (15) собственные значения α1, α2, α3 удовлетворяют уравнениям
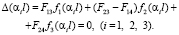(18)
Заметим, что (18) представляют собой систему трех уравнений от четырех неизвестных F13, F14, F23, F24. И как следует из теоремы, эта система имеет единственное решение с точностью до постоянного множителя. По-другому, равенства (18) однозначно с точностью до константы задают бивектор
.
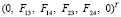Определив таким образом все неизвестные миноры Fij, можно единственным образом восстановить краевые условия спектральной задачи (1), (5).
Применение метода рассмотрим на примерах.
Пример 1. Пусть α1 = 0,9077, α2 = 4,7296, α3 = 7,8531 – собственные значения задачи (1), (5), соответствующие первым трем собственным частотам колебаний ротора при физических параметрах
l = 0,1 м, S = 0,0035 м2, E = 2•1011 Н•м–2,
I = 5•10–6 м4, ρ = 7850 кг•м–3, η = 0,25. (19)
Найдем матрицу A с точностью до эквивалентных матриц, по-другому, определим коэффициенты приведенных жесткостей опор ротора.
Решение. Система (18) при заданных собственных значениях и параметрах (19) перепишется следующим образом:
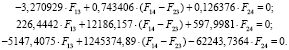
Решение системы:
.
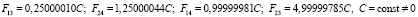Тогда
.
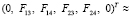
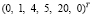Если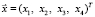 
– произвольный вектор искомой линейной оболочки 
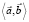, то его координаты удовлетворяют условию
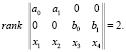
Поскольку, например,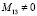 
, то последнее условие равносильно следующим равенствам:
, 
.
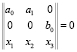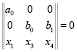Откуда: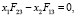 
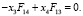
Если, учитывая (7),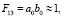 
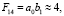
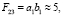то можно считать, что 
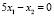и 
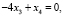тогда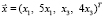 
.
Значит, матрица A имеет вид 
Далее с учетом (6) и (19) найдем соответствующие коэффициенты приведенных жесткостей опор ротора: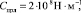 
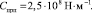
Пример 2. Известны первые три собственных значения
α1 = 3,1416, α2 = 6,2832, α3 = 9,4248
краевой задачи (1), (5) при физических параметрах (19). Определим условия упругих его закреплений.
Решение. Система уравнений (18) в этом случае имеет решение:
.
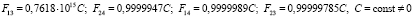Имеем: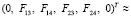 
.
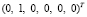Преобразования, аналогичные в примере 1, ведут к следующим приближениям:
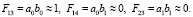
Откуда: 
При этом с учетом равенств (6) и (19) получаем, что коэффициенты приведенных жесткостей опор ротора стремятся к бесконечности, что говорит об абсолютно жестком закреплении обоих краев ротора.
Таким образом, по известным трем частотам поперечно-изгибных колебаний ротора можно определить единственным образом значения коэффициентов приведенных жесткостей левой и правой его опор, в том числе и абсолютно жесткие закрепления.