Исследование движения потока жидкости, содержащей твердые взвешенные частицы, через пористую среду является актуальной задачей для многих областей науки и техники. Задачи вытеснения нефти пластовой и закачанной водой, очистки сточных вод и жидких промышленных отходов, фильтрации питьевой воды требуют изучения процессов переноса и осаждения частиц в пористых средах [1–3].
Пористая среда представляет собой твердое тело, испещренное полыми каналами различной длины и формы, которые называются порами. При закачке в пористую среду суспензии – жидкости с взвешенными твердыми частицами – поток жидкости движется по порам, постепенно заполняя всю пористую среду. Если размеры частиц сравнимы с размерами пор, то твердые частицы проникают вглубь пористой среды. Некоторые частицы, движущиеся по широким порам, беспрепятственно проходят через пористую среду. Другие частицы, которые попали в поры малого поперечного сечения, застревают в них и образуют осадок (рис. 1).
Рассмотрим процесс долговременной глубинной фильтрации, при котором осажденные частицы постепенно накапливаются на всем протяжении пористой среды, а не только в ее поверхностном слое. Предполагается, что одна осажденная частица полностью закупоривает одну пору и прекращает движение через этот канал. Застрявшая в поре частица не может быть выбита из нее другими частицами или потоком жидкости и навсегда остается неподвижной [4]. Основной причиной осаждения твердых частиц суспензии в порах является механико-геометрический механизм захвата частиц: частицы свободно проходят через поры большого диаметра и застревают на входе пор, размеры которых меньше диаметра частиц.
Математическая модель фильтрации состоит из двух дифференциальных уравнений в частных производных первого порядка, описывающих движение твердых частиц в пористой среде. Неизвестными служат концентрации взвешенных и осажденных частиц. Первое уравнение связано с законом сохранения массы частиц, второе задает скорость роста осадка. Коэффициент пропорциональности между скоростью роста осадка и концентрацией взвешенных частиц называется коэффициентом фильтрации. Вид этого коэффициента определяется экспериментально. Если все поры малых размеров закупорены осажденными частицами, процесс образования осадка прекращается и все частицы беспрепятственно проходят через большие поры. Концентрация осажденных частиц достигает максимального значения, при котором коэффициент фильтрации обращается в ноль. Такой коэффициент фильтрации называется блокирующим. В зависимости от кратности корня максимум осадка может достигаться при конечном значении времени или при t → ∞.
Математические модели фильтрации рассматриваются во многих работах. В ряде случаев удается получить точное решение задачи [5–8]. В окрестности линий, на которых построено точное решение, строится асимптотика [9–12]. Если аналитическое решение отсутствует, задача решается численно [13–15].
В работе рассматривается динамика роста осажденных частиц на входе пористой среды. Исследуется решение задачи фильтрации при блокирующих коэффициентах фильтрации различной кратности. Построены графики концентрации осадка для гладких и негладких коэффициентов фильтрации.
Математическая модель
В одномерном случае для однородной пористой среды в предположении постоянных пористости и проницаемости система безразмерных уравнений фильтрации в области 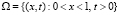 имеет вид
имеет вид
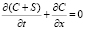 , (1)
, (1)
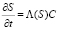 . (2)
. (2)
Здесь C(x, t); S(x, t) – концентрации взвешенных и осажденных частиц. Коэффициент фильтрации 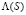 положителен и убывает с ростом S, поскольку при увеличении осадка количество вакантных пор малого размера сокращается и скорость образования осадка уменьшается.
положителен и убывает с ростом S, поскольку при увеличении осадка количество вакантных пор малого размера сокращается и скорость образования осадка уменьшается.
Введение переменной пористости и проницаемости пористой среды существенно усложняет уравнение массообмена (1). Относительные пористость и проницаемость возрастают при увеличении концентрации осажденных частиц S(x, t). Уравнение (1) принимает вид
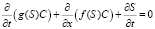 . (3)
. (3)
Здесь пористость g(S) и проницаемость f(S) – гладкие возрастающие функции.
Для единственности решения систем уравнений (1), (2) и (2), (3) необходимо задать дополнительные условия. Пусть в пористую среду впрыскивается суспензия с постоянной концентрацией p взвешенных частиц, а в начальный момент времени пористая среда пуста и не содержит взвешенных и осажденных частиц. Соответствующие условия имеют вид
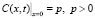 , (4)
, (4)
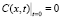 , (5)
, (5)
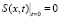 . (6)
. (6)
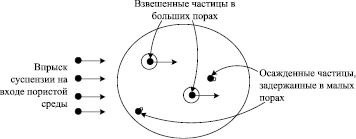
Рис. 1. Сечение пористой среды с взвешенными и осажденными частицами суспензии
Точное решение на входе пористой среды
Подставляя условие (4) в уравнение (2), получаем соотношение для концентрации осажденных частиц на входе пористой среды x = 0
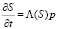 . (7)
. (7)
Решаем уравнение (7) методом разделения переменных. Делим переменные
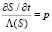 (8)
(8)
и интегрируем (8) по переменной t:
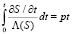 . (9)
. (9)
Используя условие (6), произведем замену в интеграле (9):
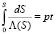 . (10)
. (10)
Соотношение (10) задает зависимость от времени концентрации осажденных частиц на входе пористой среды.
Рассмотрим блокирующие коэффициенты фильтрации, имеющие корень кратности n, вида
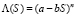 . (11)
. (11)
Здесь a, b, n – положительные константы.
В случае n ≥ 1 интеграл в левой части (10) имеет неинтегрируемую особенность. Решение S(0, t) возрастает при всех t и стремится к предельному значению a/b при t → ∞.
При 0 < n < 1 особенность в интеграле (10) интегрируема, и предельное значение концентрации осадка на входе пористой среды достигается за конечное время tmax, определяемое из соотношения
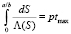 . (12)
. (12)
Ниже приводятся расчеты концентрации осажденных частиц на входе пористой среды и соответствующие графики для различных значений кратности n.
Численное моделирование
Ниже при построении графиков концентрации осажденных частиц при различных значениях кратности n выбраны значения параметров
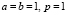 . (13)
. (13)
1. n = 1. Случай линейного коэффициента фильтрации наиболее часто встречается в приложениях. Интеграл в левой части (10) равен
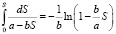 ,
,
и решение уравнения (10) имеет вид
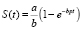 . (14)
. (14)
На рис. 1 приведен график концентрации осадка при n = 1.
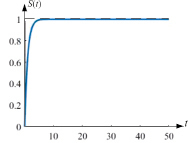
Рис. 2. Концентрация осадка для линейного коэффициента фильтрации
2. n > 1. В случае кратного корня (11) решение уравнения (10) задается формулой
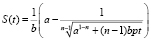 . (15)
. (15)
На рис. 3, 4 приведены графики концентрации осадка при n = 2 и n = 3.
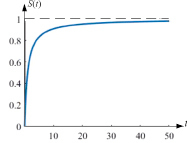
Рис. 3. Концентрация осадка для коэффициента фильтрации при n = 2
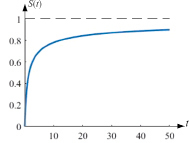
Рис. 4. Концентрация осадка для коэффициента фильтрации при n = 3
3. 0 < n < 1. В случае дробной степени n решение уравнения (10) имеет вид
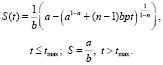 (16)
(16)
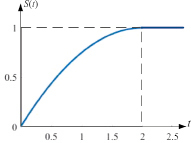
Рис. 5. Концентрация осадка для коэффициента фильтрации при n = 0,5
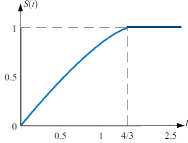
Рис. 6. Концентрация осадка для коэффициента фильтрации при n = 0,25
На рис. 5, 6 приведены графики концентрации осадка при n = 0,5 и n = 0,25.
При n < 1 максимальный осадок достигается в момент времени t = tmax, при t > tmax концентрация осадка постоянна. Имеем
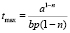 . (17)
. (17)
В частности, для значений параметров (13) при n = 0,5 имеем tmax = 2; при n = 0,25 – tmax = 4/3.
Заключение
При впрыске суспензии в пористую среду процесс фильтрации начинается у входа. В каждый момент времени на входе пористой среды концентрация осажденных частиц максимальна. Подробное изучение динамики осадка на входе позволяет оценить процесс долговременной фильтрации внутри пористой среды.
При уменьшении количества свободных пор малых размеров скорость фильтрации замедляется. В работе показано, что темпы замедления определяются кратностью корня блокирующего коэффициента фильтрации (9).
При n ≥ 1 замедление скорости фильтрации происходит настолько резко, что процесс фильтрации длится неограниченно долго. Чем меньше вакантных малых пор остается в пористой среде, тем сложнее частице заблокировать свободную пору, поскольку основной поток суспензии движется через поры больших размеров.
При 0 < n < 1 скорость фильтрации также уменьшается с ростом осадка, но в меньшей степени. В этом случае осадок достигает максимального значения за конечное время. В момент времени t = tmax все малые поры блокированы осажденными частицами. Процесс фильтрации прекращается, и все взвешенные частицы суспензии свободно проходят через поры больших размеров от входа к выходу пористой среды.



