К задачам о найме сезонных рабочих относятся задачи, в которых предприятию в разное время требуется разное количество рабочей силы. Поэтому управляющее лицо должно выработать некоторую стратегию по найму и увольнению. Описание такой задачи встречается в работе [1, с. 424–425]. Название «сезонные рабочие» является несколько условным, оно связано с тем, что наиболее типична такая ситуация при выполнении каких-то работ, связанных с сезонностью, хотя, безусловно, та же методика может применяться и для решения задач, в которых потребность в рабочих меняется по иным причинам. На каждом промежутке времени необходимо осуществить выбор между возможными вариантами: либо содержать ровно столько рабочей силы, сколько требуется на этот период, а затем увольнять лишних или нанимать недостающих, либо содержать лишнюю рабочую силу, которая не нужна в настоящий момент, но может пригодиться в последующем. И тот и другой способы действия сопряжёны с расходами. Содержание лишней рабочей силы приводит к дополнительным расходам на зарплату, которая выплачивается «ненужным» рабочим. Процедура поиска новых сотрудников также требует средств (необходимо дать объявление, что требуются сотрудники, содержать специалистов, которые будут проводить отбор подходящих сотрудников, обучать новых людей и т.д.). В некоторых случаях нужно учесть и расходы по увольнению (например, выплаты тех или иных компенсаций увольняемым) – такие расходы есть не всегда, но необходимо уточнить их наличие или отсутствие. Поэтому решение о том, какой вариант выбрать в каждой конкретной ситуации, необходимо принимать на основании знания точного количественного соотношения между расходами по найму-увольнению и расходами по содержанию излишка рабочей силы. Расходы по найму, которые в том или ином виде есть практически всегда, удобно разбить на две группы: индивидуальные (то есть зависящие от количества нанимаемых людей – расходы на каждого нанимаемого отдельно) и общие (не зависящие от количества нанимаемых людей). Так, расходы на объявление о том, что требуются рабочие, являются общими – цена такого объявления будет одинакова, вне зависимости от того, нанимаем мы троих человек или десятерых, а расходы на униформу или на оформление документов являются индивидуальными – эти расходы пропорциональны количеству нанимаемых людей. Удобно сразу зафиксировать эти расходы в виде двух сумм: суммарные общие расходы С (в расчете на период времени) и суммарные индивидуальные расходы k (в расчете на одного нанимаемого человека).
Задачу о найме сезонных рабочих можно в общем виде сформулировать следующим образом. Известно, что некоторой управляемой организации в n различных промежутков времени требуется различное минимально допустимое количество рабочей силы: а1, а2, … аn. Известна также стоимость процедуры найма дополнительных рабочих (общие расходы по найму составляют С единиц, а индивидуальные расходы по найму составляют k единиц за каждого рабочего). Также известны издержки v на содержание каждого лишнего рабочего в каждый промежуток времени и расходы u, связанные с увольнением каждого рабочего (если расходы по увольнению отсутствуют, то можно считать, что они равны 0). Требуется составить оптимальный план по найму и увольнению рабочих на весь рассматриваемый период времени, минимизирующий суммарные издержки.
В литературе рассматривается довольно громоздкое решение данной задачи [1, с. 425–426], основанное на составлении большого количества таблиц, значения в которых рассчитываются при помощи рекуррентного уравнения Беллмана [2, с. 216], понимание которого требует очень высокого уровня математической грамотности от менеджера. В работе [3] отмечается, что очень часто это создает совершенно ненужные трудности для специалистов экономистов и менеджеров, так как существуют более простые методики решения подобных задач. В указанной выше работе [3] решение задач динамического программирования осуществляется также с помощью таблиц. В ряде работ (см., например, [4, 5]) в разделе «динамическое программирование» рассматриваются задачи о нахождении кратчайшего маршрута, расчеты в которых осуществляются на графах. В настоящее время задача о нахождении кратчайшего маршрута эффективно решается с помощью навигаторов и поэтому представляет мало практической ценности. В то же время метод нахождения решений с помощью графа, благодаря своей наглядности и простоте, может, на наш взгляд, быть эффективно использован при решении ряда практических задач экономики и управления. В задаче о нахождении кратчайшего маршрута граф задан по условию – это схема дорог, но в задаче о найме сезонных рабочих изначального никакого графа нет. В настоящей работе показана возможность решения с помощью графов задачи о найме сезонных рабочих. Описано, каким образом условия данной практической задачи можно представить с помощью графа, представлен алгоритм составления графа, а также сам метод решения задачи. Этот новый подход к решению задачи о найме является более кратким, позволяет провести дополнительный финансовый анализ ситуации и найти не только наилучшее решение, но и возможные его вариации, что позволяет легко корректировать найденный результат в изменяющихся условиях.
Предварительно разберем предлагаемую нами методику принятия решения о найме на конкретном примере. Пусть предприятию требуется: на май – 10 человек, на июнь – 12, на июль – 14, на август – 11, на сентябрь – 10, на октябрь – 12. Требуется составить оптимальный план найма при условиях, что:
1) общие расходы по найму составляют 50 тысяч рублей (тыс. руб.) в месяц;
2) индивидуальные расходы по найму составляют 5 тыс. руб. на каждого нового рабочего;
3) в случае, если нанятый рабочий не выполняет работы, ему выплачивается минимальная заработная плата 10 тыс. руб.;
4) обязательная компенсация при увольнении – 2 тыс. руб.
Решение: По данным задачи построим граф. На начальном этапе мы имеем 0 рабочих (изображаем вершину графа кругом, подписанным числом 0), на май необходимо минимум 10 рабочих, но мы можем нанять и больше, с запасом на июнь (12 человек) и июль (14 человек). Поэтому изобразим на графе круги 10, 12 и 14 (см. рис. 1, столбец «май»).
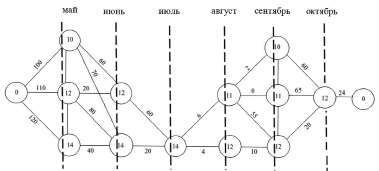
Рис. 1. Граф возможных вариантов найма сезонных рабочих по месяцам. Внутри кругов указано количество рабочих, а на линиях – расходы по соответствующим действиям
На июнь месяц требуется 12 рабочих, поэтому возможно иметь в этом месяце либо 12, либо 14 рабочих (меньшее количество, чем 12, недопустимо по условию задачи; большее количество, чем 14, нигде далее не требуется), изображаем возможные состояния двумя кругами. В июле требуется 14 рабочих, больше не требуется нигде, поэтому это будет единственным возможным состоянием. Аналогично, в августе можно держать либо 11, либо 12 рабочих (большего количества на дальнейших этапах уже не понадобится). В сентябре возможно иметь 10, 11 или 12 рабочих. И наконец, на последнем этапе, в октябре, единственным разумным вариантом будет иметь 12 рабочих. Далее все рабочие увольняются. Все круги можно соединить линиями (ребра графа). Однако некоторые линии являются заведомо излишними (это варианты действий, которые мы заведомо предпринимать не будем). Например, на участке «май – июнь» на рис. 1 вариант 14 в мае не соединен с вариантом 12 в июне, так как это соответствует найму 14 человек в мае и дальнейшему увольнению двух из них. Но совершенно ясно, что этот вариант заведомо бессмысленный. Зачем было нанимать четырёх лишних человек в мае? Мы их наняли с тем, что они понадобятся в июле. Если мы уволим двоих в июне, то получится, что они просто посидели в мае, не работая, получили зарплату и были уволены. Ясно, что такой вариант не выгоден. Однако, если кто-то соединит и эти два круга, то он не придет к ошибочному решению – он просто просчитает заведомо неразумный способ и отвергнет его как более дорогой. Тем не менее лишние линии загромождают чертеж и увеличивают время решения задачи, поэтому очевидно, невыгодные варианты лучше не соединять.
После построения графа переходим к расчетам затрат для каждого способа действия. Например, ребро «0–10» соответствует найму 10 рабочих в мае месяце. Соответствующие расходы составят 50 тыс. руб. общих расходов, а также 10×5 = 50 тыс. руб. индивидуальных расходов (нанимается 10 человек по 5 тыс. руб. за человека), итого потрачено 100 тыс. руб. (50 + 50 = 100). Записываем над соответствующим ребром графа число 100.
Если нанимать 12 рабочих, то наши затраты будут составлять уже 50 + 12×5 = 110 тыс. руб. – это вновь те же 50 тыс. руб. общих расходов плюс 12×5 = 60 тыс. руб. индивидуальных расходов. Аналогично, если нанимать 14 рабочих, то получим 50 + 14×5 = 120 тыс. руб. Переходим теперь к участку «май – июнь». Если в мае было нанято 10 рабочих, а затем в июне их будет 12, то это соответствует дополнительному найму двух человек. В результате опять потребуется осуществить общие расходы в 50 тыс. руб. (мы перешли к новому месяцу), плюс индивидуальные расходы составят 2×5 = 10 тыс. руб. Итого, записываем на ребре «10–12»: 50 + 10 = 60 тыс. руб. Аналогично, ребро «10–14» подписывается числом 70 = 50 + 5×4 (дополнительно нанимаются четверо рабочих). На участке «12 в мае – 12 в июне» мы никого не нанимаем и не увольняем, но в этом случае у нас было 2 лишних человека в мае, которым мы как раз в конце мая или начале июня должны выплатить зарплату в размере 2×10 = 20 тыс. руб. Это число и располагаем на графе (мы учитываем зарплату только неработавших сотрудников – зарплата работающим есть в любом случае и она будет одинакова во всех трех вариантах в мае месяце, включение ее в граф не изменит выбора решения, а только увеличит цифры и усложнит расчеты). Участок «12 в мае – 14 в июне» соответствует также содержанию двух лишних рабочих в мае (зарплата 20 тыс. руб.) + найму еще двух рабочих (60 тыс. руб.), поэтому данный отрезок подписывается числом 80. Участок «14 в мае – 14 в июне» не требует расходов по найму, но зарплата выплачивается уже четверым рабочим, откуда получаем число 40 (4×10). Расходы на участке «июнь – июль» подсчитываются аналогично (см. рис. 1). Расходы на линии «14 в июле – 11 в августе» соответствуют увольнению трех сотрудников. Поэтому нет расходов по найму, нет расходов на зарплату лишним рабочим, но необходимо выплатить компенсацию троим увольняемым, по 2 тыс. руб. каждому (2×3 = 6 тыс. руб.). Участок «14 в июле – 12 в августе» соответствует увольнению двоих (расход 4 тыс.руб.). Если бы при увольнении не было бы никакой компенсации, то на обоих участках стояли бы нули. Далее переходим к участку «август – сентябрь». Вариант «11 в августе – 10 в сентябре» соответствует увольнению одного человека, т.е. выплате компенсации в 2 тыс. руб., вариант «11–11» не требует никаких затрат, так как лишних в августе не было, вариант «11–12» требует найма одного человека, расходы на которого составят 50 + 5 = 55 тыс. руб. (общие + индивидуальные). Вариант «12–12» соответствует содержанию одного лишнего человека в августе, расходы равны его зарплате. Расходы «сентябрь – октябрь» подсчитываются аналогично: «10–12» соответствует найму двух человек (60 тыс. руб.), вариант «11–12» – найму одного человека (55 тыс. руб.) + содержание одного лишнего(10 тыс. руб.), что составляет 65 тыс. руб., вариант «12–12» – зарплата двум лишним – 20 тыс. руб. Наконец, в октябре увольняются все 12 рабочих, поэтому мы выплачиваем компенсацию в 12×2 = 24 тыс. руб.
Подсчитав все расходы, необходимые для найма сезонных рабочих, мы свели задачу к задаче о нахождении кратчайшего (в данном случае, самого дешевого) маршрута, если представить, что числа, стоящие между кругами – это расстояния между пунктами (или цены за соответствующие перевозки), решение такой задачи возможно осуществить сетевыми методами [5, с. 228; 6, c. 66]. Может она быть решена и методами динамического программирования [1, 4]. Вкратце суть решения сводится к следующему. Задача разбивается на этапы. В данном случае разбивка на этапы происходит естественным образом: каждый этап – это определённый месяц. На рисунке этапы выделены пунктирными линиями. Далее решение осуществляется от последнего этапа к первому. Для каждого «пункта», то есть круга, рассчитывается наименьшая стоимость пути до последнего круга (увольнение всех). Соответствующее число указывается рядом с кругом. Далее уже используется найденное число без повторного перебора всех возможных вариантов путей от данного круга. Так, для круга с числом 12 в октябре месяце мы поставим число 24 – стоимость увольнения всех. Выделяем путь стрелкой. Переходим к кругам в сентябре. Из каждого из них есть только один «путь» к октябрю, то есть к кругу 12. Стоимости рассчитываются суммированием числа стоящего на этом пути и числа стоящего рядом с кругом 12 в октябре (см. рис. 2). Так, рядом с кругом 10 ставим число 84 = 60 + 24, рядом с кругом 11 записываем 89 = 65 + 24, рядом с кругом 12 ставим 44 (20 + 24). Все пути выделяем стрелками (заметим, что сравнивать их между собой не надо, это единственно возможные варианты маршрутов из данных кругов, а в расчете должны быть охвачены все круги). В августе из круга 11 есть уже три возможных пути. Сравним их и выберем наилучший. Если пойти по пути «11–10», то есть уволить одного, то итоговые затраты составят 2 тыс. руб. в текущем месяце и 84 потом (число 84 видим рядом с кругом 11, а число 2 – на самом пути), то есть итоговые расходы составят 86 тыс. руб. Аналогично, путь «11–11» дает расход 0 + 89 = 89, а путь «11–12» дает итоговый расход 55 + 44 = 99. То есть самым выгодным оказывается «верхний» путь «11–10» со стоимостью 86. Выделяем его стрелкой. Для круга 12 есть только один путь «12–12» со стоимостью 10+44=54. Все круги августа подсчитаны, переходим к июлю. Имеется только один круг 14, но из него есть два пути, которые необходимо сравнить. Верхний путь приведет к расходам 6 сейчас + 86 потом, то есть составит 92 тыс. руб. Нижний путь составит 4 + 54 = 58, что гораздо дешевле, поэтому выбираем его, выделяем стрелкой и подписываем рядом с кругом 14 число 58. Аналогичные расчеты проводим для всех кругов июня, затем мая и наконец для начального нулевого круга (показано на рис. 2). Итак, мы видим, что минимальные расходы по «найму – увольнению» составляют 238 тыс. руб. Двигаясь от нулевого круга по стрелкам, находим оптимальный план действий: нанять в мае 14 рабочих, оставить их в июне и июле, в августе уволить двоих и оставить 12 рабочих до октября (показано жирным на рис. 2).
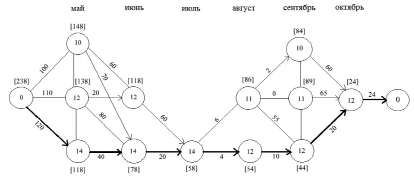
Рис. 2. Граф вариантов найма сезонных рабочих с расчетом соответствующих расходов. Оптимальный вариант выделен жирными стрелками. Оптимальные расходы показаны в квадратных скобках
Сформулируем теперь общий алгоритм решения задачи.
1. Разбиваем задачу на этапы (периоды, в которые минимальная потребность в рабочей силе постоянна). Выписываем эти этапы последовательно в одну строку.
2. Изображаем вершины графа – круги, обозначающие возможные состояния системы. Слева изображаем начальное состояние системы. Затем под названием каждого этапа перечисляем все допустимые варианты количества рабочих, которые могут быть в системе на данном этапе, начиная от минимального (заданного по условию задачи) и заканчивая максимальным количеством, которое может потребоваться в дальнейшем. Затем изображается конечное состояние, когда работа завершена и все рабочие уволены.
3. Соединяем ребрами графа все состояния каждого предыдущего этапа со всеми состояниями последующего этапа (переходы, которые не представляются разумными, можно опускать).
4. На каждом ребре указываем стоимость соответствующего перехода. Для этого отвечаем на следующие вопросы: были ли на предыдущем этапе лишние рабочие, которым нужно выплатить зарплату? Если да, то умножаем v на количество лишних рабочих. Требуется ли нанять или уволить новых людей и сколько? Если надо нанять, то вычисляем С + km (m – количество новых людей, которых необходимо нанять, оно рассчитывается как разность между количеством людей на следующем этапе и на предыдущем). Если требуется уволить рабочих, то количество увольняемых умножается на расход по увольнению u. Суммируем все расходы и подписываем их рядом с соответствующим ребром.
5. Считая, что числа на ребрах – это расстояния между пунктами-вершинами, находим кратчайший маршрут от начального до конечного состояния по известному алгоритму динамического программирования (cм. [1, c. 413]). Данный «маршрут» как раз и соответствует оптимальному плану найма, а его «длина» – минимальным расходам.
Замечание. В описанной ситуации деятельность организации прекращалась. Нередко приходится иметь дело с ситуацией, когда нет определенной точки, в которой бы ожидалось прекращение деятельности организации (бесконечный горизонт планирования [7, с. 253]). Деятельность продолжается на протяжении года, а на следующий год потребности в рабочей силе повторяются. Было бы ошибкой решать такую задачу просто в период с января по январь, а затем переносить результат на следующий год (в январе не происходит увольнения всех сотрудников). В этом случае находят точку, в которой будет требоваться максимальное количество людей – это количество будет соответствовать реально нанятому (больше нигде не требуется, нанимать меньше нельзя, так как будет недостаток в рабочей силе). Граф строится от начала работы до этой точки и далее от этой точки – полный рабочий год (например, если работа начинается с января, а максимальная потребность в рабочих имеется в июле, то граф строят от января первого года до июля второго года работы). Решения, принятые в участке от начала до максимума, применяются однократно, а на участке от максимума до следующего максимума циклически повторяются.



