Предложено множество математических и физических моделей глаза человека от относительно простых до более глубоко проработанных [1]. В настоящей статье предлагается вариант комбинированной математической модели глаза человека с параметрами, изменяемыми в зависимости от расстояния до объекта наблюдения.
Среди моделей глаз наиболее распространённым и проработанным является вариант, предложенный Лиоу и Бреннаном [2]. Известные аналоги обладают существенным недостатком, связанным с отсутствием учета градиентного показателя преломления хрусталика глаза. Работы, направленные на улучшение существующих моделей глаза, проводятся до настоящего времени [3, 4], что подтверждает актуальность исследования. Следует отметить, что, кроме не обладающей достаточной точностью модели Наварро [2], отсутствуют модели, описывающие аккомодацию глаза во всем диапазоне: от бесконечности до «расстояния наилучшего зрения». Это затрудняет исследование и разработку объемных дисплеев, которая связана с экспертной оценкой качества формируемых изображений, с построением математической модели оптической системы «дисплей – человек».
Для этого, в частности, необходимо определение зависимости ряда определяющих характеристик глаза от расстояния до наблюдаемого объекта.
Постановка задачи исследования
Необходимо выявить зависимости базовых параметров глаза от расстояния до наблюдаемого объекта, т.е. при различных степенях его аккомодации. При этом используются вышеуказанные модели [1, 2]. Для решения поставленной задачи предлагается, руководствуясь принципом неизменности объема хрусталика при различных степенях его трансформации (как несжимаемого тела) в процессе аккомодации, построить базовые зависимости геометрических и оптических характеристик составляющих элементов глаза, чтобы иметь возможность получения достаточно четкого изображения на сетчатке глаза при его любом удалении от объекта наблюдения. Разработанную модель глаза планируется использовать для оценки качества формируемого изображения в оптической системе макета объемного дисплея, конструкция которого, по сравнению с ранее описанной моделью [5], существенно изменена (рис. 1).
Под объемным дисплеем в нашем контексте понимается устройство, формирующее изображение, воспринимаемое наблюдателем в качестве объемного, т.е. занимающего определенное физическое пространство. В настоящее время существует достаточно много подобных конструкций, однако они обладают рядом существенных недостатков. К ним относятся высокая стоимость, неудовлетворительное качество получаемого изображения, необходимость обработки больших объемов информации и т.п., которые препятствуют их широкому распространению. В рамках выполняемого авторами проекта по созданию трехмерного дисплея эти недостатки планируется устранить. При этом предполагается использование разработанной модели глаза, так как выходные каскады оптической системы дисплея создают мнимое увеличенное прямое изображение объекта, оценка качества которого без разработанной модели глаза представляется весьма затруднительной.
Результаты исследования и их обсуждение
Для получения рабочих выражений за основу принят принцип неизменности объема хрусталика глаза в любых его трансформациях, возникающих при адаптации глаз к условиям наблюдения. Хрусталик глаза можно представить в виде двух объединенных секторов пары пересекающихся шаров (рис. 2). Из известного выражения объема сектора шара, отсекаемого плоскостью, выразим объем сектора первого шара, имеющего в начале построения радиус R11 (рис. 2):
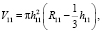 (1)
(1)
где R11 – начальный радиус задней поверхности хрусталика, а h11 и h21 – начальные стрелки секторов. Аналогично определяется объем второго сектора. При этом R21 – начальный радиус передней поверхности хрусталика, а h21 – начальная стрелка второго сектора. Сумма объемов этих секторов определяет начальный объем хрусталика.
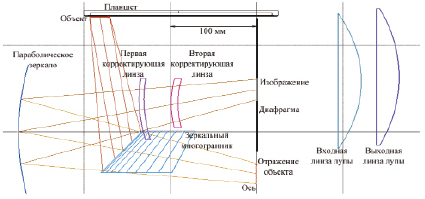
Рис. 1. Схема компоновки макета объемного дисплея (вид сбоку)
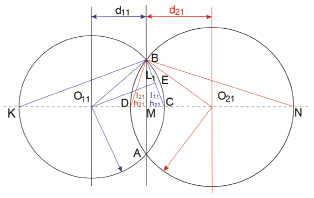
Рис. 2. Схема секторов, формирующих хрусталик глаза, где d11 и d21 – расстояние от центров окружности до центральной оси, A, B, C, D, E, K, L, M, N – вспомогательные точки при построении
При аккомодации на ближний объект радиусы обеих поверхностей хрусталика уменьшаются и изменяются стрелки секторов. Примем, что после аккомодации для первой сферы, отвечающей за заднюю поверхность хрусталика, радиус становится равным R12, а стрелка сектора – h12, для передней поверхности хрусталика радиус равен R22, а стрелка сектора соответственно h22.
Частичные объемы секторов хрусталика также изменяются, однако при этом их сумма остается постоянной. Введем обозначения объемов частей хрусталиков и приравняем их:
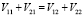 . (2)
. (2)
Из схемы на рис. 2 можно выделить другие связи между размерами хрусталика:
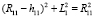 . (3)
. (3)
Откуда
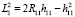 (4)
(4)
и, соответственно:
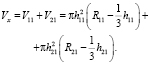 (5)
(5)
Далее описывается использование конкретных размеров неаккомодированного глаза в модели Лиоу – Бреннана.
Следует отметить, что хрусталик по модели Лиоу – Бреннана имеет асферические поверхности, которые создают избыточную сложность в точном воспроизведении объемов отдельных секторов хрусталика и его определяющих размеров. Для того, чтобы избежать этой сложности в работе, принято упрощение формы этих поверхностей и замена их шаровыми. Модификация формы поверхностей практически не изменяет глубину ее фокусировки, а влияет только на хроматические аберрации. В нашем случае модель глаза строилась для оценки четкости получаемого изображения, поэтому приближение сферичности поверхностей хрусталика является вполне приемлемым. При этом необходимо строгое выполнение условий точного совпадения поперечных размеров секторов в местах стыковки составных частей (секторов) модифицированного хрусталика (по краям и по центру), а также гладкой (без разрывов) «стыковки» коэффициентов преломления на границах этих секторов. Поэтому с использованием полученных выше выражений решалась задача построения математических моделей хрусталика и глаза с параметрами, адекватными базовой (не аккомодированной) модели Лиоу – Бреннана. Задача решалась методом последовательных приближений. Для этого вводились различные значения параметров и проверялась адекватность получающейся модели. При этом для проверки адекватности использовались значения характеристик базовой модели Лиоу – Бреннана, которая ориентирована на бесконечно удаленный объект (таблица).
Параметры оптической схемы глаза в модели Лиоу – Бреннана
|
№ по- верх- ности |
Описание |
Радиус кривиз- ны, мм |
Параметр кривизны |
Расстояние до следующей поверхности, мм |
Показа- тель пре- ломления |
Коэффи- циент дисперсии |
Полу- диаметр, мм |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
Передняя поверхность роговицы |
7,77 |
–0,18 |
0,55 |
1,376 |
50,23 |
5 |
|
2 |
Задняя поверхность роговицы/Передняя поверхность водянистой влаги |
6,4 |
–0,6 |
3,16 |
1,336 |
50,23 |
5 |
|
3 |
Радужная оболочка со зрачком (находится в водянистой влаге) |
∞ |
0 |
0,0 |
1,336 |
50,23 |
1,25 |
|
4 |
Задняя поверхность водянистой влаги / Передняя поверхность хрусталика |
12,4 |
0 |
1,59 |
Коэффициенты полинома n0 = 1,368, nr2 = –0,002, nz1 = 0,050, nz2 = –0,015 |
5 |
|
|
5 |
Граница раздела составных частей хрусталика |
∞ |
0 |
2,43 |
Коэффициенты полинома n0 = 1,407, nr2 = –0,0020, nz2 = –0,0066, |
5 |
|
|
6 |
Задняя поверхность хрусталика / Передняя поверхность стекловидного тела |
–8,1 |
0,96 |
16,239 |
1,336 |
50,23 |
5 |
|
7 |
Задняя поверхность стекловидного тела/ Сетчатка |
–12 |
0 |
5 |
|||
В результате получена модифицированная математическая модель глаза (рис. 3), входным параметром которой является расстояние от объекта наблюдения до роговицы глаза d (мм). Используем расчетный адаптированный объем хрусталика Vxpm = 74,99. Далее, радиус входной части хрусталика Rlf = r3 задается в зависимости от степени аккомодации глаза. Диаметр хрусталика глаза 2L = d3 задается по аппроксимирующему выражению в зависимости от степени аккомодации глаза.
Стрелка входного сектора хрусталика:
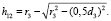 (6)
(6)
Стрелка выходного сектора хрусталика:
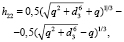 (7)
(7)
где параметр q равен
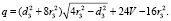 (8)
(8)
Остальные вычисляемые значения параметров глаза или константы определяются согласно нижеприведенным зависимостям и данным:
радиус кривизны входной границы роговицы: Rc = Const = 7,77;
толщина роговицы: Tc = Const = 0,55;
радиус кривизны выходной границы роговицы: Ra = Const = 6,4;
расстояние от задней поверхности роговицы до зрачка: 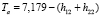 ;
;
кривизна зрачка Rp = Const = Infinity и толщина зрачка: Tp = Const = 0;
радиус входной части хрусталика Rlf = r3, как указано выше, задается согласно аппроксимирующему выражению: r3 = 10,2 – 1,75 ln (A + 1);
толщина входного сектора хрусталика: 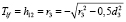 ;
;
радиус кривизны границы смыкания двух частей хрусталика: Rlb = Const = Infinity; расстояние от границы раздела до задней поверхности хрусталика:
радиус задней поверхности хрусталика: 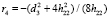 ;
;
продольный размер стекловидного тела: Tv = Const = 16,239;
радиус сетчатки глаза: Rr = Const = –12.
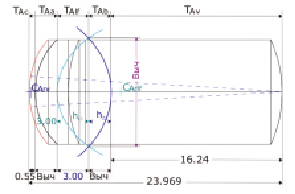
Рис. 3. Схема модели глаза с обозначениями
Рассмотрим зависимость параметров предложенной модели глаза от расстояния до объекта наблюдения. Для этого воспользуемся формой записи аналогичных характеристик из аппроксимационной модели Наварро:
радиус линзы хрусталика:
r3 = 10,2 – 1,75 ln (A + 1);
радиус первой поверхности стекловидного тела:
r4 = –6 + 0,2294 ln (A + 1);
диаметр входной камеры:
d2 = 3,05 – 0,05 ln (A + 1);
диаметр линзы хрусталика:
d3 = 4 + 0,1 ln (A + 1);
коэффициент преломления хрусталика:
n3 = 1,42 + 9 10e-5 (10 A + A);
асферичность хрусталика:
k3 = –3,132 – 0,34 ln (A + 1);
асферичность передней поверхности стекловидного тела:
k4 = –1 – 0,125 ln (A + 1),
где А – аккомодация в системе единиц СИ: A = 1000/d (d – расстояние до объекта, мм). При удалении объекта на бесконечное расстояние аккомодация равна A = 0. Следовательно, все правые части аппроксимаций (за исключением постоянных коэффициентов) равны нулю, что представляет возможность использовать полученную ранее модифицированную модель полностью расслабленного глаза как одну из образующих точек реализуемой аппроксимации.
В результате получим конечную формулу для радиуса передней поверхности хрусталика: r3 = 12,4 – 2,669 ln (A + 1) на основе вычисленных значений для полностью аккомодированного глаза и их аппроксимации.
Градиентный коэффициент радиального преломления (ГКРП) определялся методом последовательных приближений, поэтому следующим шагом является аппроксимация полученных значений. С использованием таблиц данных и регрессионного анализа для ГКРП получается следующее аппроксимирующее выражение:
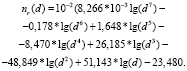 (9)
(9)
На основе полученных зависимостей для дальнейшей автоматизации расчетов в пакете Matlab написана программа, позволяющая определить значения параметров модели глаза как функцию его расстояния от объекта наблюдения.
Для примера на рис. 4 представлен один из графиков расчетных характеристик основных элементов глаза.
Заключение
Построена математическая модель глаза, которая позволяет рассчитывать параметры его элементов в зависимости от расстояния до наблюдаемого объекта. Пример значений вычисленных характеристик для модели параметров модели глаза (расстояние до объекта d = 400 мм) приводится ниже:
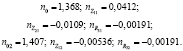 (10)
(10)
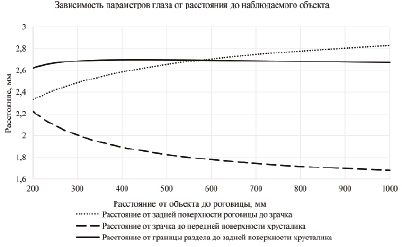
Рис. 4. График зависимостей расстояния между поверхностями глаза от расстояния до объекта наблюдения
По расчетным характеристикам построена модель в программе Zemax (рис. 5).
Рис. 5. Симуляция изображения на сетчатке и модель глаза в программе Zemax
Таким образом, сформулированная в работе задача, связанная с определением зависимости базовых параметров глаза от расстояния до наблюдаемого объекта (при различных степенях аккомодации хрусталика глаза), достигнута.
Полученная модель полезна при оценке характеристик получаемого изображения при оптическом проектировании, а также в офтальмологии для анализа и подбора персональных оптических устройств.
Работа выполнена при поддержке гранта № 1995ГС1/26878 Фонда содействия инновациям.



