Поиск информации в полнотекстовых базах данных – актуальное направление исследований. Рост количества электронных документов коррелируется с ростом возможностей компьютеров по хранению больших объемов информации и скорости ее обработки. Создаются полнотекстовые базы, включающие миллионы страниц тематических материалов. На персональных компьютерах и серверах накапливают электронные архивы эквивалентные десяткам тысяч томов, поиск в них проводится за 1–2 сек. [1]. Как правило, эффективный поиск выполняется в два этапа [1, 2]: предварительный поиск и отбор информации в тематические базы данных, затем поиск нужной информации конечным пользователем в сетевых или локальных полнотекстовых базах. Различаются следующие разновидности поиска в текстовом массиве [1]. Контекстный поиск – весь текст последовательно просматривается программой, слова сравниваются с запросом, выполняются логические операции и дополнительные условия поиска. Такой поиск прост, однако он медленный. Подокументно контекстный поиск – предварительно создается индекс, в котором есть списки слов каждого документа. По индексу определяются документы, содержащие слова запроса, для уточнения программа производит контекстный поиск в найденных документах. Индексный поиск [3–5] по всему содержанию документов – включает полную информацию обо всех словах текстов базы данных, включая их взаимное расположение. Содержание запроса сравнивается с полным полем информации в базе данных, при этом ищутся не документы, а требуемая информация. По найденным фрагментам текста выдаются тексты самих документов. Скорость такого поиска измеряется десятками гигабайт в секунду. Наиболее развитые технологии поиска обеспечиваются полнотекстовыми системами, при этом они опираются на модели поиска. Модель понимается как сочетание способов создания представлений документов, представлений поисковых запросов, критерия релевантности. К числу простейших относят модели дескрипторных информационно-поисковых систем, систем, использующих Дублинское ядро, а также модели, основанные на классификаторах. В последнем случае документы представляются идентификаторами классов в иерархической структуре классификатора, к которым относится искомый документ. Запрос – идентификатор интересующего пользователя класса, критерий релевантности определяется как совпадение класса или подкласса документа с классом в представлении запроса. В моделях контекстного поиска документ представляется как совокупность всевозможных слов и словосочетаний, не считая стоп-слов (служебные слова, предлоги, союзы и т.п.). По всем встречающимся в документах словам и словосочетаниям, кроме стоп-слов, строится индекс, слова, выделенные из текста документа, приводятся к «каноническому виду» с помощью поддерживаемых в системе словарей и средств грамматического разбора. Запрос подвергается грамматическому разбору, в процессе которого выделяются встречающиеся в его тексте слова и словосочетания. Документ считается релевантным, если какие-либо слова или словосочетания из запроса в тексте документа встречаются с точностью до грамматических форм. Более жесткий критерий релевантности – вхождение в текст документа всех названных в запросе слов и словосочетаний [6].
Предлагаемые ниже способы идентификации множества слов соотносятся с моделью контекстного поиска. Способ ориентирован на ускорение идентификации в исследуемом документе слов запроса. В качестве алгоритмической основы ускорения рассматривается разрядное распараллеливание операций сравнения и идентификации множества слов строкового типа. Метод строится по аналогии с поразрядно-параллельным алгебраическим сложением чисел без вычисления переноса, описание оригинала заимствуется из [8].
Сравнение двоичных чисел. Предполагается, что сравниваемые числа имеют формат целочисленных двоичных полиномов с нумерацией разрядов справа налево:
, 
, 
, 
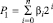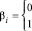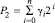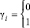, (1)
Пусть число А принято в качестве уменьшаемого, B – за вычитаемое. В этом случае B записывается в обратном коде (единицы заменяются нулями, нули – единицами), затем используется тождественное преобразование:
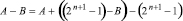, (2)
с учетом
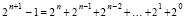, (3)
или, в позиционной системе,
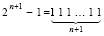. (4)
Над числом A и числом B, взятым в обратном коде, параллельно по всем номерам разрядов выполняется операция вертикального суммирования бит одного веса, затем A и B (в обратном коде) суммируются по схеме [7, 8], излагаемой ниже в примере 1. Согласно (2)–(4) для правильного результата от полученной суммы в виде однорядного знакоразрядного двоичного кода следует вычесть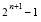 
. Это равносильно тому, что с полученным результатом складывается 
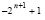– к младшему разряду добавляется + 1, а к разряду веса 
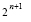добавляется – 1. Результат сравнения определяется знаком старшего ненулевого разряда в окончательном однорядном коде. Если знак этого разряда отрицательный, то A < B, если положительный, то A > B, если все разряды нулевые, то A = B.
Пример 1. Сравниваются двоичные числа 0110101100000000 (уменьшаемое) и 0110010101110010 (вычитаемое). После перевода вычитаемого в обратный код алгебраическому сложению подлежат:
0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0
1 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1
Параллельно по всем номерам разрядов j выполняется операция вертикального суммирования (CBj) бит равного веса:
+ 0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0
1 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1
1 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1
0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0
Над двухрядной суммой выполняется преобразование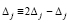 
, 
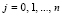, при этом –Δj заменяет значение j-го разряда в верхней разрядной сетке
(
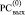), а 2Δj заменяет значение j + 1-го разряда (он всегда нулевой в результате CBj [7]) в нижней разрядной сетке (
):
|
+ |
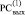- 1 |
- 1 |
- 1 |
- 1 |
0 |
0 |
0 |
- 1 |
- 1 |
0 |
0 |
0 |
- 1 |
-1 |
0 |
- 1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
Параллельное по всем разрядам суммирование по вертикали влечет
0 0 0 0 0 1 1 0 -1 0 0 1 0 -1 1 -1
Результат корректируется в соответствии с (2)–(4), что влечет окончательное значение алгебраической суммы
0 0 0 0 0 1 1 0 -1 0 0 1 0 -1 1 0
Старший ненулевой разряд положителен, следовательно, первое число больше второго.
Разрядное распараллеливание сравнения строк. Изложенный способ переносится [9] на сравнение элементов строкового типа, для краткости – строк. Все символы представляются в ASCII-коде в двоичной форме. Набор двоичных кодов всех символов строки в порядке расположения интерпретируется как единое числовое значение. Сравнение полученных двоичных кодов выполняется путем алгебраического сложения изложенным поразрядно-параллельным способом, но при этом в соответствии с лексикографическим упорядочением слов выравнивание весов разрядов выполняется по старшим разрядам, недостающие младшие разряды дополняются нулями.
Пример 2. Сравниваются слова 'poisk' и 'primer'. Их двоичный код с выравниванием старших разрядов соответственно примет вид
0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 1 1 1 0 0 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 1 0 1 0 1 1 0 0 1 0 1 0 1 1 1 0 0 1 0
Слово «poisk» интерпретируется как уменьшаемое, «primer» – как вычитаемое. После перевода вычитаемого в обратный код алгебраическому сложению подлежат
0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0
1 0 0 0 1 1 1 1 1 0 0 0 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1
Параллельно по всем номерам разрядов выполняется операция CBj:
+ 0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0
1 0 0 0 1 1 1 1 1 0 0 0 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1
0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1
0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0
Выполняется преобразование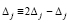 
, 
, –
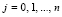+ 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 0 0 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 0 0 0 -1 -1 -1 -1 -1 0 0 0 -1 -1 0 0 0 -1 -1 0 -1
1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 0 1 1 1 0 0 0 1 1 0 1 0
Параллельное по всем разрядам суммирование по вертикали влечет
1 0 0 0 0 0 0 0 0 0 0 -1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 -1 0 0 1 0 -1 1 -1
Результат корректируется в соответствии с (2)–(4), что влечет
0 0 0 0 0 0 0 0 0 0 0 -1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 -1 0 0 1 0 -1 1 0
Старший ненулевой разряд отрицателен, следовательно, первое слово лексикографически меньше второго: 'poisk' < 'primer'. Численное и программное моделирование способа представлено в [10]. Изложенное сравнение инвариантно относительно числа разрядов и без учета временной сложности идентификации старшего ненулевого разряда занимает время одной бинарной операции над двоичными коэффициентами: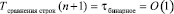 
, где n + 1 – число разрядов двоичного представления строки. Поразрядно-параллельное выделение старшего ненулевого разряда в знакоразрядном коде – самостоятельная схемотехническая задача. Искомый разряд можно выделить программно или аппаратно, в частности, на основе схем, представленных в [10]. Одна из таких схем требуется для дальнейшего использования и представлена непосредственно ниже.
Идентификация знака старшего ненулевого разряда может осуществляться на основе схемы сдваивания [10] по приводимому непосредственно ниже алгоритму.
Алгоритм 1.
Шаг 1. Если старший разряд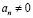 
, то по его значению идентифицируется результат сравнения и выполняется переход на шаг 4, иначе положить 
, 
, 
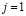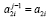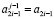и перейти на шаг 2.
Шаг 2. По схеме сдваивания на вход узла текущего уровня поступают значения разрядов. Для каждой пары с номером i (нумерация от нуля справа налево) происходит передача значения на следующий уровень по правилу:
2.1. Если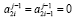 
, на уровень с номером j передается значение 0.
2.2. Если один из элементов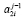 
или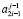 
имеет нулевое значение, а другой элемент – ненулевое значение, то на уровень с номером j передается значение ненулевого элемента.
2.3. Если элементы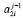 
и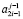 
имеют ненулевое значение, то на уровень с номером j передается значение старшего по номеру разряда в паре ненулевого элемента 
.
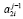Перейти на шаг 3.
Шаг 3. Если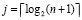 
, то выполнить переход на шаг 4. Иначе положить 
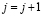и выполнить переход на шаг 2.
Шаг 4. Конец. Алгоритм заканчивает работу по условию: крайняя слева ветвь при сдваивании встречает в узле ненулевое значение, или, на шаге с номером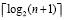 
,
в узле этой ветви оказывается разряд с нулевым значением.
Отслеживание знака старшего ненулевого разряда выполняется по шагам пути значения (n + 1)-го разряда в схеме сдваивания до первого уровня с ненулевым значением узла, которое и явится идентификатором знака. Если ненулевое значение не появилось, то на шаге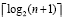 
алгоритм останавливает свою работу, идентифицируя совпадение слов (равенство двоичных кодов). Временная сложность алгоритма:
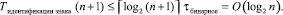
Алгоритм 1 используется в дальнейшем с незначительными изменениями.
Поразрядно-параллельная идентификация совпадающих фрагментов строк. Главная особенность способа состоит в том, что выполняется только один – первый – шаг поразрядно-параллельного вертикального сложения двоичных кодов двух сравниваемых строк [8]. Именно параллельно по всем номерам разрядов j выполняется операция CBj суммирования бит равного веса,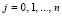 
. Все совпадающие по номерам разрядов биты в результате одного такого шага дадут в выходной верхней разрядной сетке 
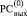нули [10]. Нижняя выходная разрядная сетка 
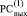для дальнейшего использования практически не понадобится. Выравнивание старших разрядов в примерах условно, поскольку ищется совпадение подмножества бит, вообще говоря, не обязательно в случае одинаковой по весам нумерации разрядов сравниваемых слов.
Пример 3. Идентифицировать все совпадающие части двоичных слов 110000011110010111100011и 110010111110010111110001. Единственный шаг параллельного по всем разрядам выполнения CBj влечет
+ 1 1 0 0 0 0 0 1 1 1 1 0 0 1 0 1 1 1 1 0 0 0 1 1
1 1 0 0 1 0 1 1 1 1 1 0 0 1 0 1 1 1 1 1 0 0 0 1
0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0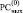 
1 1 0 0 0 0 0 1 1 1 1 0 0 1 0 1 1 1 1 0 0 0 0 1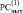 
Группы подряд идущих нулей в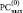 
в точности идентифицируют все совпавшие части двоичных кодов:
Идентификация совпадающих частей формализуется следующим алгоритмом.
Алгоритм 2.
Шаг 1. Слева от старшего разряда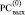 
формально полагается еще один единичный разряд для правильного начала алгоритма справа от единицы. Перейти на шаг 2.
Шаг 2. За границей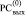 
справа формально дописывается еще один единичный разряд для правильного окончания алгоритма. Перейти на шаг 3.
Шаг 3. Идентификация каждой группы начинается с первого слева направо нуля, после ненулевого бита. При этом идентификация первого справа налево от цепочки нулей единичного бита выполняется по алгоритму 1 при условии его начала с первого слева направо нуля цепочки. Перейти на шаг 4.
Шаг 4. Если идентифицирован первый сверху вниз единичный разряд на шаге схемы сдваивания, то идентификация совпадающих частей завершена (единица в идентифицированное совпадение не входит), иначе перейти на шаг 3.
Число нулей идентифицированной группы равно числу бит двоичного представления совпавших фрагментов. Это число, равно как и местоположение идентифицированных промежуточных нулей, определяется номерами начального и конечного единичного разрядов в схеме сдваивания, выполняемой по алгоритму 1 при его вложении в алгоритм 2 [10].
Анализ выполняется параллельно по всем группам подряд идущих нулей. При этом в каждой группе он выполняется по алгоритму 2 от соответственного анализируемой группе первого слева направо нулевого разряда вдоль пути, который проходит значение первого слева направо после цепочки нулей ненулевого значения по схеме сдваивания сверху вниз к окончанию двоичного дерева. С целью максимального параллелизма от отмеченного первого слева направо нулевого разряда каждая группа включает в дерево все подряд младшие разряды двоичного представления слов до последнего слева направо включительно. Алгоритм останавливает работу на том шаге вдоль пути первого слева направо нуля, где после него первый раз встретилось ненулевое значение.
Нетрудно подсчитать, что временная сложность данного алгоритма в максимально параллельной форме составит
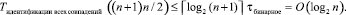
Такая схема довольно громоздка, ниже излагаются варианты сокращения количества сдваиваемых элементов.
Минимизированная по числу схемных компонентов идентификация совпадающих фрагментов строк получится, если каждая схема сдваивания будет начинаться, как на шаге 3 алгоритма 2, но при этом не будет включать все подряд младшие разряды сравниваемых слов, а только подряд идущие нулевые – с первой после них единицей.
Пример 4. Идентифицировать все совпадающие части в словах 'Лес' и 'Бег'.
Двоичный код сравниваемых слов с выравниванием старших разрядов соответственно примет вид
1 1 0 0 0 0 0 1 1 1 1 0 0 1 0 1 1 1 1 0 0 0 1 1
1 1 0 0 1 0 1 1 1 1 1 0 0 1 0 1 1 1 1 1 0 0 0 1
Поразрядно-параллельное сложение влечет
+ 1 1 0 0 0 0 0 1 1 1 1 0 0 1 0 1 1 1 1 0 0 0 1 1
1 1 0 0 1 0 1 1 1 1 1 0 0 1 0 1 1 1 1 1 0 0 0 1
0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0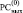 
1 1 0 0 0 0 0 1 1 1 1 0 0 1 0 1 1 1 1 0 0 0 0 1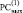 
Предложенный способ поясняется на рисунке.
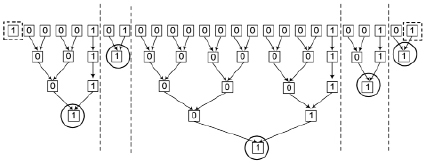
Пример идентификации групп подряд идущих нулей в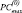 
Проблема будет заключаться в том, как правильно указать расположение всех сдваиваемых элементов для начального шага схемы сдваивания. Если это делать последовательно слева направо вдоль цепочки подряд идущих нулей, то утратится эффект максимального распараллеливания. Номер первого слева направо нуля в цепочке всегда известен по номеру включающего его разряда. В алгоритме 1 это был n-й разряд при отсчете от нуля, содержащий an. Местоположение заключительного нуля цепочки не требовалось. Теперь требуется знать такой номер для каждой цепочки нулей. Тогда по разности начального и конечного номеров нулей цепочки можно будет указать точное число сдваиваемых элементов на первом шаге схемы сдваивания, не прибегая к их последовательному построению. Требуемую идентификацию номеров можно выполнить следующим образом. Начальный слева направо номер разряда для цепочки нулей определяет сочетание подряд слева направо расположенной пары значений 1,0. Конечный слева направо номер разряда для этой же цепочки нулей определяет сочетание пары бит в обратном порядке: 0,1. Пусть сопоставленные процессорные элементы выдают номера разрядов каждого нуля при условии сочетания соседних бит 1,0, и пусть, аналогично, выдаются номера разряда каждой единицы при условии сочетания соседних бит 0,1. Пусть эти номера выдаются с соответственным каждому номеру идентификатором 1,0 или 0,1. Тогда они будут попарно обращены друг к другу как пара квадратных скобок, если потребовать, чтобы никакие другие процессорные элементы не выдавали каких-либо номеров, не удовлетворяющих данным условиям. Теперь достаточно попарно взять разность обращенных друг к другу соседних номеров, чтобы получить точное значение числа сдваиваемых элементов на первом шаге схемы сдваивания. Формально, чтобы каждая из таких схем обрабатывалась по алгоритму 1, достаточно в нем n заменить на значение разности начального и конечного номера цепочки нулей, а остальные номера элементов цепочки заменить на их разность с конечным номером. Так, например, для наибольшей схемы сдваивания на рисунке получатся модифицированные номера разрядов слева направо: 12, 11, 10, … , 2, 1, 0. Это даст 6 пар сдваиваемых слева направо нулей и не вошедшую в пару единицу (она получила нулевой номер). Все такие схемы сдваивания строятся и выполняются параллельно. В результате число схемных компонентов сокращается до количества разрядов слова, и временная сложность идентификации всех совпадающих частей составит
.
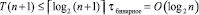Замечание 1. При таком способе надобность собственно в схеме сдваивания, строго говоря, отпадает: пары соседних обращенных друг к другу номеров уже идентифицируют заключенную между ними цепочку нулей, а разность между этими номерами идентифицирует количество нулей цепочки, т.е. совпавшие компоненты слов и количество элементов совпадения.
Замечание 2. Требует оговорки способ обмена между процессорными элементами, идентифицирующими пары соседних номеров, обращенных друг к другу. Это, однако, зависит от архитектуры параллельной вычислительной системы, от которой в целом абстрагировалось изложение данного метода.
Необходимо отметить, что при поиске всех совпадений, без выравнивания старших разрядов, пришлось бы выполнять взаимный сдвиг слов на один, два разряда и т.д. Правда все взаимно сдвинутые пары слов можно проверить на совпадение параллельно, что вновь увеличит число схемных компонент до значения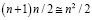 
. Без учета обмена, ввиду отсутствия схемы сдваивания, временная сложность последней модификации составит 
.
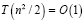Замечание 3. Все разряды в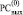 
, помимо нулевых цепочек, представляют собой цепочки единиц, что означает идентификацию всех несовпадающих фрагментов слов.
Возможные области применения. Предложенные схемы позволяют выполнить поразрядно-параллельный поиск в строке одновременно по нескольким маскам, параллельно идентифицировать полное и частичное совпадение с одной или несколькими масками поиска с единичной временной сложностью. Схемы распространяются на выявление совпадающих частей любой информации в двоичном коде, включая числовую. Без принципиальных изменений схемы переносятся на параллельную идентификацию значений условных выражений. С применением максимально параллельной сортировки схемы применимы для ускорения операций поиска, вставки, замены в двоичных и декартовых деревьях структур баз данных. Кроме того, схемы могут быть применены к идентификации бинарных двоично закодированных изображений или их фрагментов. Для этого достаточно матрицу изображения перевести в одномерный массив. Аналогично, могут идентифицироваться графы в матричном представлении. Схемы позволяют идентифицировать участки несовпадения (совпадения) с эталоном, что целесообразно при идентификации биометрических данных.
Заключение
Изложен метод разрядного распараллеливания элементарных операций информационного поиска. Метод основан на бинарном алгебраическом сложении двоичных полиномов без вычислений переноса. Представлено видоизменение метода для параллельной идентификации совпадающих фрагментов строк с логарифмической и единичной временной сложностью. Одно из возможных применений заключается в ускорении операций поиска, вставки, замены в двоичных и декартовых деревьях структур баз данных. Возможно применение для идентификации бинарных изображений и их фрагментов.