В современном мире алгоритмы оптимизации получают всё большее распространение, что вызвано усложнением задач и постоянной ограниченностью материальных и интеллектуальных ресурсов. Новые глобальные проблемы человечества приводят к усложнению задач, которое наблюдается во многих сферах, среди которых экология, производство, экономика, предсказание стихийных бедствий, безопасность граждан и многие другие. Конечность ресурсов диктует своим правилом необходимость оптимизации – получение лучшего результата при минимальных затратах. Поскольку оптимизация выражается поиском экстремумов математических функций, для неё изначально были созданы алгоритмы, именуемые сейчас детерминированными. Среди них такие алгоритмы, как метод Фибоначчи, метод обобщённого приведённого градиента, симплекс-метод и другие [1]. Однако в последние годы проблемы, задачи и модели обретают такие масштабы, что классических подходов оказывается недостаточно. И им на смену приходят методы, относящиеся к классу эвристических и стохастических. Они появились ещё в прошлом веке и на данном этапе своего развития представлены такими небезызвестными алгоритмами, как генетические, иммунные, роевые и другие. Такие алгоритмы часто имитируют поведение биологических систем для решения математических задач [2].
Целью данного исследования является изучение комбинации детерминированных и стохастических алгоритмов для компенсации их недостатков и оптимального использования преимуществ каждого из этих классов.
Так, детерминированные методы оптимизируют переданные им целевые функции посредством заранее определённой комбинации формул. Такие алгоритмы точны, но зачастую легко сваливаются в локальные экстремумы, не имея возможности из них выбраться. Кроме того, время работы таких методов экспоненциально возрастает при росте размерности задачи. В результате на достаточно больших задачах применение детерминированных алгоритмов зачастую оказывается нецелесообразным, если не невозможным.
Ввиду описанных недостатков стохастические методы антагонистичны детерминированным. Они не используют сложных математических вычислений, не пытаются аргументировать и объяснить свои решения, основаны на вероятностях и не гарантируют нахождения точного решения. Благодаря обширному вероятностному подходу такие методы проще выбираются из локальных экстремумов, имея больше возможностей по достижению глобальных.
В действительности, есть целый ряд задач, для которых ни один из предложенных классов алгоритмов не является панацеей. Детерминированные методы точны, но сваливаются в локальные максимумы и минимумы. Эвристические – могут определить глобальный экстремум, но находят лишь приближённые решения. Однако многие современные задачи настолько сложны и многомерны, что использование для их решения строгих математических алгоритмов становится невозможным. Проблематика таких задач постоянно изучается и расширяется [3].
С подобными задачами работают многие современные теории и науки. Среди них теория искусственного интеллекта во всех её аспектах и проявлениях, теория оптимизации и принятия решений, построения автоматизированных систем, управления ресурсами, логистики и другие. Данное исследование приводит упрощённый и понятный пример подобной задачи и описывает, как комбинация обоих классов алгоритмов позволяет сделать поиск оптимального решения и глобальным, и точным одновременно.
Так, в качестве детерминированного алгоритма был выбран метод обобщённого приведённого градиента из состава надстройки «Поиск решений» пакета Microsoft Excel [4]. Этот метод хорошо подходит для решения с нелинейными функциями-ограничениями, однако обладает всеми описанными выше недостатками детерминированных алгоритмов.
Эвристическим алгоритмом стала собственно разработанная иммунная система, написанная на языке C#. Относясь к классу эвристических стохастических алгоритмов оптимизации, искусственные иммунные системы имитируют поведение естественных иммунных систем живых организмов, оперируя так называемыми иммунными клетками, направленными на уничтожение проникших в организм антигенов путём генерации подходящих антител. Такие алгоритмы отлично распараллеливаются и хорошо подходят для исследования обширных пространств решений с большим количеством локальных экстремумов. Благодаря своей стохастичности иммунные алгоритмы (равно как и, например, генетические) в ряде случаев способны найти решение за гораздо меньшие промежутки времени по сравнению с детерминированными алгоритмами. Искусственные иммунные системы оперируют теми же понятиями, что и естественные, используя генерацию иммунных клеток, их приспосабливаемость и мутацию [5].
Постановка задачи
Как правило, эвристические алгоритмы наиболее рационально использовать на задачах очень большой размерности – несколько десятков, а то и сотен переменных. Именно в таких условиях применение детерминированных классических методов оказывается невозможным из-за экспоненциально возрастающего времени поиска решения. Однако в качестве тестового стенда была выбрана не слишком сложная функция Растригина в пятимерном пространстве и выглядящая следующим образом [6].
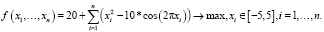
Такая функция обладает всеми необходимыми свойствами для того, чтобы её оптимизация классическими детерминированными алгоритмами была затруднительна. Однако благодаря ее простоте можно наглядно представить и её, и получаемое в ходе оптимизации решение. Графически такая функция в двухмерном пространстве выглядит так, как показано на рис. 1 [6].
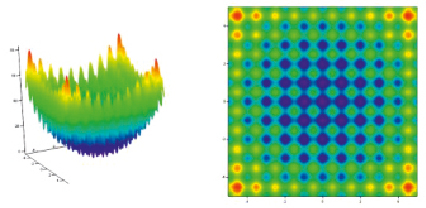
Рис. 1. Функция Растригина в двухмерном пространстве
Видим, что двухмерное представление этой функции имеет один глобальный минимум и четыре максимума, находящихся на концах спектра значений по обоим направлениям осей. Эти глобальные экстремумы находятся в тесном расположении с большим количеством локальных. В пятимерном пространстве минимум по-прежнему останется один, а вот количество максимумов значительно возрастёт пропорционально размерности пространства.
Методика решения
Для начала используем Microsoft Excel с целью поиска решения детерминированным методом обобщённого приведённого градиента (ОПГ). Нам известно, что максимумы будут находиться близко к границам всех осей, то есть их координаты близки к значениям –5 и 5. И это одно из допущений, используемых в рамках данного исследования, поскольку при решении реальных задач данных о расположении экстремумов зачастую не бывает. Таким образом, обычно неизвестен ни диапазон оптимальных значений xi, ни начальная точка, с которой лучше начинать искать. Мы же можем использовать в качестве точки старта поиска координату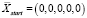 
. Составив задачу для надстройки «Поиск решений», получим следующее решение (рис. 2).
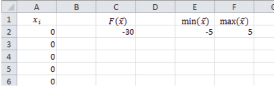
Рис. 2. Решение методом ОПГ
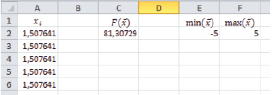
Рис. 3. Повторное решение методом ОПГ
Как видим, алгоритм ОПГ посчитал, что глобальный максимум находится в точке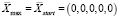 
. Продолжим анализ и возьмём новую стартовую точку 
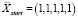. Результат будет другим (рис. 3).
В действительности, мы видим сваливание алгоритма ОПГ в локальный экстремум, характерное для детерминированных методов. Он находит максимум, ближайший к начальной точке, и видит, что за ним следует косинусоидальный спад значения, не замечая, при этом, что за спадом следует ещё более сильный подъём. При этом такой алгоритм обладает высокой точностью, которая нам необходима. Следовательно, теперь задача сводится к поиску приблизительного решения, которое затем можно будет подать на вход метода ОПГ для получения точного результата.Для достижения этой цели будем использовать созданный иммунный алгоритм.
После составления программного представления задачи и запуска алгоритма получим решение (рис. 4).
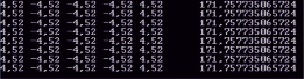
Рис. 4. Решение задачи иммунным алгоритмом
Такой полученный результат демонстрирует, что решение не улучшалось на протяжении некоторого количества итераций, что послужило для остановки процесса дальнейшей оптимизации – была достигнута так называемая точка останова иммунного алгоритма.
Так, согласно иммунному алгоритму, максимум описанной функции Растригина находится в точке
.
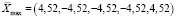При этом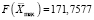 
.
Поскольку нам необходимо было найти приближённое решение, то точность была задана равной двум верным знакам после запятой. Кроме того, стоит пояснить некоторые параметры, которыми оперирует иммунный алгоритм и которые влияют на конечный результат. Так, многие эвристические алгоритмы работают над улучшением целевой функции посредством большого количества однородных программных объектов. В данном случае такими объектами являются иммунные клетки, аналогичные тем, которые призваны справляться с антигенами в биологических организмах. В рамках данной задачи количество таких клеток было равно 100. На каждом шаге алгоритма эти клетки обретали числовые значения и сортировались по убыванию. Следовательно, первыми в списке находились те клетки, приспособленность которых (значение целевой функции) была максимальной. Из этого поколения отбиралось 20 лучших клеток, для каждой из которых системой генерировалось по 20 клонов. Эти клоны мутировали, создавая вероятность получения ещё более качественных (приспособленных) клеток.
С учётом описанных выше параметров на решение задачи иммунному алгоритму понадобилось приблизительно 2 секунды. Изменяя же их, можно влиять и на скорость работы алгоритма. Однако в рамках данной задачи указанные значения параметров были приняты оптимальными.
Так, получив приблизительное решение, мы можем использовать его в качестве начального для дальнейшего уточнения при помощи алгоритма ОПГ. Подставив его в Microsoft Excel, получим следующий результат (рис. 5).
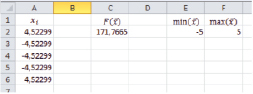
Рис. 5. Оптимизация методом ОПГ решения, полученного иммунным алгоритмом
Таким образом, наиболее точным и окончательным решением является новая точка
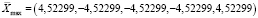, при этом 
.
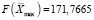Найдём отклонение между решением, полученным при помощи комбинированного алгоритма, и решением, найденным иммунной системой. Вектор отклонения координат между этими точками будет следующим.
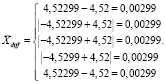
Также можно легко посчитать разницу между целевыми функциями.
Fdiff = 171,7665 – 171,7577 = 0,0088.
Заключение
Целью проведённого исследования являлся анализ скорее качественных, нежели количественных свойств сцепки детерминированных и стохастических алгоритмов. Поэтому был использован ряд упрощений и допущений. Очевидно, что на описанной задаче при увеличении параметра точности иммунной системы она способна самостоятельно показать полноценное решение, не нуждающееся в дальнейшей оптимизации. Целевая функция с пятью переменными слишком проста для того, чтобы решать её при помощи эвристического алгоритма, которые применяют на мерностях, кратных десяткам и сотням. Однако такую функцию легко использовать, описывать и представлять в удобочитаемом виде. При увеличении требуемой точности эвристический алгоритм будет работать всё медленнее, что серьёзно скажется в случае крупномасштабных задач. Поэтому если размерность целевой функции по-настоящему велика, то для её решения потребуется огромное количество особей, с которыми работает эвристика (будь то гены в генетических алгоритмах или клетки в иммунных). Тогда, для ускорения процесса решения потребуется снижение точности, и результат получится крайне приближённым. В этом случае и понадобится дополнительное использование детерминированных методов для улучшения приближённого решения и превращения его в точное.
Тем не менее данное исследование показывает, как можно использовать комбинацию двух противоположных классов методов оптимизации для оптимизации такой целевой функции, которую ни один из описанных алгоритмов самостоятельно решить не смог. В реальности на задачах с десятикратными размерностями такая комбинация будет приносить очень ощутимый результат благодаря взаимному дополнению описанных классов алгоритмов и взаимной компенсации их слабых сторон.
Статья написана при поддержке гранта РФФИ № 16-01-00391 «Разработка комбинированных алгоритмов для решения распределительных и транспортных задач с использованием идеологии искусственных иммунных систем и биоинспирированных алгоритмов».