Наличие упругого тягового органа в рассматриваемой системе электропривода, с одной стороны, существенно ухудшает режим работы электромеханической установки, а с другой – делает весьма сложной математическую модель, необходимую для оптимизации системы управления. Описывая механическую часть электропривода, нужно рассматривать ее как многомассовую упругую систему. Здесь наибольшие затруднения возникают при получении аналитической зависимости перемещений и усилий в отдельных сечениях тягового органа.
Как показал опыт многочисленных исследований подобных одноприводных систем, элементарной схемой является схема, представленная на рис. 1, а. Все другие представляют определенное сочетание таких элементарных схем. Для описания динамики таких систем предложен ряд методов.
Рассмотрим некоторые методы и оценим их с точки зрения эффективности их применения для решения задачи оптимизации управления многодвигательным электроприводом.
Метод граничных упругих связей
Данный метод, предложенный в [1], состоит в том, что в места соединения (или прижатия) тягового органа к сосредоточенным массам вводятся вспомогательные идеальные упругие связи с коэффициентом жесткости Ск (в окончательных аналитических зависимостях вспомогательные связи исключаются), рис. 1, б.
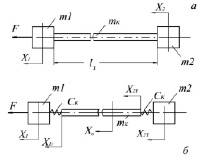
Рис. 1. Расчетные схемы двухмассовых систем с инертной упругой связью
Тогда усилия, действующие со стороны тягового органа на сосредоточенные массы, будут равны
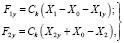(1)
где X1y, X2y – перемещения крайних сечений относительно центра тяжести отрезка тягового органа длиной l1; X0 – перемещение тягового органа как абсолютно твердого тела. Чем больше коэффициент Ск, тем меньше разности X1 – X0 – X1y и X2y + X0 – X2.
Искусственное отделение тягового органа от сосредоточенных масс позволяет рассматривать систему как состоящую из трех взаимосвязанных звеньев с определенными входными и выходными переменными (рис. 2).
Принимая упругие силы F1y и F2y направленными от сосредоточенных масс m1 и m2 звенья 1 и 2 будут описываться уравнениями
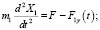(2)
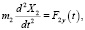(3)
где F = F(t) – динамическая составляющая усилия приложенного в массе m1, F = FДВ – FСТ, FСТ – сила статических сопротивлений движению системы, FДВ – сила создаваемая двигателем. Для описания звена нужно в общем случае рассматривать его как звено с распределенными параметрами (массой упругостью). Наиболее близкой аналогией является упругий стержень со свободными концами, к которым приложены силы F1y
и F2y. В системах такого вида для определения перемещения любого поперечного сечения тягового органа длиной l1 без учета рассеивания энергии необходимо решить волновое уравнение
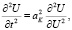(4)
где aK – скорость распространения в продольном направлении упругих деформаций, м/с.
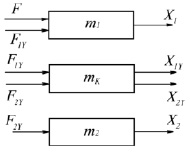
Рис. 2. Декомпозиция двух массовой упругой системы
Для свободных колебаний в случае одновременного действия сил F1y и F2y изображения перемещений крайних сечений принимают вид [2, 3]:
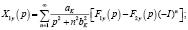(5)
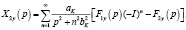. (6)
Из равенства (7) следует важный вывод, что если рассматривать колебания относительно перемещения тягового органа как абсолютно твердого тела, описываемого уравнением
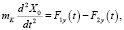(7)
то можно учитывать только нечетные члены рядов [4, 5].
Тогда уравнения (5) и (6) запишутся так:
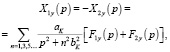(8)
где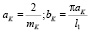 
– коэффициент учитывающий моменты инерции движущих звеньев; mK – масса ветви тягового органа длиной l1.
Учитывая, что многодвигательный электропривод благодаря большим сосредоточенным массам является фильтром низкочастотных колебаний, а также принимая тяговый орган как упруго-вязкий стержень, зависимость (8) запишется выражением
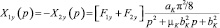. (9)
Составленная по уравнениям (1), (2), (3), (7) и (9) структурная схема по отношению к динамическим усилиям F1y и F2y, после исключения вспомогательных упругих связей (подставляется Ск = ∞) будет иметь вид, показанный на рис. 3.
Передаточные функции по отношению к F1y и F2y:
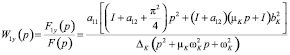; (10)
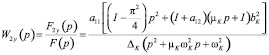; (11)
где
; 
;
; 
;
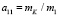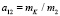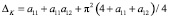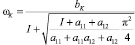μK – коэффициент сопротивления.
Структурная схема определения усилий в переменных состояния приведена на рис. 4.
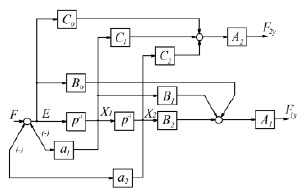
Рис. 4. Схема упругой системы в переменных состояния
На этой схеме:
.
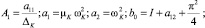
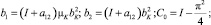
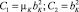Переменные состояния системы связаны с величиной Е следующими зависимостями:
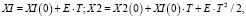
где XI и X2 – значения переменных на N-ом шаге интегрирования;
XI (0) и X2 (0) – значения этих переменных, полученные на предыдущем шаге.
где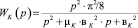 
.
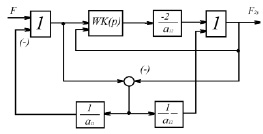
Рис. 3. Структурная схема упругой системы
Укрупненная структурная схема алгоритма определения усилий F1y и F2y приведена на рис. 4.
Ориентировочную оценку переходного процесса можно дать непосредственно по изображениям (10) и (11). Так, кроме частоты колебаний ωK, можно, не прибегая к исследованию процесса, определить начальные и установившиеся значения F1y и F2y.
При p → 0 и t = 0
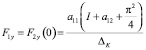
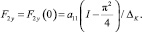
При p → 0 и t = 0
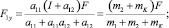
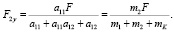
Замещение упругой системы с распределенными параметрами дискретной цепной системой
Как показано в [6], упругую систему с распределенными массой и упругостью можно заменить системой с сосредоточенными массами, соединенными упругими идеальными связями, как показано на рис. 5, а.
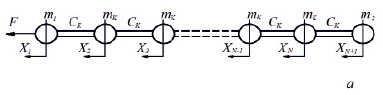
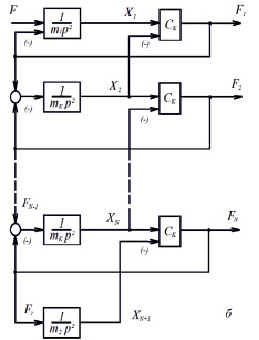
Рис. 5. Расчетная (а) и структурная (б) схемы многомассовой упругой системы
Чем больше число участков N, тем ближе по динамическим свойствам дискретная система системе с распределенными параметрами. Общий коэффициент жесткости упругого тягового органа Сy можно определить по скорости распространения упругой деформации aK:
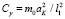. (12)
Разделив участок тягового органа, расположенный между сосредоточенными массами m1 и m2, N частей и приравняв элементарную сосредоточенную массу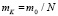 
, найдем коэффициент жесткости элементарной упругой связи CK из равенства
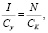откуда CK = N?Cy.
В каждую из масс m1 и m2 включены половины масс mK. Обозначив собственные сосредоточенные массы m10 и m20, будем иметь:
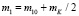и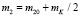 
.
Следовательно, согласно принятым
выше обозначениям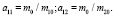 
Запишем систему уравнений динамики упругой системы (рис. 5, а) при ступенчатом приложении усилия F.
.
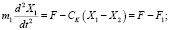
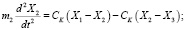
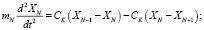
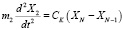Данным уравнениям соответствует структурная схема (рис. 5, б), которую можно упростить, заменив абсолютные значения сосредоточенных масс относительными величинами (рис. 6). Нормированные коэффициенты a1, a2 и βK равны
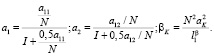(13)
По полученной нормированной структурной схеме легко составляются уравнения состояния и алгоритм анализа переходных процессов для любого числа участков N. Примем N = 6 и значения параметров системы a 11 = 0,5; a12 = 2; aK = 4000; l1 = 1500; F = 200 кН. Уравнения динамики относительно действительных упругих усилий и фиктивных переменных y1 и dy1/dt = V1:
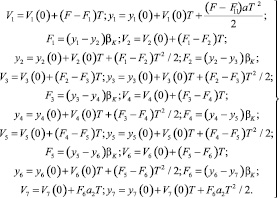(14)
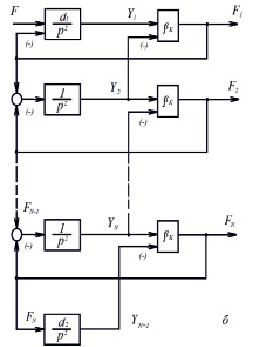
Рис. 6. Универсальная схема многодвигательной упругой системы
Структурная схема алгоритма определения усилий Fi в функции времени приведена на рис. 7.
Графики F1(t) и F2(t) – рис. 8, а, б. На рисунках для сравнения показаны графики усилий F1y и F2y, полученные по формулам (10) и (11). На рис. 8, в приведены графики F1y(t) и F2y(t) при коэффициенте демпфирования μK, рав-
ном 0,01.
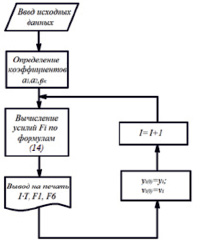
Рис. 7. Структурная схема алгоритма определения упругих сил в многомассовых системах
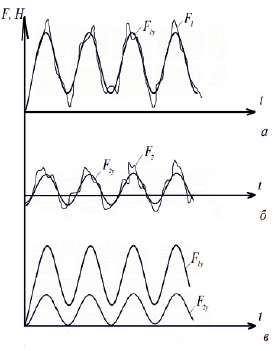
Рис. 8. Графики упругих сил, полученные на ЭВМ
В настоящее время предлагается снижение динамических нагрузок с помощью специальной задающей модели [7], где можно рассматривать наиболее сложную в динамическом отношении систему – установку со шкивами трения. В качестве тягового органа могут использоваться стальные канаты или резино-тросовые ленты.