Мультипроектное планирование (RCMPSP – resource-constrained multi-project scheduling problem) решает взаимосвязанные проблемы – формирование календарного графика и распределение ресурсов. В большинстве исследований установлена NP-трудность задач мультипроектного планирования и, как следствие, необходимость нахождения эвристик, понижающих порядок операций полного перебора. Основой эвристических подходов является использование схем формирования расписаний (SGS – schedule generation scheme) и правил приоритетов (PR – priority rules) [5, 10]. Приоритетами в этом контексте выступают критерии для определения очередности выполнения (включения в календарный график) конкурирующих по ресурсам работ (проектов). Критерии являются скалярными величинами разных характеристик заявок/работ и проектов, включая выделяемые и требуемые ресурсы. Под правилами приоритетов понимаются определенные последовательности приемов и методов определения очередности выполнения (включения в календарный график) конкурирующих по ресурсам работ (проектов). Правила приоритетов используют однокритериальное ранжирование скалярных величин приоритетов, что обусловлено потребностями «ручного» планирования, по крайней мере на предварительном этапе. Большое количество критериев, используемых в качестве приоритетов [5, 6, 7, 9, 10], свидетельствует о многокритериальном характере проблемы и отсутствии нужных решений. В одной из немногих работ [9] представлено более сложное ранжирование характеристик проектов с помощью метода анализа иерархий.
Целью статьи является представление подходов к использованию методов ранжирования в программном формировании календарного графика для произвольного количества проектов в системе с ограниченными ресурсами.
По способу применения приоритеты разделяются на приоритеты для планирования одного проекта (RCPSP – resource-constrained project scheduling problem) и приоритеты мультипроектного планирования [5].
К приоритетам RCPSP относятся:
– FCFS – First Come First Served – работа с минимальным номером обслуживается (включается в календарный график) первой;
– LCFS – Last Come First Served – работа с максимальным номером обслуживается первой;
– SOF – Shortest Operation First – кратчайшая операция обслуживается первой;
– MOF – Maximum (longest) Operation First – наиболее продолжительная операция обслуживается первой;
– RAN – Random – случайный выбор операции проекта;
– EDDF – Earliest Due Date First – первой обслуживается операция с самым ранним началом;
– MAXSP – Maximum Schedule Pressure – первой обслуживается операция с максимальным давлением;
– MINLFT – Minimum Late Finish time – первой обслуживается операция с минимальным временем окончания;
– MINWCS – Minimum Worst Case Slack – минимальный худший резерв;
– WACRU – Weighted Activity Criticality & Resource Utilization – взвешенная критичность операции и использования ресурсов;
– MS – Maximum Total Successors – максимальное число последователей;
– MCS – Maximum Critical Successors – максимальное число критичных последователей.
К приоритетам RCMPSP относятся:
– MINSLK – Minimum Slack – минимальный резерв;
– MAXSLK – Maximum Slack – максимальный резерв;
– SASP – Shortest Activity from Shortest Project – кратчайшая операция из кратчайшего проекта обслуживается первой;
– LALP – Longest Activity from Longest Project – самая длительная операция из самого длительного проекта обслуживается первой;
– MINTWK – Minimum Total Work content – выбор операции, дающей минимальный объем потребления ресурсов;
– MAXTWK – Maximum Total Work content – выбор операции, дающей максимальный объем потребления ресурсов;
– TWK-LST – MAXTWK & earliest Late Start time (2-phase rule) – первоначальная приоритизация по MAXTWK, затем по наиболее раннему позднему началу операции (двухфазное правило);
– TWK-EST – MAXTWK & earliest Early Start time (2-phase rule) – первоначальная приоритизация по MAXTWK, затем по наиболее раннему раннему началу операции (двухфазное правило).
На предварительном этапе планирования правила приоритетов используются для формирования начальных решений (календарных графиков проектов или мультипроектов) [1, 5, 10], к которым применяются оптимизирующие эвристики. На этапе оптимизации календарных графиков правила приоритетов встраиваются в соответствующие эвристики [6, 7, 9]. Различные исследования не дали однозначного предпочтения какому-либо критерию применительно к мультипроектному планированию [5, 7, 9].
При исследовании систем различного рода используются критерии с векторными и многовекторными компонентами. Задачи принятия решений в этом случае сводятся к задачам многокритериального, многовекторного и гипервекторного ранжирования.
Для однозначного понимания терминологии введем следующие определения [4]:
- многокритериальным ранжированием является ранжирование векторных критериев, представляющих собой упорядоченные множества скалярных компонент (рис. 1). По мнению авторов данной статьи, наиболее адекватным многокритериальным ранжированием является «жесткое» ранжирование [4]. Будут различаться прямое (по «возрастанию») и обратное (по «убыванию») многокритериальное ранжирование;
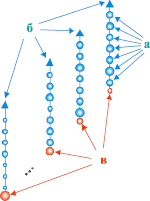
Рис. 1. Многокритериальное ранжирование: а – скалярные компоненты вектора; б – ранжируемые векторы; в – ранги векторов
- многовекторным ранжированием является ранжирование критериев, представляющих собой упорядоченные множества векторных компонент, а каждая векторная компонента – упорядоченное множество скалярных компонент (рис. 2). Многовекторное ранжирование n критериев с k векторными компонентами (рис. 2, а) осуществляется следующим образом: первоначально производится k «жестких» ранжирований соответствующих векторных компонент (рис. 2, б) с формированием рангов (рис. 2, в); затем «жестко» ранжируются n векторов рангов (рис. 2, г) с формированием рангов (рис. 2, д);
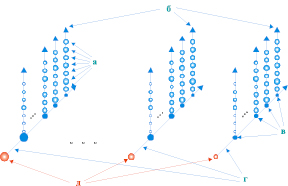
Рис. 2. Многовекторное ранжирование: а – скалярные компоненты вектора; б – ранжируемые векторы; в – ранги векторов; г – ранжируемые многовекторные компоненты; д – ранги многовекторных компонент
- гипервекторное ранжирование является ранжированием критериев, представляющих собой упорядоченные множества многовекторных компонент, каждая многовекторная компонента – упорядоченное множество векторных компонент, а каждая векторная компонента – упорядоченное множество скалярных компонент (рис. 3). Гипервекторное ранжирование m гипервекторных критериев, каждый из которых содержит n многовекторных критериев с k векторными компонентами, осуществляется следующим образом: первоначально производится k «жестких» ранжирований соответствующих векторных компонент (рис. 3, б) с формированием рангов (рис. 3, в); затем производится n «жестких» ранжирований соответствующих векторов рангов многовекторных компонент (рис. 3, г) с формированием рангов (рис. 3, д); затем «жестко» ранжируются m векторов рангов гипервекторных компонент (рис. 3, е) с формированием рангов (рис. 3, ж).
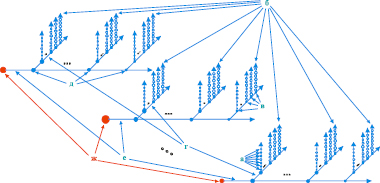
Рис. 3. Гипервекторное ранжирование: а – скалярные компоненты вектора; б – ранжируемые векторы; в – ранги векторов; г – ранжируемые многовекторные компоненты; д – ранги многовекторных компонент; е – ранжируемые гипервекторные компоненты; ж – ранги гипервекторных компонент
Для мультипроектного планирования предложены две последовательно применяемые схемы: SGS1 – формирование начального календарного графика; SGS2 – его последующая оптимизация [2].
В каждом цикле SGS1 используются два взаимосвязанных правила приоритетов PR11 и PR12. Стратегия PR11 связана с выбором наиболее загруженного по требуемым ресурсам проекта среди не включенных в начальный календарный график. Для проекта выбранного правилом PR11 в правиле PR12 определяется время начала выполнения в начальном календарном графике с обеспечением наибольшей равномерности потребления ресурсов.
В каждом цикле SGS2 также используются два взаимосвязанных правила приоритетов PR21 и PR22. Стратегия PR11 связана с выбором наиболее неравномерного по потреблению ресурсов в календарном графике проекта. Для проекта выбранного правилом PR21 в правиле PR22 определяется время начала выполнения в интервале расписания по крайней мере не ухудшающее интегральную оценку равномерности (критерий равномерности) всего графика.
Для численных экспериментов использовалось тестовое задание, включающее 15 проектов, случайно выбранных из библиотеки тестовых задач PSPLib [8]. Проекты включают по 30 заявок работ, каждой из которых требуется до 4 типов ресурсов в течение их выполнения. Инициируемая заявкой работа характеризуется своей длительностью в тактах планирования. Внутри проекта заявки связаны отношениями предшествования/следования.
Рассмотрим использование правила приоритетов PR11 для ситуации, в которой проекты 12 и 7 уже включены в начальный календарный график. Критерии загруженности проектов формируются на основе скалярных оценок загруженности заявок по каждому из четырех ресурсов. Оценка загруженности определяется произведением тактовой потребности заявки в ресурсе на длительность выполнения работы заявки [2, 3], что позволяет представить каждую заявку вектором из четырех скалярных оценок, упорядоченных по ресурсам. Обратное многокритериальное ранжирование векторов загруженности заявок формируют ранги заявок, определяющие критерии (векторы) загруженности путей графов проектов. Прямое многокритериальное ранжирование векторов загруженности путей графов проектов определяет их ранги, которые формируют критерии (векторы) загруженности проектов. Прямое многокритериальное ранжирование векторов загруженности проектов определяет доминирующий проект, который и будет самым загруженным. Таким образом, правило PR11 реализует гипервекторное ранжирование приоритетов, представленных критериями загруженности проектов.
Таблица 2
Результаты ранжирования для 10 наиболее загруженных путей графов проектов
|
№ проекта |
Путь _ID |
Отсортированные по возрастанию ранги заявок путей графов проектов |
Ранг пути |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||
|
9 |
162 |
2 |
6 |
21 |
94 |
176 |
263 |
273 |
296 |
318 |
1 |
|
9 |
161 |
2 |
6 |
21 |
86 |
179 |
263 |
273 |
296 |
318 |
1 |
|
5 |
84 |
8 |
12 |
26 |
43 |
103 |
115 |
1000 |
1000 |
1000 |
2 |
|
11 |
204 |
40 |
44 |
63 |
78 |
88 |
177 |
261 |
1000 |
1000 |
3 |
|
13 |
248 |
14 |
35 |
77 |
82 |
168 |
234 |
254 |
1000 |
1000 |
4 |
|
5 |
86 |
8 |
25 |
26 |
115 |
148 |
274 |
322 |
358 |
1000 |
5 |
|
13 |
251 |
14 |
35 |
36 |
77 |
204 |
283 |
1000 |
1000 |
1000 |
6 |
|
13 |
250 |
48 |
60 |
82 |
106 |
234 |
237 |
254 |
333 |
1000 |
7 |
|
13 |
249 |
48 |
60 |
89 |
106 |
225 |
237 |
254 |
333 |
1000 |
8 |
|
13 |
252 |
14 |
35 |
77 |
204 |
234 |
254 |
283 |
1000 |
1000 |
9 |
|
10 |
182 |
3 |
59 |
62 |
121 |
185 |
297 |
306 |
1000 |
1000 |
10 |
В табл. 2 представлены выборочные результаты ранжирования векторов загруженности путей графов проектов в очередном цикле формирования начального календарного графика. Так как эти векторы имеют разную размерность, то для их многокритериального ранжирования значениям недостающих скалярных компонент необходимо присвоение фиктивных значений. В зависимости от решаемой задачи в качестве таких значений присваиваются:
- минимально возможное значение при обратном ранжировании;
- максимально возможное значение при прямом ранжировании.
Графы проектов тестового задания имеют суммарно 356 векторов путей, поэтому значениям недостающих скалярных компонент (табл. 2) присвоено значение 1000.
Реализация правила PR11 (гипервекторное ранжирование критериев загруженности проектов) определила проект 5 (табл. 1) в рассматриваемой ситуации наиболее загруженным проектом. С помощью правила PR12 (многовекторное ранжирование критериев равномерности проектов) проект 5 включается в начальный календарный график, после чего осуществляется переход к следующему циклу схемы SGS1.
Таблица 1
Характеристики проектов тестового задания
|
№ проекта |
Обозначение проекта |
Код генератора |
Выделяемые проекту ресурсы на такт планирования |
Критический путь, такты планирования |
|||
|
R1 |
R2 |
R3 |
R4 |
||||
|
1 |
j30_28.bas |
1350739460 |
42 |
39 |
51 |
44 |
47 |
|
2 |
j30_28.bas |
1001619525 |
28 |
40 |
43 |
39 |
63 |
|
3 |
j30_29.bas |
1768635613 |
19 |
17 |
20 |
19 |
44 |
|
4 |
j30_29.bas |
1037926147 |
17 |
15 |
17 |
17 |
51 |
|
5 |
j30_29.bas |
401731488 |
15 |
14 |
16 |
16 |
48 |
|
6 |
j30_30.bas |
677072906 |
30 |
28 |
26 |
33 |
34 |
|
7 |
j30_30.bas |
712413196 |
23 |
23 |
22 |
20 |
44 |
|
8 |
j30_28.bas |
890933679 |
28 |
25 |
34 |
42 |
46 |
|
9 |
j30_31.bas |
1335687044 |
32 |
26 |
25 |
32 |
48 |
|
10 |
j30_31.bas |
2012720068 |
23 |
25 |
28 |
30 |
46 |
|
11 |
j30_31.bas |
1594625014 |
34 |
41 |
46 |
37 |
48 |
|
12 |
j30_31.bas |
670867861 |
24 |
30 |
25 |
25 |
56 |
|
13 |
j30_32.bas |
1264544214 |
29 |
39 |
51 |
43 |
48 |
|
14 |
j30_41.bas |
377662011 |
18 |
13 |
16 |
14 |
45 |
|
15 |
j30_41.bas |
1980474781 |
13 |
14 |
12 |
13 |
48 |
Таким образом, получены следующие результаты:
- для решения задач формирования календарных графиков мультипроектного планирования представлены две схемы генерации расписаний с использованием правил приоритетов, реализующих методы ранжирования теории принятия решений;
- показаны результаты гипервекторного ранжирования критериев загруженности проектов.



